Algorytmy genetyczne...
Czym są 'algorytmy genetyczne'?...Najprościej rzecz ujmując jest to próba zasymulowania w pamięci komputera populacji jakiegoś gatunku. Na taką populację składają się dziesiątki, setki, tysiące... pojedynczych osobników. Osobniki te między sobą mogą się krzyżować, mogą również następować jakieś samoistne zmiany w strukturze pojedynczego osobnika (tzw. mutacja). W wyniku krzyżowania i mutacji powstają nowe osobniki. Ze względu na fakt, że populacja ma swój z góry narzucony maksymalny rozmiar część osobników należy z niej usunąć (ten krok nazywany jest selekcją). Oczywiście usuwane są te najmniej przystosowane... Cały ten proces (krzyżowanie, mutacja, selekcja) powtarzany jest w nieskończoność...
Powyższy opis dotyczył komputerowych algortymów, ale na pierwszy rzut oka widać ogromną analogię do matki natury (krzyżowania chyba nie muszą tłumaczyć, mutacja może być spowodowana np. Czarnobylem, a selekcji może dokonywać wilk który szybciej dogoni słabszą sarenkę...). I to chyba ona była wzorem dla twórców algorytmów genetycznych...
Cóż z algorytmów genetycznych jest dobrego dla kodera, a tym bardziej dla sztucznej inteligencji?...
Przyjmnijmy, że mamy do rozwiązania 'problem komiwojażera' (krótka definicja tego zagadnienia: komiwojażer ma do odwiedzenia n miast, wszystkie są ze sobą połączone (oznacza to że z każdego komiwojażer może dojechać do wszystkich pozostałych). Należy znaleźć najkrótszą drogę jaką musi pokonać komiwojażer). W przypadku małej ilości miast problem wydaje się być łatwy. Wystarczy zestawić wszystkie permutacje miast, obliczyć otrzymane w ten sposób odległości i wybrać najkrótszą. Jednak problem komiwojażera jest NP-trudny (oznacza to że przy wzroście rozmiaru instancji (liczby miast) czas potrzeby na obliczenia rośnie wykładniczo (w przypadku problemu komiwojażera dodanie jednego miasta powoduje dwukrotne zwiększenie czasu obliczeń)) dlatego ten sposób rozwiązania na dłuższą metę jest niefajny...
Zaprzągnijmy więc do roboty algorytmy genetyczne. Jako 'gatunek' możemy przyjąć trasę komiwojażera. Każdy osobnik będzie pamiętał jedną trasę. Takich osobników może być dowolna ilość (im więcej tym bardziej zróżnicowana populacja jednak kosztem dłuższych obliczeń). Na początku do każdego osobnika wpisujemy trasę zupełnie losową... I rozpoczynamy algorytm genetyczny. Krzyżowanie polega na wymianie pomędzy dwoma osobnikami pewnych elementów tras (czyli podtras), natomiast mutacja może oznaczać wymianę w pojedynczym osobniku dwóch miast między sobą. Jeśli dodamy do tego krok selekcji, czyli wybór do następnej populacji osobników najlepiej przystosowanych (to znaczy takich które reprezentują trasy o najmniejszym koszcie) otrzymamy algorytm, który po pewnej liczbie kroków znajdzie nam całkiem niezłą trasę przez wszystkie miasta...
Niestety algortymy genetyczne są tylko heurystyką. Oznacza to, że otrzymane rozwiązania nie zawsze będą najlepszymi możliwymi. W zamian za to otrzymujemy rozwiązania bardzo dobre w rozsądnym czasie.
Algorytmy genetyczne rozłożone na elementy pierwsze...
Szczegółowy opis elementów algorytmu genetycznego powinniśmy rozpocząć od opisu najmniejszego elementu algorytmu, czyli od opisu pojedynczego osobnika.W zasadzie jest to jedyny element w algorytmie, który jest różny w przypadku różnego wykorzystania algorytmów. Dlatego projektowanie osobnika jest chyba najważniejszą częścią projektowania całego algorytmu genetycznego. Ze względu na niepowtarzalność gatunku trudno jest zdefiniować 'złotą zasadę' projektowania osobnika. W tym miejscu mogę podać jedynie kilka cech, które tworzony przez nas gatunek powinien spełniać.
Przede wszystkim należy pamiętać, że w algorymie genetycznym bierze udział bardzo wiele osobników (kilkadziesiąt/set/tysięcy), dlatego ważną cechą osobnika jest długość jego reprezentacji. Wiadomo, że liczba osobników jest sztywno ograniczana liczbą dostępnej pamięci (komputera), dlatego im mniejsza będzie reprezentacja gatunku tym więcej osobników będzie mogło brać udział w ewolucji (a co za tym idzie większe będą szanse znalezienia globalnego optimum). Poza tym inne elementy algorytmu (krzyżowanie, mutacja...), będą działać dużo szybciej gdy poszczególne osobniki będą miały mniejszą wielkość.
I od razu mały przykładzik. Przyjmijmy, że naszym gatunkiem jest homo sapiens charakteryzujący się następującymi cechami:
Płeć (kobieta / mężczyzna)
Kolor oczu (mamy do wyboru: niebieskie, piwne, brązowe i czarne)
Wzrost (poniżej 140, 140-150, 150-160, 160-170, 170-180, 180-190, 190-200, powyżej 200)
Narodowość (mamy do wyboru: Polak, Niemiec, Czech, Rosjanin)
Najprosztrzą reprezentacją homo sapiensa wydaje się być struktura w której będą zapamiętywane wartości poszczególnych atrybutów. Jeśli na każdy atrybut przeznaczymy zmienną typu char* (string) to otrzymamy całkiem pokaźny rozmiar osobnika. Dodatkową wadą takiej reprezentacji jest dostyć duża niewygoda krzyżowania i mutacji (o której będzie mowa za chwilę). Niewątpliwą zaletą tej reprezentacji jest jest 'bezpośredniość', wszystkie pola struktury pamiętają konkretną wartość atrybutu. Celem zmniejszenia rozmiaru struktury można przyjąć, że dla przechowywania wartości atrybutów wykorzystane zostaną zmienne liczbowe (int, byte...) wtedy rozmiar naszej struktury opisującej człowieka zmniejszy się do 4 bajtów. W tym wypadku nie będziemy mieli w strukturze natychmiastowej informacji o wartościach atrybutów i w związku z tym należy stosować pewne oznaczenia. Np: dla płci 0 oznacza kobietę, 1 oznacza mężczyznę, dla koloru oczu 0 oznacza niebieskie, 1 oznacza piwne, 2 oznacza brązowe, 3 oznacza czarne. Reprezentacja ta jest już niewielka i całkiem wygodna w późniejszej obsłudze. Można się jednak w opisie homo sapiensa posunąć trochę dalej i wykorzystać reprezentację bitową. Proszę zauważyć, że do reprezentacji płci wystarczy jeden bit (wartość zero-kobieta, jeden-mężczyzna), do reprezentacji koloru oczu dwa bity (00-niebieskie, 01-piwne, 10-zielone, 11-czarne), do reprezentacji wzrostu też trzy bity, a do reprezentacji narodowości dwa bity. I w przypadku takiego kodowania wartości wszystkich atrybutów mieszczą się w 8 bitach. Te 8 bitów tworzą całkowity obraz pojedynczego osobnika. Przy tej reprezentacji należy na początku przyjąć w jakiej kolejności poszególne atrybuty będą występowały w reprezentacji osobnika. W naszym przypadku przyjmijmy, że pierwszy bit będzie informował o płci następne o kolorze oczu, wzroście i narodowości. Dla przykładu chromosom: 00000000 reprezentuje niebieskooką Polkę o wzroście nieprzekraczającym 140cm, a chromosom 11011001 reprezentuje wysokiego (190-200) Niemca o brązowych oczach.
I jeszcze jeden przykładzik pokazujący jak można stworzyć binarną reprezentację liczb naturalnych. Przyjmijmy, że mamy do rozwiązania problem znalezienia takiego x'a dla którego funkcja postaci y=f(x) ma minimum (maksimum). Szukamy po prostu ekstremów funkcji. W tym przypadku pojednycze rozwiązanie ma reprezentować pojedynczą wartości x'a. Można do tego celu użyć zmiennej typu float (real), jednak wtedy trudno jest wymyśleć jakiś rozsądny sposób krzyżowania takich osobników. Innym wygodniejszym sposobem kodowania x'ów jest zastosowanie reprezentacji bitowej. W tym wypadku tracimy jednak na maksymalnej rozdzielczości. Dla przykładu jeśli badamy funkcję w przedziale 1-3 i reprezentujemy x'y na 4 bitach to otrzymujemy maksymalną rozdzielczość:
(max_x-min_x)/(2^(liczba_bitów)-1)=(3-1)/(2^4-1)=2/15=0.1333
Oznacza to, że najmniejsza możliwa różnica pomiędzy analizowanymi x'ami jest równa 0,13333. Następujące wartości bitów odpowiadają następującym wartościami x'a:
0000-1.0
0001-1.1333
0010-1.2666
0011-1.4 itd.
Jeśli mamy już zaprojektowany chromosom (krótki i wygodny w obsłudze) możemy zająć się samym algorytmem. W uproszczeniu wygląda on następująco:
1. Losowanie populacji
2. Ocena osobników
3. Selekcja
4. Krzyżowanie
5. Mutacja
6. Powrót do punktu 2
Poniżej opis poszczególnych jego elementów:
Losowanie populacji
W tym miejscu należy ustalić jak wielka będzie tworzona populacja. Jeśli populacja będzie zawierała zbyt mało osobników to algorytm może zatrzymać się w jakimś minimum lokalnym (gdy jakieś niezłe (ale nie najlepsze) rozwiązanie zdominuje całą populację). Z drugiej strony zbyt duża liczebność populacji zmniejsza szybkość działania algorytmu. Po ustaleniu wielkości populacji należy stworzyć wszystkie osobniki. Ze względu na fakt, że początkowa populacja powinna być jak najbardziej różnorodna każdy osobnik powinien być tworzony całkowicie losowo. W tym miejscu widać przewagę reprezentacji bitowej gdzie bez względu na rodzaj problemu nowo tworzony osobnik zawiera n losowo wygenerowanych bitów. W przypadku reprezentacji osobnika w strukturze należy każde jej pole wypełnić osobno. Na tym kroku należy pamiętać aby tworzone osobniki były poprawne to znaczy reprezentowały obiekty należące do dziedziny problemu. Np przy tworzeniu x'ów (problem znajdowania ekstremum) w przedziale 1-3 wygenerowany chromosom nie może reprezentować x'a o wartości np. 5. W przypadku reprezentacji bitowej ten problem pojawia się wtedy gdy do reprezentowania jakiegoś atrybutu nie są wykożystywane wszystkie kombinacje bitów. Wracając do poprzedniego przykładu chromosomu opisującego homo sapiensa, jeśli nie uwzględnialibyśmy Rosjan to chromosom 000000011 nie byłby poprawny.
Ocena osobników
W tym kroku banana jest 'dobroć' poszczególnych osobników. W zależności od rodzaju problemu różne są funkcje sprawdzające przystosowanie osobników. W przypadku ekstremum funkcji 'dobrocią' jest po prostu wartość funkcji w zadanym x'ie. W przypadku rozwiązywania problemu komiwojażera jest to długość trasy jaka jest reprezentowana przez danego osobnika. W tym miejsu można wprowadzić tzw. funkcję kary za niedopuszczalne rozwiązanie. Wcześniej wspomniałem, że o poprawne osobniki należy zadbać podczas tworzenia populacji (niepoprawne osobniki mogą też powstawać w krokach krzyżowania i mutacji). Czasmami jest to jednak trudne do wykonania dlatego przy losowaniu można te osobniki zaakceptować a w tym kroku dodać funkcję kary. Spowoduje ona dużo mniejsze prawdopodobieństwo przejścia przez danego osobnika kroku selekcji. W zależności od tego czy funkcję dopasowania ('dobroć') minimalizujemy czy maksymalizujemy wartość funkcji błędu należy do niej dodać bądź odjąć.
Selekcja
Krok ten jest esensją całej genetyki. W tym miejscu tworzona jest nowa populacja na podstawie już istniejącej. W zależności od wartości funkcji oceny (obliczanej w poprzednim kroku) dany osobnik ma większe (gdy jest 'dobry') lub mniejsze (gdy jest 'słaby') szanse na znalezienie się w kolejnym pokoleniu. Istnieje kilka sposobów obliczania 'szansy' poszczególnych osobników:
Koło ruletki - Polega na n krotnym losowaniu (n - liczba osobników w populacji) ze starej populacji osobników, które zostaną przepisane do nowej populacji. Oczywiście wszystkie osobniki mają różne prawdopodobieństwa wylosowania. Prawdopodobieństwo to jest liczone z następującego wzoru:
Wartość przystosowania danego osobnika/suma wartości przystosowania wszystkich osobników
Powyższy wzór jest poprawny tylko wtedy gdy maksymalizujemy funkcję oceny. Gdybyśmy ją minimalizowali można zastosować następujący wzór:
(Wartość najgorszego osobnika-Wartość danego osobnika+1)/(suma wartości wszystkich osobników+1)
Wzór ten odwraca minimalizację na maksymalizację.
I od razu mały przykład (przyjmijmy maksymalizację funkcji przystosowania). Mamy trzy osobniki o następujących wartościach przystosowania: 5,1,2. Odpowiadające im wartości prawdopodobieństwa są zatem równe:
* Pierwszy osobnik: 5/8, czyli 62,5%
* Drugi osobnik: 1/8, czyli 12,5%
* Trzeci osobnik: 2/8, czyli 25%
Ranking liniowy - Selekcja tą metodą jest bardzo podobna do selekcji metodą koła ruletki. Modyfikacja polega jedynie na zmianie funkcji określającej prawdopodobieństwo wyboru danego osobnika. Przed przystąpieniem do tej selekcji należy nadać każdemu z osobników pewną wartość (przystosowanie) zależną od jego położenia na liście posortowanej względem wartości funkcji oceny. Jeśli chcemy maksymalizować to wartości powinny być posortowane rosnąco, w przypadku minimalizacji wartości powinny być posortowane malejąco. Aby obliczyć prawdopodobieństwo wybrania każdego osobnika można skorzystać ze wzoru:
Prawdopodobieństwo=Przystosowanie/Suma przystosowania wszystkich osobników
Dla powyższego przykładu wartości prawdopodobieństw wyglądałyby następująco:
* Pierwszy osobnik: 3/6, czyli 50%
* Drugi osobnik: 1/6, czyli 16,7%
* Trzeci osobnik: 2/6, czyli 33,3%
Ten sposób wyliczania prawdopodobieństw zmniejsza przewagę jaką mają najlepsze rozwiązania, gdy ich przewaga jest b.duża i zwiększa przewagę gdy jest ona b.mała.
Turniej - Metoda jest zupełnie różna od powyższych i polega na losowym wyborze z całej populacji kilku osobników (jest to tzw. grupa turniejowa), a później z tej grupy wybierany jest osobnik najlepiej przystosowany i on przepisywany jest do nowo tworzonej populacji. Losowanie grup turniejowych oraz wybieranie z nich najlepszego osobnika należy powtórzyć aż do utworzenia całej nowej populacji.
Selekcja metodą turniejową jest pozbawiona niedogodności metody koła ruletki, gdzie wymagana jest maksymalizacja funkcji oceny, w turnieju ważna jest jedynie informacja o 'lepszości' jednego rozwiązania nad innym.
Krzyżowanie
Zadaniem kroku krzyżowania jest wymiana "materiału genetycznego" pomiędzy dwoma rozwiązaniami w populacji. W wyniku krzyżowania na podstawie dwóch rozwiązań (rodzice) tworzone są dwa nowe osobniki (dzieci). Po wykonaniu krzyżowania dzieci zastępują w populacji rodziców. Oczywiście w tym kroku nie wszystkie rozwiązania muszą się ze sobą krzyżować. Liczbę krzyżowań określa tzw. współczynnik krzyżowania (o wartości od 0 do 1), który pokazuje jaka liczba osobników powinna być w jednej iteracji skrzyżowana, bądź określa prawdopodobieństwo z jakim każde rozwiązanie może wziąść udział w krzyżowaniu.
W przypadku binarnej reprezentacji chromosomu najprostrze krzyżowanie polega na podziale dwóch chromosomów (rodzice) na dwie części (niekoniecznie równe) i z nich tworzone są dzieci: pierwsze dziecko składa się z początkowej części pierwszego rodzica i końcówki drugiego natomiast drugie dziecko odwrotnie - początek drugiego rodzica i koniec pierwszego.
Na przykładzie homo sapiensa może to wyglądać następująco:
Pierwszy rodzic: 00000000 - niebieskooka Polka o wzroście do 140cm
Drugi rodzic: 11011001 - wysoki (190-200) Niemiec o brązowych oczach.
Jeśli punkt podziału ustalimy pomiędzy czwartym a piątym bitem to dzieci będą wyglądać następująco:
00001001 - Niemka o niebieskich oczach i wzroście 150-160cm
11010000 - Polak o brązowych oczach i wzorście 160-170cm
Rozszerzeniem tego krzyżowania jest krzyżowanie wielopunktowe, gdzie chromosomy rodziców dzieli się na kilka części a później dzieci tworzy się na podstawie przeplatanych wycinków rodziców.
W przypadku niebinarnej reprezentacji gatunku należy wymyśleć krzyżowanie stosowne do zastosowanej reprezentacji. Gdy np. dane trzymane są w strukturze to możne podmieniać pomiędzy rodzicami zawartości poszczególnych pól struktur. W tym wypadku jednak dzieci będą zawsze zawierały wartości występujące przynajmniej u jednego z rodziców. W powyższym przykładzie krzyżowania jednopunktowego wzrost dzieci jest różny od wzrostu rodziców. Stało się tak dlatego, że punkt podziału trafił w środku bitów odpoweidzialnych za wzrost. W przypadku kodowania niebinarnego takie coś byłoby niemożliwe.
Mutacja
Mutacja podobnie jak krzyżowanie zapewnia dodawanie do populacji nowych osobników. Jednak w odróżnieniu od krzyżowania w przypadku mutacji modyfikowany jest jeden a nie dwa osobniki. Podobnie jak w przypadku krzyżowania istnieje tzw. współczynnik mutacji, który określa ile osobników będzie w jednej iteracji ulegało mutacji.
W przypadku reprezentacji binarnej sprawa mutacji jest bardzo prosta wystarczy np. zanegować jeden bit w rozwiązaniu aby otrzymać zupełnie nowego osobnika. W przypadku homo sapiensa negacja pierwszeo bitu powoduje zamianę kobiety na mężczyznę lub odwrotnie. Oczywiście mutacja może być bardziej urozmaicona (negacja losowej liczby bitów, odwracanie kolejności losowej liczby bitów, przesunięcie losowej liczby bitów i inne.), należy jednak pamiętać, że operować ona może tylko na jednym rozwiązaniu.
W przypadku niebinarnej reprezentacji rozwiązania mutacja może polegać np. na wpisaniu do losowego pola struktury losowej wartości (oczywiście przewidzianej przez gatunek).
Powrót do oceny osobników
W zasadzie algorytm genetyczny powinien działać w nieskończoność jednak dobrze jest zapewnić jakieś rozsądne wyjście z pętli. Może to być np. pewna liczba iteracji, wartość osiągniętego najlepszego rozwiązania, czas, brak poprawy wyniu przez pewną ilość iteracji lub inne w zależnośći od rodzaju zadania.
Powyżej zostały opisane podstawowe elementy algorytmu genetycznego, które w zupełności wystarczają do napisania programu rozwiązującego taki czy inny problem. Oczywiście istnieją jeszcze pewne techniki usprawniające algorytm, ale o nich może innym razem.
Komiwojażer musi odwiedzić wszystkie miasta z zadanego regionu i wrócić do miasta początkowego (jest to problem szukania cyklu). Wszystkie miasta są ze sobą połączone (mamy do czynienia z grafem pełnym, czyli kliką). Mając do dyspozycji macierz odlebłości pomiędzy poszczególnymi miastami należy znaleść cykl o najmniejszym koszcie. I jeszcze jedno: każde miasto nie może być odwiedzone więcej niż jeden raz.
A więc na wejściu mamy informację o odległościach pomiędzy miastami, a na wyjściu należy wygenerować najlepszą kolejność odwiedzanych miast.
Nie zawsze jednak dysponujemy od razu macierzą odległości. Czasami dane o miastach zapisane są w postaci listy miast wraz z ich współrzędnymi. W tym wypadku do stworzenia macierzy odległości należy wykorzystać wzór na odległość Euklidesową pomiędzy dwoma punktami. Na płaszczyźnie będzie to coś takiego:
Odl(a,b)=sqrt((xa-xb)*(xa-xb)+(ya-yb)*(ya-yb)) , czyli po prostu pierwiastek z sumy kwadratów różnic odległości dla poszczególnych współrzędnych.
Dla przykladu:
...oraz obliczona na podstawie listy współrzędnych macierz odległości (troche niedokładnie, bo pominięte zostały wartści liczb po przecinku...):
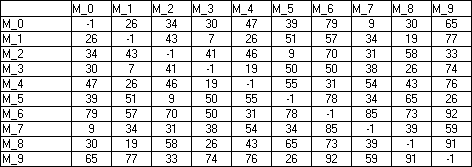
Możliwych tras dla n miast jest coś koło n! (dodanie i-tego miasta powoduje zwiekszenie liczby możliwych tras i-krotnie). Sprawdzenie ich wszystkich jest zadaniem bardzo czasochłonnym... Dlatego do znalezienia najlepszej wykorzystane zostaną algorytmy genetyczne.
Populacja początkowa będzie składała się z pewnej liczby tras wygenerowanych zupełnie losowo. Należy w tym miejscu przez chwilę zastanowić się nad reprezentacją pojedynczego rozwiązania. Ze względu na fakt, że rozwiązaniem problemu komiwojażera jest lista kolejno odwiedzanych miast, natychmiastowym pomysłem na reprezetntację rozwiązania jest właśnie lista kolejnych miast. Jest to reprezentacja bardzo prosta i bardzo szybka jeśli chodzi o wyliczenie funkcji oceny dla każdego osobnika. Ma ona jednak bardzo dużą wadę. Mianowicie skrzyżowanie dwóch tras może dać osobnika nieprawidłowego.
Np. skrzyżowanie trasy 1-2-3-4-5 z trasą 4-5-1-3-2 w punkcie między drugim, a trzeciem miastem da następujących potomków: 1-2-1-3-2 oraz 4-5-3-4-5. Żadne z dzieci nie jest poprawne (zawierają kilkukrotne wystąpienie tych samych miast, a jednocześnie pewne miasta wogóle nie występują). Dlatego w przypadku takiej reprezentacji należy zadbać albo o naprawę pokrzyżowanych osobników, albo o zmianę standardowego operatora krzyżowania jakimś bardziej wymyślnym. Ale o tym za chwilę przy opisie operatorów genetycznych.
Innym sposobem reprezentacji trasy jest lista pokazująca kolejność pobierania miast do tworzonej trasy. Wyjaśnienie mało jasne, więc od razu mały przykładzik:
Punktem odniesienia dla tej reprezentacji jest lista kolejnych miast: 1-2-3-4-5. Pojedynczy osobnik np. 4-4-1-2-1 pokazuje w jakiej kolejności wybierane są kolejno odwiedzane miasta. Na początku jest czwórka więc pierwszym odwiedzanym miastem będzie miasto umieszczone na czwartej pozycji w liście odniesienia, czyli czwórka. Czwórkę tą usuwa się z listy odniesienia (pozostają miasta 1-2-3-5), natomiast lista odwiedzanych miast wygląda następująco: 4
Kolejnym elementem osobnika jest ponownie czwórka. W tej chwili na czwartym miejscu listy odniesienia jest piątka, więc kolejnym odwiedzanym miastem będzie miasto nr 5, a lista odniesienia będzie wyglądała następująco: 1-2-3. W kolejnych krokach będzie to wyglądało następująco:
Reprezentacja ta wprowadza spore zamieszanie przy przechodzeniu na reprezentację wykorzystywaną przy funcji oceny, jednak kłopoty te rekompensuje przy krzyżowaniu i mutacji. Cechą charakterystyczą tej reprezentacji jest fakt, że na i-tej pozycji jest liczba z przedziału od 1 do n-i+1 (gzie n to liczba wszystkich miast). Ze względu na to wymiana materiału genetycznego między dwoma osobnikami za pomocą standardowego krzyżowania x-punktowego zawsze da dopuszczalne potomstwo.
Kolejnym elementem algorytmu gentycznego jest ocena osobników. Oczywiście w przypadku problemu komiwojażera oceną poszczególnych osobników jest długość trasy jaką reprezentują.
Dla przykładu:
Zajmijmy się teraz sprawą krzyżowania. Wcześniej napisałem, że w przypadku reprezentacji 'naturalnej' standardowe krzyżowanie x-punktowe specjalnie dobrze się nie sprawuje. Dlatego dla problemu komiwojażera (i innych jemu podobnych) wymyślono kilka innych rodzajów krzyżowań, które zawsze dają rozwiązania dopuszczalne. Poniżej przedstawię dwa z nich:
Jeśli chodzi o mutację to sytuacja jest bardzo podobna: w zależności od rodzaju reprezentacji można zastosować standardowe operatory mutacji, bądź jakieś bardziej wyrafinowane. W przypadku reprezentacji 'naturalnej' najprostrzym rodzajem mutacji jest wymiana ze sobą dwóch miast w rozwiązaniu. Np:
1-2-3-4-5 -> wymiana miast 2 i 4 -> 1-4-3-2-5
Można również zmieniać kolejność przechodzenia miast. Np:
1-2-3-4-5 -> Zmiana kolejności w obrębie miast 1 i 4 -> 4-3-2-1-5
Można również przesunąć jakieś miasto (lub grupę miast) w ramach rozwiązania. Np:
1-2-3-4-5 -> Wstawienie miasta 1 pomiędzy 4 i 5 -> 2-3-4-1-5
Dla drugiej reprezentacji taka zabawa jest niepotrzebna ponieważ w tym przypadku mutacja sprowadza się do zamiany wartości z pozycji i losową wartością z przedziału od 1 do n-i+1 (n - liczba wszystkich miast).
I tak mniej więcej wyglądają poszczególne elementy algorytmu genetycznego rozwiązującego problem komiwojażera. Oczywiście ten tekst nie wyczerpuje w całości tego zagadnienia (istnieją jeszcze inne sposoby reprezentacji rozwiązania, istnieją inne rodzaje mutacji, krzyżowania), ale mam nadzieję, że ludziom którzy chcą po prostu gdzieś wykorzystać algorytmy genetyczne przyda się, jako krótkie przedstawienie praktyczego wykorzystania. Więcej na temat rozwiązywania problemu komiwojażera można znaleźć w [I].
Populacja - reprezentacja pojedynczego rozwiązania
W przypadku programowania genetycznego najczęściej stosowaną reprezentacją pojednynczego rozwiązania jest struktura drzewiasta. Jest ona bardzo wygodna z punktu widzenia krzyżowania i mutacji, a poza tym wymusza kolejność przechodzenia przez węzły i liście. Jest to reprezentacja o zmiennej długości ponieważ przykładowymi programami mogą być zarówno program wykonujący sumę dwóch argumentów jak i program obliczający pierwiastki równania kwadratowego.
Przykładowy program może wyglądać następująco:
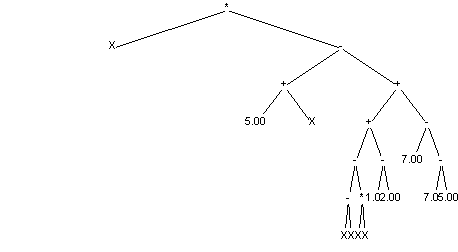
Wynikiem działania każdego programu jest pewna wartość. Aby ją wyznaczyć należy drzewo przeglądać wstecznie (przed wykonaniem działania zapisanego w węźle należy najpierw obliczyć wyrażenia 'zaczepione' w jego dzieciach). Wartość zwracana przez powyższe drzewo jest określona wzorem:
(X*((5.00+X)-((((X-X)-(X*X))+(1.00-2.00))+(7.00-(7.00-5.00)))))
Elementami takiego drzewa mogą być:
- Jako węzły:
* Operatory arytmetyczne (+,-,/,...)
* Operatory logiczne (&&,||,!,...)
* Operatory bitowe (&,|,~,...)
* Porównania (>,<,==,...)
* Funkcje (trygonometryczne, potęgowe,...)
* Instrukcja warunkowa - IF (jeśli spełniony jest warunek (pierwszy argument), wykonywane jest poddrzewo drugiego argumentu, jeśli nie trzeciego)
* Instrukcja iteracyjna - FOR (pierwszy argument podaje ile razy ma zostać wykonane poddrzewo drugiego argumentu)
- Jako liście
* Wartości stałe, zmienno- lub stałoprzecinkowe (np.: 5, 10.5, -11)
* Wartości zmiennych (np.: X)
* Wywołania funkcji (np.: WczytajZnakZKlawiatury(), lub random())
* Wywołania procedur (np.: printf(), clrscr()) - W przypadku procedur problemem jest zwracana przez nie wartość (każdy element drzewa musi coś zwracać swojemu rodzicowi) - najczęściej przyjmuje się, że procedury zwracają zero.
Populacja początkowa wypełniona jest programami wygenerowanym całkowicie losowo. Podczas losowania osobników dobrze jest zadbać o to, aby osobniki nie były zbyt 'rozrośnięte'. Można to zrobić ustalając maksymalną głębokość lub liczbę wierzchołków tworzonego drzewa.
Krzyżowanie
Krzyżowanie polega na wymianie pomiędzy dwoma osobnikami wybranych losowo poddrzew. Poniżej przedstawiony jest przykład krzyżowania (ramką zaznaczone zostały wymieniane poddrzewa):
Sytuacja przed krzyżowaniem:
Pierwszy rodzic:
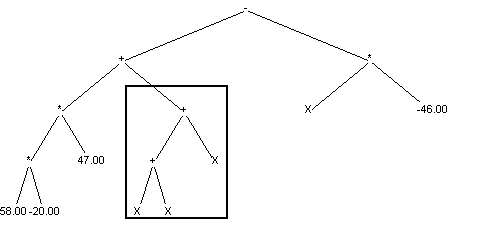
Drugi rodzic:
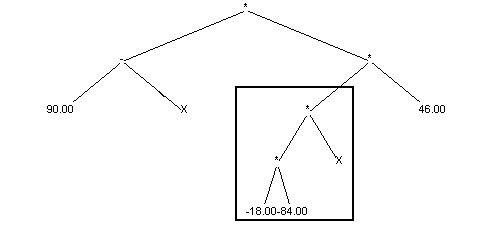
Sytuacja po krzyżowaniu:
Pierwsze dziecko:
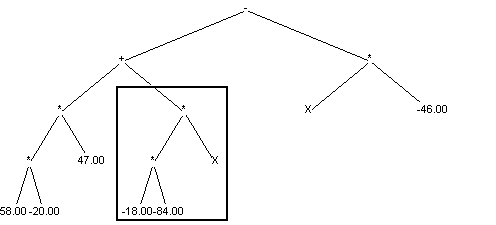
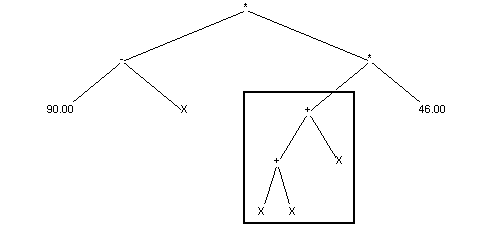
Drugie dziecko:
Mutacja
Najczęściej stosowaną mutacją w przypadku programowania genetycznego jest usunięcie z osobnika losowego poddrzewa i na jego miejsce wygenerowanie nowego. Poniżej znajduje się przykład takiej mutacji (ramką zastało zaznaczone poddrzewo usuwane oraz dodawane):
Osobnik przed mutacją:
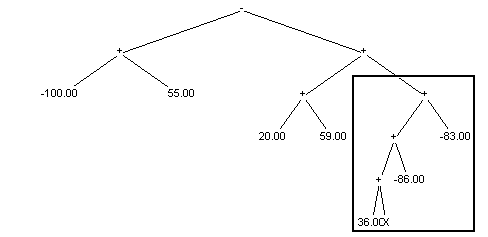
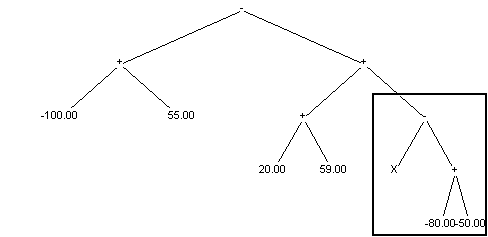
Osobnik po mutacji:
Innym sposobem mutacji jest zmiana operatowa w dowolnym wierzchołku drzewa. Należy tutaj pamiętać, że jeśli nowy operator ma mniej argumentów niż oryginalny (max(a,b)->sin(a)) należy usunąć nadmiarowe poddrzewa. Jeśli natomiast nowy operator ma więcej argumentów (max(a,b)->if(a,b,c)) należy dogenerować brakujące poddrzewa.
Można również mutować liście w drzewie. Jest to najprostrzy rodzaj mutacji (nie trzeba dodawać nowych, ani usuwać starych poddrzew), jednak powoduje niewielką zmianę działania programu jaki mutowany osobnik reprezentuje. Ten sposób mutacji przydaje się gdy rozwiązanie (osobnik, program) działa 'z grubsza' poprawnie a trzeba zmienić tylko jakieś współczynniki (np. zmiana liczby iteracji, próg do porównania dla instrukcji IF, itp.)
Funkcja oceny
Głównym zadaniem funkcji oceny jest sprawdzenie czy dany osobnik wykonuje taki program o jaki nam chodziło. W zależności od tego jak bardzo wyniki programu przypominają to o co nam chodziło osobnik dostaje odpowiednią liczbę punktów. Np dla rozwiązywania zadania aproksymacji funkcji funkcja oceny sprawdza jak daleko wygenerowana funkcja odbiega od punktów bazowych.
Do funkcji oceny warto jest dodać pewną karę za wielkość osobnika. Dzięki temu poszczególne osobniki nie będą się nadmiernie rozrastać. W przypadku drzewowej reprezentacji rozwiązania można wprowadzić karę za liczbę wierzchołków oraz karę za maksymalną głębokość drzewa.
Selekcja
Ta część algorytmu jest dokładnie taka sama jak w przypadku innych wykorzystań algorytmów genetycznych. Zarówno koło ruletki jak i metoda turniejowa bazują tylko na wartościach funkcji oceny (do działania nie potrzebują informacji o osobnikach).
Iteracyjne wykonywanie wszystkich kroków AG prowadzi do otrzymania programu (przynajmniej w przybliżeniu) rozwiązującego zadany problem. Niestety (na szczęście?) program wygenerowany dzięki programowaniu genetycznemu jest daleki od optymalnego (dlatego, póki co, programiści nie stracą pracy). Zaletą progamowania genetycznego jest fakt, że tworzenie programu w ten sposób nie wymaga żadnych nakładów pracy ze strony programisty.
Tutaj mamy program "Genetyk" za pomocą którego możemy sprawdzić na własne oczy działanie programowania genetycznego. Program ten próbuje znaleźć wzór funcji przechodzącej przez zadane punkty (aproksymacja).
Kolor oczu (mamy do wyboru: niebieskie, piwne, brązowe i czarne)
Wzrost (poniżej 140, 140-150, 150-160, 160-170, 170-180, 180-190, 190-200, powyżej 200)
Narodowość (mamy do wyboru: Polak, Niemiec, Czech, Rosjanin)
Najprosztrzą reprezentacją homo sapiensa wydaje się być struktura w której będą zapamiętywane wartości poszczególnych atrybutów. Jeśli na każdy atrybut przeznaczymy zmienną typu char* (string) to otrzymamy całkiem pokaźny rozmiar osobnika. Dodatkową wadą takiej reprezentacji jest dostyć duża niewygoda krzyżowania i mutacji (o której będzie mowa za chwilę). Niewątpliwą zaletą tej reprezentacji jest jest 'bezpośredniość', wszystkie pola struktury pamiętają konkretną wartość atrybutu. Celem zmniejszenia rozmiaru struktury można przyjąć, że dla przechowywania wartości atrybutów wykorzystane zostaną zmienne liczbowe (int, byte...) wtedy rozmiar naszej struktury opisującej człowieka zmniejszy się do 4 bajtów. W tym wypadku nie będziemy mieli w strukturze natychmiastowej informacji o wartościach atrybutów i w związku z tym należy stosować pewne oznaczenia. Np: dla płci 0 oznacza kobietę, 1 oznacza mężczyznę, dla koloru oczu 0 oznacza niebieskie, 1 oznacza piwne, 2 oznacza brązowe, 3 oznacza czarne. Reprezentacja ta jest już niewielka i całkiem wygodna w późniejszej obsłudze. Można się jednak w opisie homo sapiensa posunąć trochę dalej i wykorzystać reprezentację bitową. Proszę zauważyć, że do reprezentacji płci wystarczy jeden bit (wartość zero-kobieta, jeden-mężczyzna), do reprezentacji koloru oczu dwa bity (00-niebieskie, 01-piwne, 10-zielone, 11-czarne), do reprezentacji wzrostu też trzy bity, a do reprezentacji narodowości dwa bity. I w przypadku takiego kodowania wartości wszystkich atrybutów mieszczą się w 8 bitach. Te 8 bitów tworzą całkowity obraz pojedynczego osobnika. Przy tej reprezentacji należy na początku przyjąć w jakiej kolejności poszególne atrybuty będą występowały w reprezentacji osobnika. W naszym przypadku przyjmijmy, że pierwszy bit będzie informował o płci następne o kolorze oczu, wzroście i narodowości. Dla przykładu chromosom: 00000000 reprezentuje niebieskooką Polkę o wzroście nieprzekraczającym 140cm, a chromosom 11011001 reprezentuje wysokiego (190-200) Niemca o brązowych oczach.
I jeszcze jeden przykładzik pokazujący jak można stworzyć binarną reprezentację liczb naturalnych. Przyjmijmy, że mamy do rozwiązania problem znalezienia takiego x'a dla którego funkcja postaci y=f(x) ma minimum (maksimum). Szukamy po prostu ekstremów funkcji. W tym przypadku pojednycze rozwiązanie ma reprezentować pojedynczą wartości x'a. Można do tego celu użyć zmiennej typu float (real), jednak wtedy trudno jest wymyśleć jakiś rozsądny sposób krzyżowania takich osobników. Innym wygodniejszym sposobem kodowania x'ów jest zastosowanie reprezentacji bitowej. W tym wypadku tracimy jednak na maksymalnej rozdzielczości. Dla przykładu jeśli badamy funkcję w przedziale 1-3 i reprezentujemy x'y na 4 bitach to otrzymujemy maksymalną rozdzielczość:
(max_x-min_x)/(2^(liczba_bitów)-1)=(3-1)/(2^4-1)=2/15=0.1333
Oznacza to, że najmniejsza możliwa różnica pomiędzy analizowanymi x'ami jest równa 0,13333. Następujące wartości bitów odpowiadają następującym wartościami x'a:
0000-1.0
0001-1.1333
0010-1.2666
0011-1.4 itd.
Jeśli mamy już zaprojektowany chromosom (krótki i wygodny w obsłudze) możemy zająć się samym algorytmem. W uproszczeniu wygląda on następująco:
1. Losowanie populacji
2. Ocena osobników
3. Selekcja
4. Krzyżowanie
5. Mutacja
6. Powrót do punktu 2
Poniżej opis poszczególnych jego elementów:
Losowanie populacji
W tym miejscu należy ustalić jak wielka będzie tworzona populacja. Jeśli populacja będzie zawierała zbyt mało osobników to algorytm może zatrzymać się w jakimś minimum lokalnym (gdy jakieś niezłe (ale nie najlepsze) rozwiązanie zdominuje całą populację). Z drugiej strony zbyt duża liczebność populacji zmniejsza szybkość działania algorytmu. Po ustaleniu wielkości populacji należy stworzyć wszystkie osobniki. Ze względu na fakt, że początkowa populacja powinna być jak najbardziej różnorodna każdy osobnik powinien być tworzony całkowicie losowo. W tym miejscu widać przewagę reprezentacji bitowej gdzie bez względu na rodzaj problemu nowo tworzony osobnik zawiera n losowo wygenerowanych bitów. W przypadku reprezentacji osobnika w strukturze należy każde jej pole wypełnić osobno. Na tym kroku należy pamiętać aby tworzone osobniki były poprawne to znaczy reprezentowały obiekty należące do dziedziny problemu. Np przy tworzeniu x'ów (problem znajdowania ekstremum) w przedziale 1-3 wygenerowany chromosom nie może reprezentować x'a o wartości np. 5. W przypadku reprezentacji bitowej ten problem pojawia się wtedy gdy do reprezentowania jakiegoś atrybutu nie są wykożystywane wszystkie kombinacje bitów. Wracając do poprzedniego przykładu chromosomu opisującego homo sapiensa, jeśli nie uwzględnialibyśmy Rosjan to chromosom 000000011 nie byłby poprawny.
Ocena osobników
W tym kroku banana jest 'dobroć' poszczególnych osobników. W zależności od rodzaju problemu różne są funkcje sprawdzające przystosowanie osobników. W przypadku ekstremum funkcji 'dobrocią' jest po prostu wartość funkcji w zadanym x'ie. W przypadku rozwiązywania problemu komiwojażera jest to długość trasy jaka jest reprezentowana przez danego osobnika. W tym miejsu można wprowadzić tzw. funkcję kary za niedopuszczalne rozwiązanie. Wcześniej wspomniałem, że o poprawne osobniki należy zadbać podczas tworzenia populacji (niepoprawne osobniki mogą też powstawać w krokach krzyżowania i mutacji). Czasmami jest to jednak trudne do wykonania dlatego przy losowaniu można te osobniki zaakceptować a w tym kroku dodać funkcję kary. Spowoduje ona dużo mniejsze prawdopodobieństwo przejścia przez danego osobnika kroku selekcji. W zależności od tego czy funkcję dopasowania ('dobroć') minimalizujemy czy maksymalizujemy wartość funkcji błędu należy do niej dodać bądź odjąć.
Selekcja
Krok ten jest esensją całej genetyki. W tym miejscu tworzona jest nowa populacja na podstawie już istniejącej. W zależności od wartości funkcji oceny (obliczanej w poprzednim kroku) dany osobnik ma większe (gdy jest 'dobry') lub mniejsze (gdy jest 'słaby') szanse na znalezienie się w kolejnym pokoleniu. Istnieje kilka sposobów obliczania 'szansy' poszczególnych osobników:
Koło ruletki - Polega na n krotnym losowaniu (n - liczba osobników w populacji) ze starej populacji osobników, które zostaną przepisane do nowej populacji. Oczywiście wszystkie osobniki mają różne prawdopodobieństwa wylosowania. Prawdopodobieństwo to jest liczone z następującego wzoru:
Wartość przystosowania danego osobnika/suma wartości przystosowania wszystkich osobników
Powyższy wzór jest poprawny tylko wtedy gdy maksymalizujemy funkcję oceny. Gdybyśmy ją minimalizowali można zastosować następujący wzór:
(Wartość najgorszego osobnika-Wartość danego osobnika+1)/(suma wartości wszystkich osobników+1)
Wzór ten odwraca minimalizację na maksymalizację.
I od razu mały przykład (przyjmijmy maksymalizację funkcji przystosowania). Mamy trzy osobniki o następujących wartościach przystosowania: 5,1,2. Odpowiadające im wartości prawdopodobieństwa są zatem równe:
* Pierwszy osobnik: 5/8, czyli 62,5%
* Drugi osobnik: 1/8, czyli 12,5%
* Trzeci osobnik: 2/8, czyli 25%
Ranking liniowy - Selekcja tą metodą jest bardzo podobna do selekcji metodą koła ruletki. Modyfikacja polega jedynie na zmianie funkcji określającej prawdopodobieństwo wyboru danego osobnika. Przed przystąpieniem do tej selekcji należy nadać każdemu z osobników pewną wartość (przystosowanie) zależną od jego położenia na liście posortowanej względem wartości funkcji oceny. Jeśli chcemy maksymalizować to wartości powinny być posortowane rosnąco, w przypadku minimalizacji wartości powinny być posortowane malejąco. Aby obliczyć prawdopodobieństwo wybrania każdego osobnika można skorzystać ze wzoru:
Prawdopodobieństwo=Przystosowanie/Suma przystosowania wszystkich osobników
Dla powyższego przykładu wartości prawdopodobieństw wyglądałyby następująco:
* Pierwszy osobnik: 3/6, czyli 50%
* Drugi osobnik: 1/6, czyli 16,7%
* Trzeci osobnik: 2/6, czyli 33,3%
Ten sposób wyliczania prawdopodobieństw zmniejsza przewagę jaką mają najlepsze rozwiązania, gdy ich przewaga jest b.duża i zwiększa przewagę gdy jest ona b.mała.
Turniej - Metoda jest zupełnie różna od powyższych i polega na losowym wyborze z całej populacji kilku osobników (jest to tzw. grupa turniejowa), a później z tej grupy wybierany jest osobnik najlepiej przystosowany i on przepisywany jest do nowo tworzonej populacji. Losowanie grup turniejowych oraz wybieranie z nich najlepszego osobnika należy powtórzyć aż do utworzenia całej nowej populacji.
Selekcja metodą turniejową jest pozbawiona niedogodności metody koła ruletki, gdzie wymagana jest maksymalizacja funkcji oceny, w turnieju ważna jest jedynie informacja o 'lepszości' jednego rozwiązania nad innym.
Krzyżowanie
Zadaniem kroku krzyżowania jest wymiana "materiału genetycznego" pomiędzy dwoma rozwiązaniami w populacji. W wyniku krzyżowania na podstawie dwóch rozwiązań (rodzice) tworzone są dwa nowe osobniki (dzieci). Po wykonaniu krzyżowania dzieci zastępują w populacji rodziców. Oczywiście w tym kroku nie wszystkie rozwiązania muszą się ze sobą krzyżować. Liczbę krzyżowań określa tzw. współczynnik krzyżowania (o wartości od 0 do 1), który pokazuje jaka liczba osobników powinna być w jednej iteracji skrzyżowana, bądź określa prawdopodobieństwo z jakim każde rozwiązanie może wziąść udział w krzyżowaniu.
W przypadku binarnej reprezentacji chromosomu najprostrze krzyżowanie polega na podziale dwóch chromosomów (rodzice) na dwie części (niekoniecznie równe) i z nich tworzone są dzieci: pierwsze dziecko składa się z początkowej części pierwszego rodzica i końcówki drugiego natomiast drugie dziecko odwrotnie - początek drugiego rodzica i koniec pierwszego.
Na przykładzie homo sapiensa może to wyglądać następująco:
Pierwszy rodzic: 00000000 - niebieskooka Polka o wzroście do 140cm
Drugi rodzic: 11011001 - wysoki (190-200) Niemiec o brązowych oczach.
Jeśli punkt podziału ustalimy pomiędzy czwartym a piątym bitem to dzieci będą wyglądać następująco:
00001001 - Niemka o niebieskich oczach i wzroście 150-160cm
11010000 - Polak o brązowych oczach i wzorście 160-170cm
Rozszerzeniem tego krzyżowania jest krzyżowanie wielopunktowe, gdzie chromosomy rodziców dzieli się na kilka części a później dzieci tworzy się na podstawie przeplatanych wycinków rodziców.
W przypadku niebinarnej reprezentacji gatunku należy wymyśleć krzyżowanie stosowne do zastosowanej reprezentacji. Gdy np. dane trzymane są w strukturze to możne podmieniać pomiędzy rodzicami zawartości poszczególnych pól struktur. W tym wypadku jednak dzieci będą zawsze zawierały wartości występujące przynajmniej u jednego z rodziców. W powyższym przykładzie krzyżowania jednopunktowego wzrost dzieci jest różny od wzrostu rodziców. Stało się tak dlatego, że punkt podziału trafił w środku bitów odpoweidzialnych za wzrost. W przypadku kodowania niebinarnego takie coś byłoby niemożliwe.
Mutacja
Mutacja podobnie jak krzyżowanie zapewnia dodawanie do populacji nowych osobników. Jednak w odróżnieniu od krzyżowania w przypadku mutacji modyfikowany jest jeden a nie dwa osobniki. Podobnie jak w przypadku krzyżowania istnieje tzw. współczynnik mutacji, który określa ile osobników będzie w jednej iteracji ulegało mutacji.
W przypadku reprezentacji binarnej sprawa mutacji jest bardzo prosta wystarczy np. zanegować jeden bit w rozwiązaniu aby otrzymać zupełnie nowego osobnika. W przypadku homo sapiensa negacja pierwszeo bitu powoduje zamianę kobiety na mężczyznę lub odwrotnie. Oczywiście mutacja może być bardziej urozmaicona (negacja losowej liczby bitów, odwracanie kolejności losowej liczby bitów, przesunięcie losowej liczby bitów i inne.), należy jednak pamiętać, że operować ona może tylko na jednym rozwiązaniu.
W przypadku niebinarnej reprezentacji rozwiązania mutacja może polegać np. na wpisaniu do losowego pola struktury losowej wartości (oczywiście przewidzianej przez gatunek).
Powrót do oceny osobników
W zasadzie algorytm genetyczny powinien działać w nieskończoność jednak dobrze jest zapewnić jakieś rozsądne wyjście z pętli. Może to być np. pewna liczba iteracji, wartość osiągniętego najlepszego rozwiązania, czas, brak poprawy wyniu przez pewną ilość iteracji lub inne w zależnośći od rodzaju zadania.
Powyżej zostały opisane podstawowe elementy algorytmu genetycznego, które w zupełności wystarczają do napisania programu rozwiązującego taki czy inny problem. Oczywiście istnieją jeszcze pewne techniki usprawniające algorytm, ale o nich może innym razem.
Co zorbić żeby się komiwojażer nie przepracował...
Ten tekst będzie opowiadał o starym jak świat problemie NP-trudnym znanym pod nazwą: 'problem komiwojażera'. Na początku może kilka słów na czym ten problem polega:Komiwojażer musi odwiedzić wszystkie miasta z zadanego regionu i wrócić do miasta początkowego (jest to problem szukania cyklu). Wszystkie miasta są ze sobą połączone (mamy do czynienia z grafem pełnym, czyli kliką). Mając do dyspozycji macierz odlebłości pomiędzy poszczególnymi miastami należy znaleść cykl o najmniejszym koszcie. I jeszcze jedno: każde miasto nie może być odwiedzone więcej niż jeden raz.
A więc na wejściu mamy informację o odległościach pomiędzy miastami, a na wyjściu należy wygenerować najlepszą kolejność odwiedzanych miast.
Nie zawsze jednak dysponujemy od razu macierzą odległości. Czasami dane o miastach zapisane są w postaci listy miast wraz z ich współrzędnymi. W tym wypadku do stworzenia macierzy odległości należy wykorzystać wzór na odległość Euklidesową pomiędzy dwoma punktami. Na płaszczyźnie będzie to coś takiego:
Odl(a,b)=sqrt((xa-xb)*(xa-xb)+(ya-yb)*(ya-yb)) , czyli po prostu pierwiastek z sumy kwadratów różnic odległości dla poszczególnych współrzędnych.
Dla przykladu:
Lista miast i ich współrzędnych: | ...oraz odpowiadająca im mapa: |

Możliwych tras dla n miast jest coś koło n! (dodanie i-tego miasta powoduje zwiekszenie liczby możliwych tras i-krotnie). Sprawdzenie ich wszystkich jest zadaniem bardzo czasochłonnym... Dlatego do znalezienia najlepszej wykorzystane zostaną algorytmy genetyczne.
Populacja początkowa będzie składała się z pewnej liczby tras wygenerowanych zupełnie losowo. Należy w tym miejscu przez chwilę zastanowić się nad reprezentacją pojedynczego rozwiązania. Ze względu na fakt, że rozwiązaniem problemu komiwojażera jest lista kolejno odwiedzanych miast, natychmiastowym pomysłem na reprezetntację rozwiązania jest właśnie lista kolejnych miast. Jest to reprezentacja bardzo prosta i bardzo szybka jeśli chodzi o wyliczenie funkcji oceny dla każdego osobnika. Ma ona jednak bardzo dużą wadę. Mianowicie skrzyżowanie dwóch tras może dać osobnika nieprawidłowego.
Np. skrzyżowanie trasy 1-2-3-4-5 z trasą 4-5-1-3-2 w punkcie między drugim, a trzeciem miastem da następujących potomków: 1-2-1-3-2 oraz 4-5-3-4-5. Żadne z dzieci nie jest poprawne (zawierają kilkukrotne wystąpienie tych samych miast, a jednocześnie pewne miasta wogóle nie występują). Dlatego w przypadku takiej reprezentacji należy zadbać albo o naprawę pokrzyżowanych osobników, albo o zmianę standardowego operatora krzyżowania jakimś bardziej wymyślnym. Ale o tym za chwilę przy opisie operatorów genetycznych.
Innym sposobem reprezentacji trasy jest lista pokazująca kolejność pobierania miast do tworzonej trasy. Wyjaśnienie mało jasne, więc od razu mały przykładzik:
Punktem odniesienia dla tej reprezentacji jest lista kolejnych miast: 1-2-3-4-5. Pojedynczy osobnik np. 4-4-1-2-1 pokazuje w jakiej kolejności wybierane są kolejno odwiedzane miasta. Na początku jest czwórka więc pierwszym odwiedzanym miastem będzie miasto umieszczone na czwartej pozycji w liście odniesienia, czyli czwórka. Czwórkę tą usuwa się z listy odniesienia (pozostają miasta 1-2-3-5), natomiast lista odwiedzanych miast wygląda następująco: 4
Kolejnym elementem osobnika jest ponownie czwórka. W tej chwili na czwartym miejscu listy odniesienia jest piątka, więc kolejnym odwiedzanym miastem będzie miasto nr 5, a lista odniesienia będzie wyglądała następująco: 1-2-3. W kolejnych krokach będzie to wyglądało następująco:
| Analizowany element osobnika | Lista odniesienia | Tworzona lista odwiedzanych miast |
| 1 | 1-2-3 | 4-5-1 |
| 2 | 2-3 | 4-5-1-3 |
| 1 | 2 | 4-5-1-3-2 |
Reprezentacja ta wprowadza spore zamieszanie przy przechodzeniu na reprezentację wykorzystywaną przy funcji oceny, jednak kłopoty te rekompensuje przy krzyżowaniu i mutacji. Cechą charakterystyczą tej reprezentacji jest fakt, że na i-tej pozycji jest liczba z przedziału od 1 do n-i+1 (gzie n to liczba wszystkich miast). Ze względu na to wymiana materiału genetycznego między dwoma osobnikami za pomocą standardowego krzyżowania x-punktowego zawsze da dopuszczalne potomstwo.
Kolejnym elementem algorytmu gentycznego jest ocena osobników. Oczywiście w przypadku problemu komiwojażera oceną poszczególnych osobników jest długość trasy jaką reprezentują.
Dla przykładu:
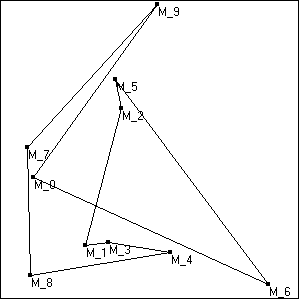 | 0-6-5-2-1-3-4-8-7-9 Wartość funkcji oceny: 0-6 -> 79 6-5 -> 78 5-2 -> 9 2-1 -> 43 1-3 -> 7 3-4 -> 19 4-8 -> 43 8-7 -> 39 7-9 -> 59 9-0 -> 65 Suma: 441 |
Zajmijmy się teraz sprawą krzyżowania. Wcześniej napisałem, że w przypadku reprezentacji 'naturalnej' standardowe krzyżowanie x-punktowe specjalnie dobrze się nie sprawuje. Dlatego dla problemu komiwojażera (i innych jemu podobnych) wymyślono kilka innych rodzajów krzyżowań, które zawsze dają rozwiązania dopuszczalne. Poniżej przedstawię dwa z nich:
- Krzyżowanie z częściowym odwzorowaniem (PMX)
Przy tym krzyżowaniu wybiera się losowo pewną podtrasę w obu rodzicach i przekazuje się ją do potomka (podtrasa pierwszego rodzica trafia do drugiego potomka i na odwrót):
Rodzic pierwszy: 1-2-3-4-5, rodzic drugi: 2-4-3-5-1, pozostawiana podtrasa: miasta od 2 do 4:
Pierwsze dziecko: x-4-3-5-x, drugie dziecko x-2-3-4-x
Teraz uzupełnia się te trasy tak żeby nie powstał konflikt (dwa takie same miasta w trasie): Pierwsze dziecko: 1-4-3-5-x, drugie dziecko x-2-3-4-1 (do dzieci nie można dodać miasta 5 (do pierwszeo) ani 2 (do drugiego) ponieważ pojawiłyby się dwa takie same miasta w trasie)
Następnie tworzone są odwzorowania (na podstawie wymienianych podtras): 2<->4, 3<->3, 4<->5 i za ich pomocą uzupełniane są dzieci:
W pierwszym brakuje piątki więc na to miejsce wstawiamy miasto nr 2 (5<->4 i 4<->2), natomiast w drugim brakuje dwójki więc wstawimy 5 (2<->4 i 4<->5).
Wygenerowane w ten sposób dzieci będą wyglądały następująco:
Pierwsze: 1-4-3-5-2, drugie 5-2-3-4-1. - Krzyżowanie z pożądkowaniem (OX)
W tym krzyżowaniu potomków tworzy się na podstawie podtras pobranych z rodziców (podtrasa pierwszego dziecka pobierana jest z drugiego rodzica natomiast podtrasa drugiego dziecka z pierwszego). Następnie uzupełnia się trasy miastami pobranymi z drugiego rodzica z zachowaniem pożądku z pominięciem miast już wykorzystanych. Przykład:
Rodzic pierwszy: 3-2-1-4-5, rodzic drugi: 2-4-3-5-1, pozostawiana podtrasa: miasta od 2 do 4:
Pierwsze dziecko: x-4-3-5-x, drugie dziecko x-2-1-4-x
Teraz uzupełniamy pierwsze dziecko: x-4-3-5-2 (ominęliśmy 5 i 3 ponieważ te miasta już występują) -> 1-4-3-5-2.
I drugie dziecko: x-2-1-4-3 (ominęliśmy 1, 2 i 4 ponieważ te miasta już występują) -> 5-2-1-4-3.
Jeśli chodzi o mutację to sytuacja jest bardzo podobna: w zależności od rodzaju reprezentacji można zastosować standardowe operatory mutacji, bądź jakieś bardziej wyrafinowane. W przypadku reprezentacji 'naturalnej' najprostrzym rodzajem mutacji jest wymiana ze sobą dwóch miast w rozwiązaniu. Np:
1-2-3-4-5 -> wymiana miast 2 i 4 -> 1-4-3-2-5
Można również zmieniać kolejność przechodzenia miast. Np:
1-2-3-4-5 -> Zmiana kolejności w obrębie miast 1 i 4 -> 4-3-2-1-5
Można również przesunąć jakieś miasto (lub grupę miast) w ramach rozwiązania. Np:
1-2-3-4-5 -> Wstawienie miasta 1 pomiędzy 4 i 5 -> 2-3-4-1-5
Dla drugiej reprezentacji taka zabawa jest niepotrzebna ponieważ w tym przypadku mutacja sprowadza się do zamiany wartości z pozycji i losową wartością z przedziału od 1 do n-i+1 (n - liczba wszystkich miast).
I tak mniej więcej wyglądają poszczególne elementy algorytmu genetycznego rozwiązującego problem komiwojażera. Oczywiście ten tekst nie wyczerpuje w całości tego zagadnienia (istnieją jeszcze inne sposoby reprezentacji rozwiązania, istnieją inne rodzaje mutacji, krzyżowania), ale mam nadzieję, że ludziom którzy chcą po prostu gdzieś wykorzystać algorytmy genetyczne przyda się, jako krótkie przedstawienie praktyczego wykorzystania. Więcej na temat rozwiązywania problemu komiwojażera można znaleźć w [I].
Programowanie genetyczne...
Programowanie genetyczne jest próbą stworzenia systemu, który wykorzystując mechanizmy algorytmów genetycznych, będzie tworzył programy komputerowe. Ogólny zarys algorytmu genetycznego jest taki sam jak np. przy znajdowaniu optymalnej ścieżki komiwojażera. Zmieniają się tylko poszczególne elementy składowe:- Populację w tym wypadku stanowią przykładowe programy komputerowe, z których każdy wykonuje jakieś działanie.
- Krzyżowanie i mutacja tworzą nowe osobniki na podstawie już istniejących (nic się nie zmienia w porównaniu z typowym AG, należy jedynie pamiętać o zastosowaniu operatora odpowiedniego do reprezentacji)
- Funkcja oceny ma zadecydować, czy dany program chodziaż w przybliżeniu wykonuje te działania o które nam chodzi. Np. jeśli chcemy stworzyć program, który zawsze będzie znajdywał drogę wyjścia z labiryntu funkcja oceny będzie sprawdzała jak daleko 'zaszedł' dany program. Te programy, który znajdują poprawne wyjście otrzymują najwięcej punktów, natomiast te, które od wyjścia się oddalają otrzymują tych punktów najmniej.
Populacja - reprezentacja pojedynczego rozwiązania
W przypadku programowania genetycznego najczęściej stosowaną reprezentacją pojednynczego rozwiązania jest struktura drzewiasta. Jest ona bardzo wygodna z punktu widzenia krzyżowania i mutacji, a poza tym wymusza kolejność przechodzenia przez węzły i liście. Jest to reprezentacja o zmiennej długości ponieważ przykładowymi programami mogą być zarówno program wykonujący sumę dwóch argumentów jak i program obliczający pierwiastki równania kwadratowego.
Przykładowy program może wyglądać następująco:

Wynikiem działania każdego programu jest pewna wartość. Aby ją wyznaczyć należy drzewo przeglądać wstecznie (przed wykonaniem działania zapisanego w węźle należy najpierw obliczyć wyrażenia 'zaczepione' w jego dzieciach). Wartość zwracana przez powyższe drzewo jest określona wzorem:
(X*((5.00+X)-((((X-X)-(X*X))+(1.00-2.00))+(7.00-(7.00-5.00)))))
Elementami takiego drzewa mogą być:
- Jako węzły:
* Operatory arytmetyczne (+,-,/,...)
* Operatory logiczne (&&,||,!,...)
* Operatory bitowe (&,|,~,...)
* Porównania (>,<,==,...)
* Funkcje (trygonometryczne, potęgowe,...)
* Instrukcja warunkowa - IF (jeśli spełniony jest warunek (pierwszy argument), wykonywane jest poddrzewo drugiego argumentu, jeśli nie trzeciego)
* Instrukcja iteracyjna - FOR (pierwszy argument podaje ile razy ma zostać wykonane poddrzewo drugiego argumentu)
- Jako liście
* Wartości stałe, zmienno- lub stałoprzecinkowe (np.: 5, 10.5, -11)
* Wartości zmiennych (np.: X)
* Wywołania funkcji (np.: WczytajZnakZKlawiatury(), lub random())
* Wywołania procedur (np.: printf(), clrscr()) - W przypadku procedur problemem jest zwracana przez nie wartość (każdy element drzewa musi coś zwracać swojemu rodzicowi) - najczęściej przyjmuje się, że procedury zwracają zero.
Populacja początkowa wypełniona jest programami wygenerowanym całkowicie losowo. Podczas losowania osobników dobrze jest zadbać o to, aby osobniki nie były zbyt 'rozrośnięte'. Można to zrobić ustalając maksymalną głębokość lub liczbę wierzchołków tworzonego drzewa.
Krzyżowanie
Krzyżowanie polega na wymianie pomiędzy dwoma osobnikami wybranych losowo poddrzew. Poniżej przedstawiony jest przykład krzyżowania (ramką zaznaczone zostały wymieniane poddrzewa):
Sytuacja przed krzyżowaniem:
Pierwszy rodzic:

Drugi rodzic:

Sytuacja po krzyżowaniu:
Pierwsze dziecko:

Drugie dziecko:

Mutacja
Najczęściej stosowaną mutacją w przypadku programowania genetycznego jest usunięcie z osobnika losowego poddrzewa i na jego miejsce wygenerowanie nowego. Poniżej znajduje się przykład takiej mutacji (ramką zastało zaznaczone poddrzewo usuwane oraz dodawane):
Osobnik przed mutacją:

Osobnik po mutacji:

Innym sposobem mutacji jest zmiana operatowa w dowolnym wierzchołku drzewa. Należy tutaj pamiętać, że jeśli nowy operator ma mniej argumentów niż oryginalny (max(a,b)->sin(a)) należy usunąć nadmiarowe poddrzewa. Jeśli natomiast nowy operator ma więcej argumentów (max(a,b)->if(a,b,c)) należy dogenerować brakujące poddrzewa.
Można również mutować liście w drzewie. Jest to najprostrzy rodzaj mutacji (nie trzeba dodawać nowych, ani usuwać starych poddrzew), jednak powoduje niewielką zmianę działania programu jaki mutowany osobnik reprezentuje. Ten sposób mutacji przydaje się gdy rozwiązanie (osobnik, program) działa 'z grubsza' poprawnie a trzeba zmienić tylko jakieś współczynniki (np. zmiana liczby iteracji, próg do porównania dla instrukcji IF, itp.)
Funkcja oceny
Głównym zadaniem funkcji oceny jest sprawdzenie czy dany osobnik wykonuje taki program o jaki nam chodziło. W zależności od tego jak bardzo wyniki programu przypominają to o co nam chodziło osobnik dostaje odpowiednią liczbę punktów. Np dla rozwiązywania zadania aproksymacji funkcji funkcja oceny sprawdza jak daleko wygenerowana funkcja odbiega od punktów bazowych.
Do funkcji oceny warto jest dodać pewną karę za wielkość osobnika. Dzięki temu poszczególne osobniki nie będą się nadmiernie rozrastać. W przypadku drzewowej reprezentacji rozwiązania można wprowadzić karę za liczbę wierzchołków oraz karę za maksymalną głębokość drzewa.
Selekcja
Ta część algorytmu jest dokładnie taka sama jak w przypadku innych wykorzystań algorytmów genetycznych. Zarówno koło ruletki jak i metoda turniejowa bazują tylko na wartościach funkcji oceny (do działania nie potrzebują informacji o osobnikach).
Iteracyjne wykonywanie wszystkich kroków AG prowadzi do otrzymania programu (przynajmniej w przybliżeniu) rozwiązującego zadany problem. Niestety (na szczęście?) program wygenerowany dzięki programowaniu genetycznemu jest daleki od optymalnego (dlatego, póki co, programiści nie stracą pracy). Zaletą progamowania genetycznego jest fakt, że tworzenie programu w ten sposób nie wymaga żadnych nakładów pracy ze strony programisty.
Tutaj mamy program "Genetyk" za pomocą którego możemy sprawdzić na własne oczy działanie programowania genetycznego. Program ten próbuje znaleźć wzór funcji przechodzącej przez zadane punkty (aproksymacja).
Bibliografia...
- "Algorytmy genetyczne+struktury danych=programy ewolucyjne"
Zbigniew Michalewicz
Wydawnictwa Naukowo-Techniczne, 1996 - "Algorytmy genetyczne i ich zastosowania"
David E. Goldberg
Wydawnictwa Naukowo-Techniczne, 1998 - "Sieci neuronowe, algorytmy genetyczne i systemy rozmyte"
Danuta Rutkowska, Maciej Piliński i Leszek Rutkowski
Wydawnictwo Naukowe PWN, 1997
