Ogólnie (i chaotycznie) o sieciach neuronowych...
Na pewno każdy oglądał taki film co się Terminator nazywał. I taki T800 to jest w sumie to do czego dążę podczas moich badań (ale ja nie będę pracował dla wojska). No dobra żarty na bok bo to poważna sprawa.To że ludzki umysł wygrywa z komputerem w prawie wszystkich dziedzinach nie jest chyba dla nikogo nowością. Oczywiście żaden z nas nie podtrafi udzielić odpowiedzi na pytanie ile jest 8934.12*34.45/(cos(45.12)+2), komputer zrobi to bez problemu. Ale np. jeśli się nie określi dokładnie np. operatora + (to znaczy dodawanie) to się komputer wyłoży. A nam nikt nie implementował operatora +. My na podstawie wzorców uczących wyłapaliśmy, że jak mamy przed oczami 2+2=4 albo 1+5=6 albo wiele innych to taki plusik coś może oznaczać i nasz mózg się go zaczął uczyć. Ze wszystkich wzorców jakie mu zapodaliśmy na wejście wyłapał regułę z jaką działa taki plusik i teraz nasz mózg potrafi dodawać wszystkie liczby, a nie tylko te które pojawiły się w zbiorze uczącym. Sztuczne sieci neuronowe próbóją robić to co nasz mózg. To znaczy nie mają dokadnie określonego algorytmu działania... Najpierw dostają na wejście jakieś wzorce (tzw. zbiór uczący), a póżniej w czasie normalnej pracy dostają na wejście sygnał który nie był w zbiorze uczącym. I jeśli sieć jest dobrze nauczona to go poprawnie zklasyfikuje (to znaczy zrobi z nim to co powinna-tak jak my pięknie potrafimy dodawać).
Powyższe wyjaśnienie jest trochę zagmatwane, więc pozwolę sobie na drobny przykładzik.
Oto on:
Acha nie napisałem jeszcze jak wygląda sztuczna sieć neurnonowa.
Na razie przyjmijmy dla uproszczenia, że jest to czarna skrzynka do której dochodzą jakieś sygnały wejściowe i wychodzą jakieś wyjściowe.
No więc nasza sieć ma zrealizować coś takiego:
we: 0 -> wy 1
we: 2 -> wy 1
we: 3 -> wy 1
we: 5 -> wy 1
we: 6 -> wy 1
we: 7 -> wy 0
we: 8 -> wy 0
we: 9 -> wy 0
we: 12 -> wy 0
we: 18 -> wy 0
To znaczy że jak na wejściu pojawi się np. 3 to na wyjściu chcemy 1. Łatwo wywnioskować, że sieć dla sygnałów mniejszych od 7 ma dać na wyjściu 1 a dla większych 0. Oznacza to że jak powyższy zbiór uczący dobrze nauczy sieć to jak jej póżniej zapodamy na wejście np 11 to dostaniemy 0.
Oczywiście funkcję realizowaną przez tą sieć można bardzo łatwo zaimplementować jako zwykłą procedurkę jakiegoś bylejakiego języka (np.:
int xxx(int l){return(l<7);}//przykładzik w c, bo lubie ten język).
I to by było dobre, ale do czasu. Bo np. możemy wpaść na pomysł, żeby zmienić zbiór uczący (np. chcemy przesunąć próg np. na 17-tke). W przypadku sieci wystarczy powtórzych proces nauki (nie ingerujemy w kod programu). Poza tym sieć neuronowa może uczyć się w trakcie pracy (program jest w tym wypadku sztywny). Dodatkową zaletą sieci jest to że potrafi wyłapać cechy charakterystyczne bardzo zawiłej funkcji (to co podałem powyżej to tylko trywialny przykład) (Przydaje się to podczas aproksymacji jakiejś funkcji, gdy mamy tylko kilka jej punktów charakterystycznych).
Mam nadzieję, że powyższe opowieści przynajmniej po części wyjaśniły o co chodzi w sieciach... (jak nie to proszę o zapytania...)
A teraz zajmijmy się tym "czarnym pudełkiem"...
No więc najprostrza sieć neuronowa to... pojedynczy neuron... A czym jest taki neuron... No więc jest to coś co ma wiele wejść i jedno wyjście. Każde wejście ma jakąś wagę.. I neuronik na wyjściu daje sygnał opisany wzorem:
z=w1*x1+w2*x2+w3*x3+......+wn*xn-w0
gdzie: - n oznacza liczbę wejść,
- x(1-n) to poszczególne wejści,
- w(1-n) to wagi poszczególnych wejść.
Drobnego wytłumaczenia wymaga ostatni składnik powyższej sumy. Mianowicie w0 to waga sztucznie stworzonego wejścia, które ma zawsze wartość -1. To wejście jest po coś potrzebne (mądre książki tak mówią...).
Ale takie 'z' to sobie może mieć w sumie bardzo różne wartości (w zależności od wag i sygnałów wejściowych). No i trzeba wyjście neuronika trochę znormalizować... Więc tak obliczone z przepuszczamy jeszcze przez tzw. funkcję aktywacji. W najprostrzym przypadku jest to funkcja progowa opisana wzorem:
y=(z<0)?0:1; //znowu C (jak ktoś nie rozumie to objaśniam: jeśli z jest mniejsze od 0 to y jest równe 0 jak jest większe to y jest równe 1)
Proces nauki polega na zapodawaniu na wejście neuronu wzorców (zbioru uczącego) i odpowiedniej korekcji wag aż do otrzymania zerowego błędu dla wszystkich wzorców.
Wydawać by się mogło, że taki biedny neuronik co to umie tylko dodawać i mnożyć nie jest w stanie zaszaleć... Nic bardziej błędnego. Otóż pojednyczy neuron potrafi klasyfikować obrazy liniowo separowalne. Takie jak np. ten przykład powyższy... W przykładnie powyższym mieliśmy tylko jedno wejście. Oczywiście można liczbę wejść zwiększać w nieskończoność. Oznacza to, że klasyfikować można punkty na płaszczyźnie, czy przestrzeni...itd... Robi wrażenie... nie...
Kiedy do mnie dotarła idea/istota działania pojedynczego neuronu z progową funkcją aktywacji to ochoczo zabrałem się do sieci od strony praktycznej. No i wygenerowałem programik który obrazuje klasyfikacj ę pojedynczego neuronu. Rysujemy na płaszczyźnie punkty należące do dwóch różnych klas (to jest nasz zbiór uczący) i uczymy neuronik (dwa wejścia jedno wyjście). Po nauce programik pokazuje jak się neuronik nauczył (pokazana jest linia decyzyjna która oddziela od siebie obszary z obu klas). Gdybyśmy na wejście tak nauczonego neuronu zapodali jakiś punkt który nie był w zbiorze uczącym to neuronik by go poprawnie sklasyfikował. Programik ten jest w dziale: 'Trochę mojego kodu'.
A teraz wyjaśnię znaczenie zwrotu "liniowo separowalne". Oznacza to że jeśli chcemy klasyfikować np. punkty na płaszczyźnie to musi istnieć linia prosta, która dzieli cały obszar na dwa półobszary. W jednym będą znajdować się obrazy z jednej klasy a w drugiej z drugiej (nauczanie neuronu to właśnie szukanie tej lini decyzyjnej). Jeśli obrazy nie będą liniowo separowalne to pojedynczy neuronik się tego nie nauczy...:(... (Jeśli byśmy sobie do poprzedniego przykładu dodali następującą parę uczącą: we: 13 -> wy 1 to pojedynczy neuronik by sobie nie dał rady...) . Innym przykładem jest funkcja XOR:
we1:0 we2:0 -> wy:0
we1:0 we2:1 -> wy:1
we1:1 we2:0 -> wy:1
we1:1 we2:1 -> wy:0
No dobra to chyba wszystko co można ogólnie powiedzieć o neuronach (oczywiście jest to tylko szczycik góry lodowej). Jeśli ktoś ma ochotę na więcej to proszę pytać...
Kilka słów o pojedynczym neuronku...
Sztuczna sieć neuronowa, jak sama nazwa wskazuje, składa się z całej gromady neuronów odpowiednio ze sobą połączonych. Tekst ten opowiada o najmniejszych elementach składowych tej sieci, czyli o neuronikach właśnie.Pojedyncze sztuczne neuronki mają być podobne do naturalnych neuronów którymi wypełniony jest nasz mózg... Niestety obecny poziom techniki, nauki itp. nie pozwala na stworzenie dokładnej kopi mózgu (to chyba dobrze...). W mózgu neuroników jest bardzo durzo, a poza tym to wszystkie neuroniki w mózgu działają równolegle.
Jednak już dawno temu udało się opracować matematyczny model neuronu, który jest okrojoną wersją neuronu naturalnego. Model ten stworzony został w 1943 przez McCullocha i Pittsa.
Model ten opisywał pewne urządzenie do którego dochodziły jakieś sygnały wejściowe (od jednego do bardzo dużo), a wychodził jeden. Wartość wyjścia była zależna od wartości sygnałów podanych na wejście oraz od wag przypisanych do wejść.
Schematyczny obrazek sztucznego neuronu:
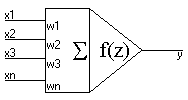
Na rysunku widać wszystkie najważniejsze elementy neuronu...
- x1-xn - sygnały wejściowe
- w1-wn - wagi wejściowe
- symbol sumy
- funkcja aktywacji
- y - wyjście
Pierwsza część neuronu oblicza sumę ważoną wejść. Oznacza to, że sygnał z opuszczający tą część jest równy:
z=w1*x1+w2*x2+...+wn*xn
Tak obliczony sygnał jest przepuszczany przez funkcję aktywacji f. Dopiero ten sygnał jest podawany na wyjście y.
O ile część piersza neuronu jest zazwyczaj taka sama (suma ważona) to funkcja aktywacji w różnych rodzajach neuronów jest różna. Poniżej przedstawiam te najczęściej spotykane:
| Funkcja liniowa W przypadku tej funkcji wielkiej filozofii nie ma: suma ważona jest bezpośrednio przepisywana na wyjście: y=z  |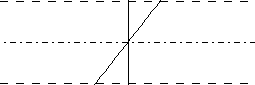
| 'Obcięta' funkcja liniowa Funkcja ta zapewnia, że sygnał wyjściowy nigdy nie będzie mniejszy niż -1 ani większy od jedynki. Dzieje się to jednak w sposób bardzo brutalny: jeżeli z<-1 to y=-1, jeżeli z>1 to y=1, w pozystałych przypadkach y=z  |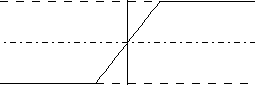
| Funkcja progowa unipolarna Tą funkcą było aktywowane wyjście w modelu McCullocha i Pittsa. Funkcja jest bardzo prosta: y=0 gdy z<0 y=1 gdy z>=0 Dzięki swojej prostocie neurony z progową funkcją aktywacji są wdzięcznym przykładem przy omawianiu algorytmów nauki sieci (o nauce takiego neuronu będzie opowiadał mój kolejny tekst, ale kiedy ujrzy światło dzienne to się jeszcze zobaczy)  |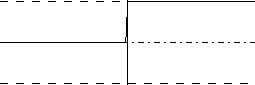
| Funkcja progowa bipolarna Funkcja w zasadzie taka sama jak powyższa - zmienia się tylko zakres wartości: y=-1 gdy z<0 y=1 gdy z>=0  |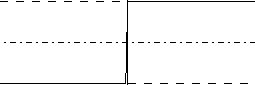
| Funkcja sigmoidalna unipolarna Funkcja ta jest najczęściej wykorzystywana przy budowie sieci. Opisana jest następującym wzorem: y=1/(1+exp(-beta*z)) Sam wzór jest bardzo skomplikowany jednak jego pochodna jest bardzo prosta do wyznaczenia. Dzięki temu proces nauki jest bardzo prosty... We wzorze pojawia się współczynnik beta. Jego wartość określa 'ściśnięcie' wykresu. Im beta mniejsze tym wykres bardziej ściśnięty, przy beta rosnącym do nieskończoności wykres pokrywa się z wykresem funkcji progowej.  |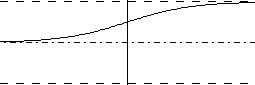
| Funkcja sigmoidalna bipolarna Funkca jest drobnym przetworzeniem powyższej. Dzięki temu został rozszerzony przedział wartości wyjścia (-1,1): y=2/(1+exp(-beta*z))-1  |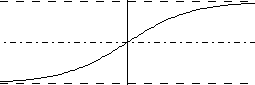
| Tangens hiperboliczny Funkcja wyglądem przypomina poprzedną, jednak wzór jest zupełnie różny: y=(1-exp(-alfa*z))/(1+exp(-alfa*z)) |
To chyba wszystkie funkcje aktywacji z jakimi do tej pory się spotkałem.
Chciałbym teraz powrócić do budowy neuronu i opowiedzieć o bardzo ważnej rzeczy.
Aby neuron mógł nauczyć się każdej funkcji separowalnej liniowo (co to znaczy zaraz napiszę), musi istnieć jeszcze jedno wejście, które jest połączone do jakiegoś stałego sygnału. Dzięki temu możliwe jest przesuwanie funkcji aktywacji (nie muszą one przechodzić przez punk 0,0). Jest to potrzebne gdzy chcemy próg aktywacji neuronu przestawić na jakąś wartość różną od zera. Dodatkowy sygnał posiada również odpowiadającą mu wagę (w0), jest również brany pod uwagę przy obliczaniu sumy ważonej wejść.
A czego potrafi nauczyć się taki pojedynczy neuronik... Jest on w stanie (po odpowiedniej nauce oczywiście) klasyfikować wielowymiarowe obrazy wejściowe do dwóch różnych klas. Jednak ze względu na fakt, że pojedynczy neuroj jest bardzo 'ubogi' potrafi klasyfikować tylko obrazy liniowo separowalne, oznacza to, że musi istnieć linia prosta która będzie oddzielała od siebie obrazy z różnych klas. To ograniczenie przełamują sieci wielowarstwowe (ale to już temat na inną pogadankę)
Na koniec chciałbym napisać, że cała 'wiedza' neurnu jest zawarta w wagach (w0-wn) i na modyfikacji tych wag polega nauka neuronu. Ze względu na fakt, że waga w0 również bierze udział w modyfikacji podczas nauki nie jest ważne jaką wartość będzie miał sygnał do którego będzie podłączona, ponieważ podczas nauki waga w0 sama ustawi się na odpowiednim poziomie.
Neuron idzie do szkoły...
Chciałbym przedstawić drogim czytelnikom prosty sposób nauki neuronu sprowadzający się w zasadzie do dodawania (i odejmowania). Nauka będzie przeprowadzana dla neuronu którego funkcja aktywacji wygląda następująco:y=-1 gdy z<0
y=1 gdy z>=0
Jest to czwarta z przedstawianych powyżej.
Przyjmijmy dla uproszczenia, że chcemy klasyfikować obszary mające tylko jeden wymiar. Dzięki temu wszystkie modyfikacje wag i ich przyczyny będzie można zobrazować na płaskim (2D) wykresie. Jeśli chcielibyśmy to samo rysować dla obrazów posiadających dwa wymiary (atrybuty) to potrzebne by nam były wykresy 3D (dla 3 wymiarów 4D - ja takich nie umiem rysować :). Należy również pamiętać o fakcie, że dla udanej nauki potrzeba do neuronu doprowadzić jakiś stały sygnał (dlatego liczba analizowanych wymiarów jest zawsze o jeden większa niż liczba atrybutów obiektów). Nasz neuronik będzie wyglądał następująco:
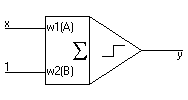Funkcja realizowana przez taki neuron wygląda następująco:z=w1*x+w2
Widać wyraźnie, że wzór ten powstaje z ogólego wzoru na prostą przechodzącą przez punkt (0,0):
0=A*x+B*y
W naszym przypadku y=1. Nauka neuronu sprowadza się do znalezienia takiego A i B, żeby wszystkie wzorce, które mają być przez neuron interpretowane jako 1 znajdowały się po dodatniej (wskazywanej przez wektor prostopadły) stronie tej prostej, natomiast te które mają zwracać -1, były po przeciwnej. Wektorem prostopadłym do tej prostej jest wektor mający współżędne równe współczynnikom przy x i y, czyli A i B, a przekładając to na neuronik są to wagi w1 i w2.
I może od razu mały przykładzik. Mamy następujący zbiór uczący:
| Wejście: | Wyjście |
| -4 | -1 |
| -1 | 1 |
| 1 | 1 |
| 3 | 1 |
Przyjmijmy, że na początku wektor wag jest równy=[3,1]. Graficzna interpretacja jest następująca (na czerwono zostały zaznaczone punkty które mają zwrócić 1, na niebiesko te które zwracają -1):
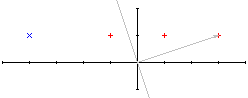
Dzięki temu, że wszystkie współżędne y są równe 1 jest możliwe znalezienie prostej przechodzącej przez początek układu współrzędnych rozdzelejącej wszystkie punkty.
Z powyższego rysunku widać, że punkty 1,3 i 4 są przez neuron dobrze klasyfikowane. Niestety dla drugiegp punktu siec zwraca -1 zamiast 1. Aby to naprawić należy zmodyfikować wektor wag dodając do niego wektor wzorca przemnożony przez pewną stałą. Stała ta powinna być równa 2*ni (źródło: [I]), gdzie ni jest współczynnikiem określającym szybkość uczenia. Do dalszych rozważań przyjmijmy ni równe 1.
Nowy wektor wag będzie więc równy:
[w]=[3,1]+[-1,1]*2=[1,3]
A tak to wygląda graficznie:
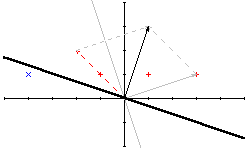
Okazuje się, że tak otrzymana linia decyzyjna (zaznaczona grubą krechą) zapewnia nam poprawne klasyfikowanie wszystkich wzorców.
A co zrobić w przeciwnym przypadku, gdy dla jakiegoś wzorca sieć zwraca 1 zamiast -1. Odpowiedź jest bardzo prosta: jeżeli jakiś wzorzec znalazł się po dodatniej stronie wykresu, choć nie powinien to jego symetryczne odbicie (względem początku układu współrzędnych) powinno się tam znaleźć. Z tego wynika, że w takim przypadku też trzeba do wektora wag dodać podwojony wektor wzorca, ale z przeciwnym znakiem. Obrazuje to przykład:
Przed modyfikacja mamy następującą sytuację (punkt niebieski: 1,1; punkt czerwony 2,1; początkowy wektor wag: [4,-1]):
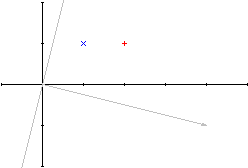
Nowy wektor wag będzie więc równy:
[w]=[4,-1]-[1,1]*2=[2,-3]
Graficzna interpretacja:
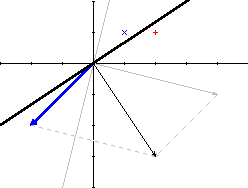
W ten sposób otrzymaliśmy linię decyzyjną, która poprawnie rozpoznaje nam wzrorce.
Podsumowując: celem nauczenia neuronu dowolnych wzorców (oczywiście muszą być liniowo separowalne) należy na wejście neuronu podawać po kolei wszystkie wzorce i sprawdzać, czy oczekiwane wyjście jest równe od otrzymanego. Gdy warunek ten nie jest spełniony należy skorygować wagi:
[w1,w2]nowe=[w1,w2]stare+2*[x,y], gdy otrzymano -1 dla 'dodatniego' wzorca
lub
[w1,w2]nowe=[w1,w2]stare-2*[x,y], gdy otrzymano 1 dla 'ujemnego' wzorca
Można to uogólnić:
[w1,w2]nowe=[w1,w2]stare+2*{oczekiwane wyjście}*[x,y]
Gdy po n iteracjach okarze się, że wszystkie wzorce zwracają to co powinny możemy zakończyć naukę neuronu.
I mały przykładzik:
Mamy następujące wzorce:
- punkty niebieskie: [-1,1][1,1], dla których sieć ma zwracać -1
- punkt czerwony: [3,1] ,dla którego sieć ma zwracać 1
Początkowe wartości wag: w1=3,w2=1.
Na wykresie wygląda to następująco:
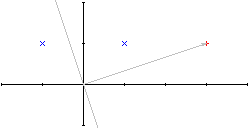
Krok 1
Sieć niepoprawnie klasyfikuje punkt 2 - oczekiwane wyjście: -1, otrzymane: 1
Modyfikacja wektora wag: [w]=[3,1]-2*[1,1]=[1,-1]
Wykres
Krok 2
Proszę zauważyć (patrz poprzedni wykres), że punkt 2 leży na lini decyzyjnej. Gdybyśmy mieli trochę inną funkcję aktywacji, która dla sumy ważonej równej 0 zwracałaby -1 to na tym kroku moglibyśmy zakończyć naukę. Nasza funkcja aktywacji wymaga jednak wartości sumy ważonej ostro mniejszej od zera.
Modyfikacja wektora wag: [w]=[1,-1]-2*[1,1]=[-1,-3]
Wykres
Krok 3
Sieć niepoprawnie klasyfikuje punkt 3 - oczekiwane wyjście: 1, otrzymane: -1
Modyfikacja wektora wag: [w]=[-1,-3]+2*[3,1]=[5,-1]
Wykres
Krok 4
Sieć niepoprawnie klasyfikuje punkt 2 - oczekiwane wyjście: -1, otrzymane: 1
Modyfikacja wektora wag: [w]=[5,-1]-2*[1,1]=[3,-3]
Wykres
Krok 5
Podobna sytuacja jak w kroku 2. Linia decyzyjna przechodzi przez punkt 2.
Modyfikacja wektora wag: [w]=[3,-3]-2*[1,1]=[1,-5]
Wykres
Krok 6
Sieć niepoprawnie klasyfikuje punkt 3 - oczekiwane wyjście: 1, otrzymane: -1
Modyfikacja wektora wag: [w]=[1,-5]+2*[3,1]=[7,-3]
Wykres
Krok 7
Sieć niepoprawnie klasyfikuje punkt 2 - oczekiwane wyjście: -1, otrzymane: 1
Modyfikacja wektora wag: [w]=[7,-3]-2*[1,1]=[5,-5]
Wykres
Krok 8
I znowu powtarza się sytuacja z kroków 2 i 5
Modyfikacja wektora wag: [w]=[5,-5]-2*[1,1]=[3,-7]
Wykres
Krok 9
Tym oto sposobem otrzymaliśmy prostą, która rozdziela nam punkty niebieskie od czerwonych. W sumie były tylko trzy wzorce, a musieliśmy wykonać, aż osiem iteracji... Proszę zauważyć, że z liczbą iteracji maleje kąt o jaki zmienia się linia decyzyjna. Dzięki czemu może ona coraz dokładniej wpasowywać się pomiędzy wzorce. Dzieje się to dzięki stopniowemu wydłużaniu się wektora prostopadłego (dlatego do wag był dodawany wektor wzorca przemnożony przez współczynnik, gdyby tego współczynnika nie było zmiany wektora w kolejnych iteracjach znosiłyby się).
Aby rozszerzyć możliwości neuronika o rozpoznawanie obrazów mających więcej wymiarów (atrybutów) należy dodać do niego kilka dodatkowych wejść (po jednym na każdy atrybut). Procedura nauki wogóle nie ulegnie zmianie. Należy tylko pamiętać o modyfikacji wszystkich wag neuronika.
Na koniec chciałbym jeszcze opowiedzieć jak wykorzystać neuroniki do klasyfikacji obrazów należących do kilku różnych klas. Aby to było możliwe należy wykorzystać kilka neuroników połączonych równolegle:
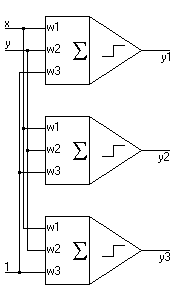
Na obrazku przedstawiony jest system, który klasyfikuje obrazki na płaszczyźnie (wejścia x i y) do trzech różnych klas (y1,y2,y3). Podobnie jak w przypadku pojedynczego neuronu poszczególne klasy muszą być liniowo separowalne (z tym ograniczeniem zrywają dopiero sieci warstwowe). Np:
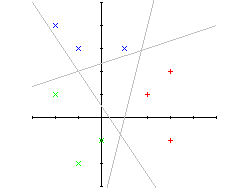
Proszę zauważyć, że każdy z tych neuronów możemy analizować osobno (wyjście jednego neuronu nie zależy od zachowania się pozostałych - ważny jest tylko poziom sygnału wejściowego). Dlatego proces nauki możemy przeprowadzić osobno dla każdego z nich w ten sam sposób w jaki robiliśmy to powyżej. Poprawnie nauczony neuron jest aktywny (ma wartość 1) gdy na wejściu pojawia się sygnał należący do klasy którą ten neuron rozpoznaje i jest nieaktywny (wartość -1) gdy na wejściu jest coś innego.
ps. A tutaj mamy program przedstawiający naukę neuronu ze skokową funkcją aktywacji: Siec.rar - 45291 bajtów
Neuron sigmoidalny idzie do szkoły (a za nim cała sieć neuronowa)...
Powyższy tekst opowiadał o nauce neuronu o skokowej funkcji aktywacji. Teraz zajmiemy się nauką neuronu z bardziej wyrafinowaną funkcją aktywacji. Opisana poniżej metoda nauki obowiązuje dla wszystkich neuronów, których funkcja aktywacji jest różniczkowalna. Jednak cały opis będzie oparty na funkcji sigmoidalnej, ponieważ taka funkcja jest wykorzystywana najczęściej w praktycznych zastosowaniach.Na początku może kilka oznaczeń używanych później:
x0,x1,x2,x3,.... - Wartośći sygnałów wejściowych (x0 zawsze podłączony jest do stałej wartości - patrz tekst na temat pojedynczego neuronu)
w0,w1,w2,w3,.... - Wagi przypisane kolejnym wejściom
z - Suma ważona sygnałów wejściowych (z=x0*w0+x1*w1+x2*w2+.....)
f() - Oznaczenie funkcji aktywacji
y - Wyjście neurnonu (suma ważona przepuszczona przez funkcję aktywacji - y=f(z))
o - Oczekiwane wartość wyjścia neuronu
Podczas nauki pojedynczego neurnou na wejście podawane są poszczególne wartości ze zbioru uczącego. Na podstawie tego sygnału generowane jest wyjście neuronu porównywane z wartością oczekiwaną. Zadaniem neuronu jest udzielenie odpowiedzi takiej samej jak odpowiedź spodziewana. Miarą błędu dla pojedynczego neuronu jest zatem różnica pomiędzy oczekiwanym wyjściem a otrzymanym. Dla całego zbioru uczącego całkowity błąd będzie sumą błędów pojedynczych wzorców.
Ze względu na fakt że błędy mogą być dodatnie i ujemne w końcowym rozrachunku mogą się znosić i dla bardzo źle nauczonego neuronu otrzymamy zerowy błąd całkowity dlatego jako błąd dla pojedynczego wzorca brany jest kwadrat różnicy sygnałów:
E=(o-y)^2
(w późniejszych przekształeceniach będziemy wykorzystywali wzór na błąd następującej postaci:
E=((o-y)^2)/2
wartość 1/2 pojawia się tylko po to aby uprościć późniejsze obliczenia).
O ile wartość oczekiwana jest niezmienna (jest narzucona przez zbiór uczący) tak wartość błędu zależy od wartości wyjścia sieci, a ta z kolei zależy od wartości wag (przy stałych wartościach sygnałów dochodzących do neuronu). Na poniższym wykreśsie przedstawiona jest wartośc błędu w zależności od wartości wag przy x1=-0.1, x2=0.98 i oczekiwanej wartości wyjścia o=0,45:
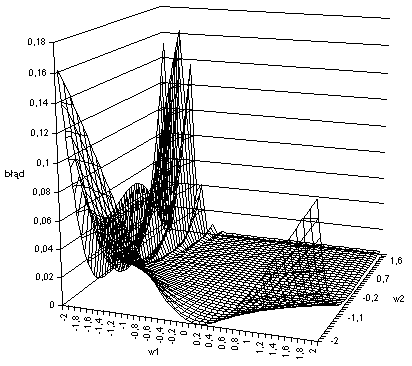
Z wykresu widać, że najmniejszy błąd jest generowany gdy wagi są ustawione na w1=0.2 i w2=-2.
Jak znaleźć te wagi startująć od dowolnych wag początkowych? Wiadomo, że kierunek największego spadku dowolnej funkcji wskazuje ujemny gradient funkcji, czyli wektor utoworzony z pochodnych po wszystkich zmiennych. Dlatego wektor wag neuronu jest przesuwany w kierunku ujemnego gradientu. Dodatkowo wektor ten jest przemnażany przez współczynnik h, który nazywany jest współczynnikiem szbkości uczenia (współczynnik korekcji). Zatem zmiana wagi w każdej iteracji jest równa:
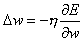Ze względu na fakt, że wartość funkcji aktywacji neuronu zależy tylko od wartości sumy ważonej, a suma ważona zależna jest od wag pochodną funkcji aktywacji możemy zapisać:
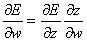Pochodna błędu po wartości sumy ważonej nazywana jest sygnałem błędu delta i oznaczana jest d. Natomiast pochodna sumy ważonej względem wagi jest równa wartości sygnału wejściowego x. Wzór na przyrost wagi jest zatem równy:w=w+h*d*x Zajmijmy się teraz wartością d. Przekształcając podstawowy wzór otrzymujemy:
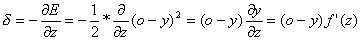A po podstawieniu do wzoru na nową wartość wagi otrzymujemy:
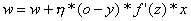Pozostaje jeszcze problem pochodnej funkcji aktywacji. Przy opisie funkcji aktywacji neuronów (w tekście opisującym pojedynczy neuron) napisałem, że funkcje sigmoidalne są wykorzystywane ze względu na proste pochodne. Okazuje się bowiem, że pochodna fuknkcji unipolarnej danej wzorem: 1/(1+exp(-z)) jest równa: y*(1-y), natomiast pochodną funkcji bipolarnej 2/(1+exp(-z))-1 jest (1-y^2)/2.Podsumowując algorytm nauki pojedynczego neuronu wygląda następująco:
1. Pobierz ze zbioru uczącego parę wejście-oczekiwane wyjście.
2. Podaj na wejście neuronu wartości wejściowe.
3. Oblicz sygnał wyjściowy neuronu.
4. Zmodyfikuj wagę każdego wejścia za pomocą wzorów:
a) wj=wj+xj*h*(o-y)*(o-y)*(1-y^2)/2 - dla bipolarnej funkcji aktywacji
b) wj=wj+xj*h*(o-y)*(o-y)*y*(1-y) - dla unipolarnej funkcji aktywacji
gdzie j=0..N (N - liczba wejść neuronu)
5. Powyższe kroki powtarzaj dla wszystkich par uczących.
6. Zakończ naukę gdy całkowity błąd dla wszystkich wzorców uczących będzie mniejszy od pewnej ustalonej na początku nauki wartości.
Podobnie jak w przypadku neuronu ze skokową funkcją aktywacji neurony sigmoidalne można ze sobą łączyć równolegle dzięki temu można rozpoznawać obrazy należące do kilku kategorii. Oczywiście cały czas pozostaje problem liniowej separowalności poszczególnych klas. Problem ten rozwiązują sieci wielowarstwowe.
Zabierzmy się zatem za naukę sieci wielowarstwowych.
Przykładowa wielowarstwowa siec neuronowa wygląda następująco:
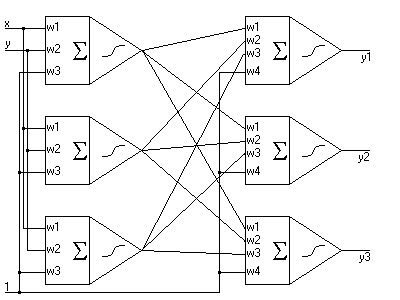
Zadaniem tej sieci jest klasyfikowanie dwuwymiarowych obrazów (wejścia x i y) do trzech różnych klas (y1,y2,y3). Na obrazku widać wyraźnie, że wyjścia neuronów z warstwy n są liczone na podstawie wyjść neuronów z warstwy n-1. Wyjątkiem od tej zasady są neurony z warstwy pierwszej (neurony wejściowe), dla których wyjścia oblicza się na podstwie sygnałów wejściowych. Takie zależności narzucają sposób obliczania wartości wyjścia całej sieci. Najpierw obliczamy wyjścia warstwy pierwszej na podstawie wejść sieci, później obliczamy wyjścia warstwy drugiej na podstawie wyjść warstwy pierwszej, itd aż do ostatniej warstwy sieci.
Nauka takiej sieci jest zbliżona do nauki pojedynczego neuronu. Wyjściowym wzorem jest:
w=w+h*d*x (gdzie x jest sygnałem wejściowym aktualnie analizowanego neuronu - dla warstwy pierwszej będą to sygnały wejściowe, dla kolejnych warstw wartości wyjściowe neuronów z warstwy poprzeniej).
Jedynym problemem w tym wzorze jest wartość d, czyli błąd neuronu. Dla pojedynczego neuronu można było tą wartość obliczyć na podstawie różnicy sygnału wyjściowego i oczekiwanego. Proszę zauważyć że w przypadku sieci wielowarstwowej takie obliczenie d jest możliwe dla ostatniej warstwy neuronów. Czyli dla warstwy wyjściowej:
d=(o-y)*f'(z) A co w takim razie z pozostałymi warstwami sieci? Okazuje się, że d dla dowolnej warstwy sieci (oprócz wyjściowej) jest równa sumie ważonej delt z warstw następnych przemnożonej przez pochodną funkcji aktywacji:
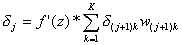gdzie:j - aktualnie analizowana warstwa neuronów
j+1 - następna warstwa neuronów
K - liczba neuronów w warstwie j+1
k - neuron z warstwy j+1
(Wyprowadzenie tej zależności znajduje się w [V], są tam też dokładnie opisane wcześniejsze zależności (dotyczące pojedynczego neuronu)). Tak obliczony błąd propagujemy przez wszystkie warstwy aż do wejściowej.
Algorytm wstecznej propagacji błędów wygląda więc następująco:
1. Pobierz ze zbioru uczącego parę wejście-oczekiwane wyjście.
2. Podaj na wejście neuronu wartości wejściowe.
3. Przepuść sygnał przez siec obliczając wyjścia poszczególnych neuronów w kolejnych warstwach.
4. Oblicz sygnał wyjściowy neuronów z warstwy wyjściowej.
5. Oblicz błędy w neuronach warstwy wyjściowej - d=(o-y)*f'(z).
6. Kożystając ze wzoru:
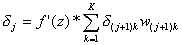przepropaguj (wstecz) błędy przez całą sieć7. Uaktualnij (w=w+h*d*x) wszystkie wagi w sieci.
8. Powyższe kroki powtarzaj dla wszystkich par uczących.
9. Zakończ naukę gdy całkowity błąd dla wszystkich wzorców uczących będzie mniejszy od pewnej ustalonej na początku nauki wartości.
Za pomocą tego algorytmu możemy nauczać sieci o dowolnej liczbie warstw. Dzięki zastosowaniu wielu warstw sieć może nauczyć się rozróżniania obrazów które nie są liniowo separowalne.
Bibliografia...
- "Wstęp do teorii obliczeń neuronowych"
John Hertz, Anders Krogh, Richard G. Palmer
Wydawnictwa Naukowo-Techniczne 1995 - "Sieci neuronowe w praktyce"
Timothy Masters
Wydawnictwa Naukowo-Techniczne 1996
- "Sieci neuronowe, algorytmy genetyczne i systemy rozmyte"
Danuta Rutkowska, Maciej Piliński, Leszek Rutkowski
Wydawnictwo Naukowe PWN 1997
- "Sieci neuronowe w ujęciu algorytmicznym"
Stanisław Osowski
Wydawnictwa Naukowo-Techniczne 1996
- "Sztuczne sieci neurnowe"
J. Żurada, M.Barski, W.Jędruch
Wydawnictwo Naukowe PWN 1996
Autor: Paweł Kopczyński