Wstępniak...
Nie będę zaczynał od zupełnych podstaw, tzn. nie będę definiował co to jest szyfr, szyfrogram itp., bo to są sprawy oczywiste i każdy człowiek z odrobiną intuicji od razu wie o co chodzi.Na początku wyjaśnię pewną sprawę. Są algorytmy, których bezpieczeństwo bazuje na utrzymywaniu istoty ich działania w tajemnicy. Takie algorytmy nazywają się algorytmami ograniczonymi. Algorytmy ograniczone odegrały wielką rolę w historii kryptografii, lecz dzisiaj zapewniany przez nie standard zabezpieczenia danych jest niewystarczający. Nie może ich używać duża lub zmienna liczba użytkowników, ponieważ mogą oni ujawnić sekret. Jeżeli to się stanie to narażone jest bezpieczeństwo całego systemu. Może jeszcze ważniejsze jest to, że złamaine takiego szyfru dla doświadczonego kryptoanalityka jest stosukowo proste. Pomimo to algorytmy takie są powszechnie stosowane w wielu systemach o małym stopniu zabezpieczenia. Z tych powodów jeśli będę pisał o odporności danego szyfru na złamania nie będę miał na myśli trudności zrozumienia jego działania. Po prostu powszechnie się przyjmuje, że przy łamaniu szyfrów algorytm szyfrowania (sposób jego działania) jest powszechnie znany.
Zacznę od podziału szyfrów. Wyróżniamy więc dwie główne grupy szyfrów:
- symetryczne,
- asymetryczne.
Symetryczny algorytm szyfrowania, to taki, w którym zarówno szyfrowanie, jak i deszyfrowanie danych odbywa się przy użyciu jednego klucza. Pod pojęciem klucza można rozumieć np. hasło, czy dużą liczbę pierwszą wygenerowaną przez komputer (zależnie od algorytmu szyfrowania), ogólnie rzecz biorąc jest to ciąg bitów. Tak więc algorytm symetryczny używa tego samego klucza do szyfrowania i deszyfrowania. Takie algorytmy mają zastosowanie w wielu dziedzinach życia np. gdy chcemy, by dane o naszych dochodach, które są przechowywane na dysku twardym, były dostępne tylko dla nas, to użyjemy do tego algorytmu symetrycznego: zaszyfrujemy dane przy użyciu jakiegoś hasła, które tylko my znamy, gdy któś chce się dobrać do naszych danych nic nie może odczytać, bo nie zna hasla. Taki mechanizm jest zastosowany w różnego rodzaju programach do kompresji danych - zipach, rarach i innych, lecz także np. w kartach bankomatowych.
Algorytmy asymetryczne (z kluczem jawnym) używają dwóch kluczy. Jeden służy do szyfrowania danych, drugi, inny służu do deszyfrowania. Ten do szyfrowania jest publicznie ogłaszany (jest też nazywany kluczem publicznym) np. w internecie, natomiast ten służący do deszyfrowania jest pieczołowicie chowany (jest on nazywany kluczem prywatnym). Taki algorytm ma zastosowanie w następującej sytuacji: my chcemy, by każdy mógł wysłać do nas list, którego nikt prócz nas nie będzie mógł odczytać; publikujemy swój klucz publiczny, zainteresowana osoba pisze do nas list, szyfruje go za pomocą naszego klucza publicznego; teraz, do odczytania wiadomości potrzebny jest klucz prywatny, którego rzecz jasna tylko my posiadamy. Przy tym algorytmi jest bardzo ważne, by nie dało się nie tylko odczytać zaszyfrowanej wiadomości, lecz także, by nie można było wywnioskować na podstawie klucza publicznego jak wygląda klucz prywatny. Taki algorytm stosuje się np. w znanym programie kryptograficznym PGP.
Zajmiemy się wpierw pierwszą grupą algorytmów szyfrowania - algorytmami symetrycznymi. Zacznijmy od początku. Przed erą komputerową kryptografia zajmowała się szyfrowaniem działającym na pojedyńczych znakach. Były to algorytmy dokonujące przestawień oraz podstawień znaków. Najlepsze rezultaty osiągano mieszając wielokrotnie te dwie techniki. Gdy nadeszły komputery zmianie uległ jedynie alfabet: z 26 znaków zrobiły się 2 (1 bit, dwa stany: 0 i 1). Większość dobrych dzisiejszych komputerowych algorytmów symetrycznych nadal łączy technike przestawienia z podstawianiem (są wyjątki ofcoz).
Szyfr podstawieniowy to taki, w którym każdy znak w tekście jest zastąpiony innym znakiem (ma to sens jedynie przy dość dużym alfabecie np. 26-znakowym). Podstawienie powoduje, że tekst jawny nie jest zrozumiały dla nikogo oprócz odbiorcy, który odwraca podstawianie i uzyskuje tekst jawny. W kryptografii wyróżnia sie cztery podstawowe typy szyfrówpodstawieniowych:
- Prosty szyfr podstawieniowy, w którym każdy znak tekstu jawnego jest zastępowany odpowiednim znakiem.
- Homofoniczny szyfr podstawieniowy jest podobny do prostego szyfru podstawieniowegoz tym, że pojedyńczemu znakowi tekstu jawnego jast przyporządkowanych kilka znaków. Na przykład literze "A" może odpowiadać 5,13,25,56, literze "B" - 7,19,31,42 itd.
- Wieloalfabetowe szyfry podstawieniowe są złożeniem wielu prostych szyfrów podstawieniowych. Zmiana alfabetu może na przykład następować wraz z pozycją znaku w szyfrowanym tekście.
- Poligramowy szyfr podstawieniowy to taki, w którym są szyfrowane grupy znaków. Na przykład trójce "ABA" odpowiada "RTQ", a "ABB" opowiada "SSL" itd.
Słynnym przykładem prostego syfru podstawieniowego jest szyfr Cezara. W nim każdy znak tekstu jawnego jest zastępowany znakiem przesuniętym w alfabecie o trzy miejsca w prawo względem znaku źródłowego ("A" jest zastępowane przez "D", "B" przez "E", "X" przez "A" itd.). Innym przykładem prostego szyfru przestawieniowego jest programik dostarczany wraz z systemem UNIX ROT13. Algorytm ten różni się tym od szyfru Cezara, że przesunięcie jest równe 13, a nie 3. Ma to tę własność, ten sam program może szyfrowac i odszyfrowywać daną wiadomość (dlatego, że alfabet ma 26 znaki i podwójna rotacja znaków o 13 daje wyjściowy tekst). Łamanie tego typu szyfrów jest stosunkowo proste (w porównaniu do innych systemów kryptograficznych), a to dlatego, że szyfry podstawieniowe nie zmieniają właściwości statystycznych występowania danego znaku. Oznacza to, że badając częstotliwość występowania danego znaku możemy z dużym prawdopodobieństwem go odtworzyć. Litery alfabetu nie występują bowiem z jednakową częstotliwością - analiza tych częstotliwości w zaszyfrowanych tekstach pozwala na złamanie szyfru. Dla przykładu przyjrzymy się przeciętnej częstotliwości występowania liter w tekstach w języku angielskim. Najczęściej spotykaną literą jest "E" i obejmuje około 12,3% wszystkich wystąpień. Na drugim biegunie leżą litery takie jak "Y","B","G","V","K","Q","X","J","Z". Każda z nich występuje z częstotliwością poniżej 2%. Ostatnie cztery litery mają nawet częstości nie przekraczające 0,2%! Grupa liter o częstotliwościach powyżej 6% też nie jest liczna i zawiera, prócz wspomnianej litery "E", jedynia "T","A","O","N","I","S","R". Kryptoanaliza polega na sporządzeniu tabeli częstotliwości występowania liter w zaszyfrowanym tekście i porównaniu go z powyższą tabelą. Na tej podstawie można, na przykłd, zlokalizować prawdopodobne występowanie liter "E","T","H",itd. Po przyjęciu hipotetycznych wartości dla tych liter, szukamy w kryptogramie (zaszyfrowanym tekście) sekwencji liter odpowiadających typowym słowom, takim jak np. "the". Pozwala to na zweryfikowanie hipoezy i przyjęcie prawidłowych wartości dla "E","T","H". To postępowanie kontunuujemy, dysponując coraz większą ilością tekstu jawnego. Te heurystyczne metody można zawrzeć w odpowiednim algorytmie komputerowym, który będzie to robił automatycznie. Dzisiejsze programy komputerowe potrafią odszyfrować szyfrogram wyprodukowany przez algorytm podstawieniowy w ciągu kilku chwil. Homofoniczne szyfry podstawieniowe są znacznie trudniejsze do złamania niż proste szyfry podstawieniowe, lecz nadal nie zamazują statystycznych właściwości tekstu jawnego. Łamanie ze znanym tekstem jawnym (jest to sytuacja, gdy mamy kilka szyfrogramów, mamy też jeden komplet szyfrogram-tekst jawny i chcemy rozszyfrować wszystkie pozostałe szyfrogramy) jest wyjątkowo proste. Łamanie bez znanego tekstu jawnego jest trudniejsze, lecz programy kmputerowe robią to w kilka sekund. Trzeba tu dodać, że homofoniczne szyfry były już używane w 1401 r. przez księcia Mantui. Wieloalfabetowe szyfry podstawieniowe zostały wprowadzone przez Leona Battistę w 1568 r. Były używane przez armię Konfederatów podczas wojny domowej w USA. Nie bacząc na to, że szyfry te można łatwo złamać (zwłaszcza przy użyciu komputerów), stosuje je wielu producentów komercyjnych programów i urządzeń do zabezpieczania danych komputerowych. Przykładem może być tu program Word Perfect, który stosuje ten właśnie szyfr i został bardzo szybko złamany. Sposobem na utrudnienie analizy częstotliwości jest szyfrowanie poprzez podstawianie nie pojedyńczych liter ale bloków liter określonej długości. Mamy wtedy bowiem do czynienia z mniejszymi dysproporcjami w zakresie średniej częstotliwości występowania poszczególnych konfiguracji liter w bloku; w szczególności prawdopodobieństwa te stają się stosunkowo małymi liczbami. Utrudnia to odgadnięcie wartości podstawienia. W szczególności kryptoanaliza wymaga dużo dłuższych kryptogramów, aby móc skorzystać z jakichkolwiek statyustycznych prawidłowości. Takim szyfrem jest np. szyfr Playfair, wprowadzony w 1854 r., był stosowany przez brytyjczyków w czasie I wojny światowej. Jest to prosty system, w którym wszelkie operacje szyfrowania i deszyfrowania mogą być z łatwością przeprowadzone ręcznie. System gwarantuje tylko bardzo niewielki zakres bezpieczeństwa i może być traktowany jako dygresja w stronę metod historycznych. Szyfrowaniu podlegają pary znaków, przy czym używamy 25 liter (25 dużych liter alfabetu angielskiego, jedna litera, mianowicie "J", jest w tekstach zastępowana przez "I"). Do szyfrowania i deszyfrowania używany jest kwadrat 5x5, w którym wpisujemy kolejne litery występujące w haśle. Przyjmijmy, że hasło brzmi: "POSZŁA MAŁPA DO PIWNICY". Podczas wypełniania kwadratu pomijamy litery, które już raz wystąpiły. Gdy po wpisaniu tych liter zostały jeszcze wolne miejsca w kwadracie, to wypełniamy je jeszcze niewykorzystanymi literami w kolejności alfabetycznej. W ten sposób wypełniamy kwadrat 25 literami. Przy naszym haśle kwadrat wygląda tak:
P O S Z L
A M D I W
N C Y B E
F G H K Q
R T U V X
Szyfrowanie przebiega następująco. Załóżmy dla przykładu, że chcemy zaszyfrować parę "OH" według naszego klucza (wypełnionego kwadratu). Litery "O" oraz "H" wyznaczają prostokąt w kadracie do szyfrowania, w którego pozostałych rogach znajdują się "S" i "G". Reguła szyfrowania mówi, że "OH" zastępujemy właśnie tymi literami tj. "SG". Gdy para liter, jaką zamierzamy zaszyfrować, leży w jednej kolumnie lub w jednym wierszu (i wobec tego nie definiuje prostokąta), to litery te zastępujemy parą liter leżącą na prawo od nich, na przykład "SY" zastępujemy przez "ZB", parę "WE" zaś przez "AN" (litery z ostatniej kolumny zastępujemy literami z pierwszej).
Ogólnie rzecz biorąc, podstawianie nie oparte o długie bloki lub o prostych zasadach generowania permutacji z klucza (np. w systemie Playfair można z dużym prawdopodobieństwem przewidziec ostatnie litery w kwadracie 5x5, gdyż zasada jego konstrukcji mówi, iż jest on na końcu wypełniany przez pozostałe litery w kolejności alfabetycznej, co jest wystarczająco dużą wskazówką do kryptoanalizy) może być podatne na analizę np. analizę częstotliwości. Z tego względu podstawianie należy traktować raczej ajko technikę wykorzystywaną jako element pomocniczy bardziej złożonych metod.
Powiedzmy sobie teraz coś o szyfrach przestawieniowych. Szyfr przestawieniowy to taki, w którym wszystkie znaki tekstu jawnego pojawiają się w tekście zaszyfrowanym, lecz w innej kolejności. W prostym przestawieniu kolumnowym tekst jawny jest pisany w wierszach o ściśle określonej długości, a szyfrogram jest odczytywany kolumnami (pionowo). Deszyfrowanie odbywa się przez pisanie szyfrogramu w kolumny macierzy i odczytywanie tej macierzy wierszami. Np. zaszyfrujmy tekst "COMPUTERGRAPHICSMAYBESLOWBUTATLEASTIT'SEXPENSIVE". Przyjmijmy długość wiersza równą 10. Macierz będzie wyglądać tak:
COMPUTERGR
APHICSMAYB
ESLOWBUTAT
LEASTITSEX
PENSIVE
Nasz szyfrogram będzie więc wyglądał tak: "CAELPOPSEEMHLANPIOSSUCWTITSBIVEMUTERATSGYAERBTX". Przez Niemców w czasie II wojny światowej był stosowany szyfr "ADFGVX", który jest właśnie szyfrem przestawieniowym (wraz z prostym podstawianiem). Jak na ówczesne czasy był to bardzo złożony algorytm, lecz został złamany przez francuskiego kryptoanalityka George'a Painvina. Trzeba tu jeszcze dodać, że mimo, iż w nowoczesnych systemach szyfrowania stosuje się przestawienia, to jest to nieco uciążliwe, ponieważ wymaga dużych ilości pamięci, a czasami tekstów jawnych o określonych długościach. Ze względu na to szyfry podstawieniowe są stosowane znacznie częściej od przestawieniowych. W latach dwudziestych naszego stulecia wymyślono wiele urządzeń mechanicznych, które miały zautomatyzować proces szyfrowania. Były skonstruowane z wykorzystaniem elementu zwanego rotorem. Rotor, to obracające się koło, umożliwiające podstawianie znaków "A" z "F", "B" z "U" itp. Urządzenie szyfrujące, wyposażone w wiele rotorów, realizujące szyfr Vigenere'a z bardzo długim okresem było nazywane maszyną rotorową. Maszyna taka składa się z klawiatury i kilku rotorów. Każdy z nich ma 26 pozycji i służy do wykonania prostego podstawiania. Każdy rotor reprezentuje pewną permutację alfabetu. Złożenie wielu rotorów czyni rozwiązanie bezpiecznym. Okres dla maszyny z n rotorami wynosi 26^n (26 do potęgi n), ponieważ rotory poruszają się z różnymi prędkościami. Najbardziej znana maszyną rotorową (z kilkoma ulepszeniami) jest Enigma. Była ona używana przez Niemców w czasie II wojny światowej. Szyfr Enigmy został złamany jeszcze w czasie II wojny światowej przez grupę polskich matematyków.
Zawarłem tu kilka podstawowych informacji o szyfrach i opisałem podstawowe mechanizmy tworzenia szyfrów symetrycznych. W następnym odcinku "pociągnę" dalej ten temat i opiszę kilka nowoczesnych algorytmów szyfrowania symetrycznego, takich jak DES (obecnie chyba najpopularniejszy algorytm szyfrowania symetrycznego, mający zastosowanie w bardzo wielu dziedzinach życia np. w kartach bankomatowych) ale nie tylko. Więc, następnego razu...
by YAHRO (yahro@go2.pl) na podstawie:
"Kryptografia dla praktyków", autor: Bruce Schneier,
"Kryptografia", autor: Mirosław Kutyłowski, Willy-B. Strothmann,
"Algebraiczne aspekty kryptografii", autor: Neal Koblitz.
Algorytm DES...
Zanim zaczniemy się nim zajmować na serio, zobaczmy czym się on charakteryzuje:- DES jest symetrycznym algorytmem szyfrującym (ten sam klucz jest używany do szyfrowania i deszyfrowania),
- Szczegółowy opis algorytmu DES został opublikowany. Oznacza to, że DES nie jest algorytmem ograniczonym i prawdopodobnie nie zawiera tzw. ukrytych drzwi (tak określa celowo zostawione przez twórców luki w algorytmie szyfrującym, pozwalające na częściowe lub całkowite złamanie tego szyfru bez znajomości klucza),
- DES jest typowym algorytmem "hardwarowym", tzn. przy jego budowie optymalizowano go pod względem szybkości wykonywania w układach scalonych, nie zaś przez programy komputerowe (dla porównania układy realizujące DES mają prędkość rzędu GB/sek., a dobre programy komputerowe mają prędkości rzędu MB/sek.). Jest jeszcze jeden aspekt tego, że DES jest algorytmem "hardwarowym", mianowicie znacznie łatwiej jest włamać się do systemu komputerowego i podmienić software (zostawić konia trojańskiego), niż dokonać fizycznego włamania i wymienić układy scalone.
- DES jest szyfrem blokowym, tzn. szyfruje nie pojedyńcze bity informacji po kolei (szyfry strumieniowe), lecz szyfruje bloki bitów na raz (szyfry blokowe), w tym przypadku jest to 64 bitów, przy czym w DES szyfrogram ma taką samą długość, co tekst jawny tzn. tutaj 64 bity.
- Do szyfrowania DES używa klucza długości 56 bitów (w zasadzie używa się zazwyczaj haseł 64 bitowych, to jest 8 bajtów (znaków ASCII), przy czym najstarsze bity są pomijane, co daje nam nasze 56 bitów).
- W odniesieniu do DES nie zostałuy opublikowane żadne prace dające tej metodzie solidne podstawy matematyczne. Jednak trzeba tu dodać, że algorytm ten został poddany 20 latom intensywnych badań akademickich, które nie zagroziły znacząco zastosowaniu tej metodzie w praktyce (więcej o tym jeszcze napiszę).
Wiemy już mniej więcej czego możemy się spodziewać po DES. Przejdźmy więc do opisu samego algorytmu. Jak już wcześniej zostało powiedziane klucz ma długość 56 bitów. Całe bezpieczeństwo algorytmu spoczywa na kluczu. Istnieje 2^56 (2 do potęgi 56) możliwych kluczy, przy czym niektóre z nich są gorsze od innych (powiem dokładniej o tym kiedy indziej). Ogólny szkic algorytmu wygląda następująco:
TEKST JAWNY =>
=> Permutacja początkowa =>
=> 16 identycznych cykli algorytmu =>
=> Permutacja końcowa =>
=> SZYFROGRAM
Przyjmując oznaczenia:
L(i) - lewa część danych w i-tym cyklu,
R(i) - prawa część danych w i-tym cyklu,
K(i) - 48 bitowy klucz dla i-tego cyklu,
f - oznacza szereg podstawień i permutacji oraz sumę modulo 2 z kluczem,
xor - oznacza sumę modulo 2 po wszystkich bitach,
kółko z krzyżykiem - oznacza sumę modulo 2 po wszystkich bitach,
IP - permutacja początkowa,
-IP - permutacja końcowa,
można to przedstawić schematycznie tak:
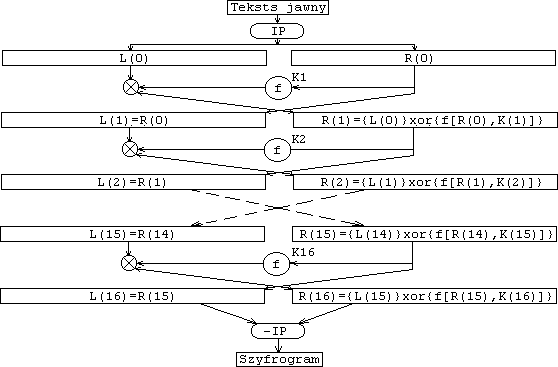
DES pracuje na 64-bitowych blokach. Po początkowej permutacji blok wejściowy dzielony jest na lewą i prawą połowę, każda o długości 32 bitów. Następnie wykonywanych jest 16 cykli jednakowych operacji, nazywanych fynkcjami f, w czasie których dane są łączone z kluczem. Po szesnastym cyklu lewa i prawa połowa są łączone i końcowa permutacja (odwrotna do początkowej) kończy przebieg algorytmu.
W każdym cyklu bity klucza są przesuwane, a następnie jest wybieranych 48 z 56 bitów klucza. Prawa połowa bloku jest rozszerzana do 48 bitów za pomocą permutacji z rozszerzeniem, łączona za pomocą sumy modulo 2 po wszystkich bitach (będę to dla wygody nazywal xorowaniem) z 48 bitami przesuniętego i spermutowanego klucza, jest dokonywanie podstawienie 32 nowych bitów za pomocą algorytmu podstawiania, a potem jeszcze raz dokonywana jest permutacja. Te operacje tworzą funkcję f. Ciąg wyjściowy funkcji f jest dalej łączony z lewą połową za pomocą xorowania. Wynikiem tych operacji jest nowa lewa połowa bloku, stara lewa połowa bloku staje się nową prawą połową. Operacje te są powtarzane 16 razy, tworząc 16 cykli algorytmu DES. Schemat pojedyńczego cyklu wygląda następująco:
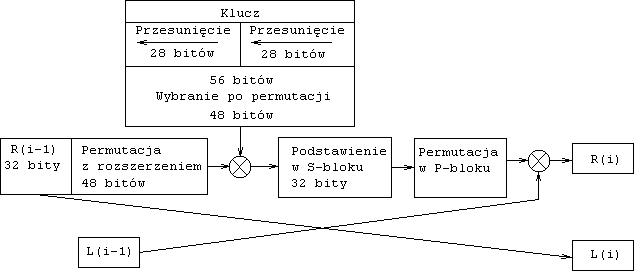
Prześledźmy teraz dokładnie poszczególne fazy algorytmu.
1. Permutacja początkowa.
Permutacja początkowa dokonuje transpozycji (przestawienia poszczególnych bitów) bloku wejściowego, tak, jak to widać w tabeli 1. Tabela ta tak jak inne tu zamieszczone powinna być czytana od prawej do lewej i z gówy na dół. Na przykład permutacja początkowa dokonuje przestawienia bitu 58 na pozycję 1, bitu 50 na pozycję bitu 2, bitu 42 na pozycję bitu 3 itd.
Tabela 1 (permutacja początkowa)Permutacja początkowa i odpowiadająca jej permutacja końcowa nie wpływają na bezpieczeństwo DES. Jej obecność można wytłumaczyć tym, że taka operacja jest banalna do wykonania i niezwykle szybka w hardwarowej wersji (wystarczu pociągnąc odpowiednio "druty"), natomiast jest dość trudna i pracochłonna w softwarowej wersji. Dlatego też wiele implemetacji programowych DES pomija zarówno początkową jak i końcową permutację. Taki algorytm nie jest mniej bezpieczny od standardowego DES, lecz nie jest z nim też w pełni zgodny i nie powinien się nazywać DES.
*****************************************************************************
58 50 42 34 26 18 10 2 60 52 44 36 28 20 12 4
62 54 46 38 30 22 14 6 65 56 48 40 32 24 16 8
57 49 41 33 25 17 9 1 59 51 43 35 27 19 11 3
61 53 45 37 29 21 13 5 63 55 47 39 31 23 15 7
*****************************************************************************
2. Przekształcenia klucza.
Początkowo 64-bitowy klucz DES jest redukowany do 56 bitów przez pominięcie co ósmego bitu (lub wykorzystanie go do kontroli parzystości klucza), jest to opisane w tabeli 2.
Tabela 2 (permutacja klucza)Po wycięciu 56 bitów klucza, za kożdym razem inny 48-bitowy klucz jest generowany dla każdego cyklu DES. Klucze te, K(i), są tworzone w następujący sposób. Najpierw 56 bitów klucza dzieli się na dwie połowy po 28 bitów. Następnie połowy te są przesuwane o jeden lub o dwa bity, zależnie od numeru cyklu. Zależność ta jest pokazana w tabeli 3.
*******************************************************************
57 49 41 33 25 17 9 1 58 50 42 34 26 18
10 2 59 51 43 35 27 19 11 3 60 52 44 36
63 55 47 39 31 23 15 7 62 54 46 38 30 22
14 6 61 53 45 37 29 21 13 5 28 20 12 4
*******************************************************************
Tabela 3 (permutacja klucza w zaleznosci od cyklu)Po wykonaniu przesunięć jest wybieranych 48 z 56 bitów. Ponieważ w operacji tej dokonuje się zmiany porządku występowania bitów jak również wyboru podciągu bitów, zatem nosi ona nazwę permutacji z kompresją lub permutowanego wyboru. Operacja ta dostarcza podciągu bitów o tej samej długości jak ciąg wyjściowy operacji permutowania z rozszerzeniem. Tabela 4 zawiera definicję permutacji z kompresją. Na przykład bit na pozycji 33 przesuniętego klucza jest przesuwany na pozycję 35 ciągu wyjściowego, a bit na pozycji 18 przesuniętego klucza jest pomijany.
*************************************************************************
Cykl: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Liczba przesunięć: 1 1 1 2 2 2 2 2 1 2 2 2 2 2 2 1
*************************************************************************
Tabela 4 (permutacja kompresji)3. Permutacja z rozszerzeniem.
*********************************************************
14 17 11 24 1 5 3 28 15 6 21 10
23 19 12 4 26 8 16 7 27 20 13 2
41 52 31 37 47 55 30 40 51 45 33 48
44 49 39 56 34 53 46 42 50 36 29 32
*********************************************************
W permutacji tej prawa połowa danych R(i), jest rozszerzana z 32 do 48 bitów. Ponieważ operacja ta zmienia kolejność bitów, a niektóre bity są powtarzane, więc jest znana jako permutacja z rozszerzeniem. Operacja ta ma dwa cele: dostarczenie ciągu o tej samej długości co xorowany z nim ciąg klucza i ciągu wydłużonego, który może być poddany kompresji przy operacji podstawiania. Jednak żaden z tych celów nie jest jej głównym celem kryptograficznym. Pozwalając jednemu bitowi wpływać na dwa podstawienia, uzyskujemy to, że zależność bitów wyjściowych od bitów wyjściowych szybciej się rozprzestrzeniała. Innymi słowy chodzi o to, by dwa szyfrogramy tekstów, różniących się tylko jednym bitem różniły się od siebie dość znacznie. Jest to nazywane efektem lawinowym. Wiele elementów projektu DES obraca się wokół tego, by jak najszybciej osiągnąć stan, w którym każdy bit szyfrogramu zależy od każdego bitu tekstu jawnego i każdego bitu klucza. Tabela 5 przedstawia jak zbudowana jest permutacja z rozszerzeniem.
Tabela 5 (permutacja z rozszerzeniem)Chociarz blok wyjściowy jest dłuższy od bloku wejściowego, to jest tylko jeden blok wejściowy, który może wygenerować określony blok wyjściowy.
*********************************************************
32 1 2 3 4 5 4 5 6 7 8 9
8 9 10 11 12 13 12 13 14 15 16 17
16 17 18 19 20 21 20 21 22 23 24 25
24 25 26 27 28 29 28 29 30 31 32 1
*********************************************************
4. Podstawienia realizowane w S-blokach
Po zxorowaniu skompresowanego klucza z rozszerzonym blokieb 48-bitowym wynik jest poddawany operacji podstawiania. Podstawiania są dokonywane przez osiem bloków podstawień, zwanych S-blokami (ang. Substitution boxes). Ciąg o długości 48 bitów jest dzielony na osiem bloków 6-bitowych.Każdy oddzielny blok ciągu bitów jest przetwarzany przez oddzielny S-blok: blok 1 jest przetwarzany przez S-blok 1, blok 2 przez S-blok 2 itd. Każdy S-blok jest opisany w postaci tabeli złożonej z 4 wierszy i 16 kolumn. Każdy element tej tabeli jest 4 bitową liczbą. Sześć bitów wejściowych S-bloku określa, w którym wierszu i w której kolumnie należy szukać ciągu wyjściowego. Tabele 6-13 zawierają struktury wszystkich S-bloków.
Tabela 6 (S-blok 1)
*****************************************************************************
14 4 13 1 2 15 11 8 3 10 6 12 5 9 0 7
0 15 7 4 14 2 13 1 10 6 12 11 9 5 3 8
4 1 14 8 13 6 2 11 15 12 9 7 3 10 5 0
15 12 8 2 4 9 1 7 5 11 3 14 10 0 6 13
*****************************************************************************
Tabela 7 (S-blok 2)
*****************************************************************************
15 1 8 14 6 11 3 4 9 7 2 13 12 0 5 10
3 13 4 7 15 2 8 14 12 0 1 10 6 9 11 5
0 14 7 11 10 4 13 1 5 7 12 6 9 3 2 15
13 8 10 1 3 15 4 2 11 6 7 12 0 5 14 9
*****************************************************************************
Tabela 8 (S-blok 3)
*****************************************************************************
10 0 9 14 6 3 15 5 1 13 12 7 11 4 2 8
13 7 0 9 3 4 6 10 2 8 5 14 12 11 15 1
13 6 4 9 8 15 3 0 11 1 2 12 5 10 14 7
1 10 13 0 6 9 8 7 4 15 14 3 11 5 2 12
*****************************************************************************
Tabela 9 (S-blok 4)
*****************************************************************************
7 13 14 3 0 6 9 10 1 2 8 5 11 12 4 15
13 8 11 5 6 15 0 3 4 7 2 12 1 10 14 9
10 6 9 0 12 11 7 13 15 1 3 14 5 2 8 4
3 15 0 6 10 1 13 8 9 4 5 11 12 7 2 14
*****************************************************************************
Tabela 10 (S-blok 5)
*****************************************************************************
2 12 4 1 7 10 11 6 8 5 3 15 13 0 14 9
14 11 2 12 4 7 13 1 5 0 15 10 3 9 8 6
4 2 1 11 10 13 7 8 15 9 12 5 6 3 0 14
11 8 12 7 1 14 2 13 6 15 0 9 10 4 5 3
*****************************************************************************
Tabela 11 (S-blok 6)
*****************************************************************************
12 1 10 15 9 2 6 8 0 13 3 4 14 7 5 11
10 15 4 2 7 12 9 5 6 1 13 14 0 11 3 8
9 14 15 5 2 8 12 3 7 0 4 10 1 13 11 6
4 3 2 12 9 5 15 10 11 14 1 7 6 0 8 13
*****************************************************************************
Tabela 12 (S-blok 7)
*****************************************************************************
4 11 2 14 15 0 8 13 3 12 9 7 5 10 6 1
13 0 11 7 4 9 1 10 14 3 5 12 2 15 8 6
1 4 11 13 12 3 7 14 10 15 6 8 0 5 9 2
6 11 13 8 1 4 10 7 9 5 0 15 14 2 3 12
*****************************************************************************
Tabela 13 (S-blok 8)Bity wejściowe określają element tabeli opisującej S-blok w bardzo szczególny sposób. Rozważmy sześć bitów wejściowych S-bloku, które oznaczmy kolejno b1, b2, b3, b4, b5 i b6. Bity b1 i b6 łączy się, tworząc liczbę 2-bitową, przyjmującą wartości od 0 do 3, która określa numer wiersza w tabeli. Środkowe cztery bity od b2 do b5 łączy się, aby utworzyć liczbę 4-bitową, która przyjmuje wartości od 0 do 15, która określa numer kolumny w tabeli. Załóżmy na przykład, że ciąg wejściowy do szóstego S-bloku (tzn. bity na pozycjach od 31 do 36 ciągu będącego wynikiem zorowania w poprzednich krokach) jest równy 110010. Pierwszy i ostatni bit tego ciągu tworzą liczbę 10, która określa 2 wiersz w tabeli szóstego S-bloku. środkowe bity tworzą liczbę 1001, która wyznacza dziewiątą kolumnę w tej samej tabeli (szóstego S-bloku). Elementem leżącym w drugim wierszu i dziewiątej kolumnie jest 0 (pamiętajmy o numerowaniu wierszy i kolumn od 0, nie zaś od 1). Zatem za ciąg 110010 podstawiany jest ciąg 0000. Opisany wyżej proces jest krytycznym etapem całego algorytmu. Wszystkie inne operacje są liniowe i łatwe do analizy. S-bloki realizują operacje nielinowe i bardziej niż cokolwiek innego zapewniają bezpieczeństwo dawane przez DES. Wynikiem tej fazy jest 8 4-bitowych bloków, które łącznie tworzą pojedynczy blok 32-bitowy. Blok ten jest przesuwany do następnego etapu: permutacji w P-bloku.
*****************************************************************************
13 2 8 4 6 15 11 1 10 9 3 14 5 0 12 7
1 15 13 8 10 3 7 4 12 5 6 11 0 14 9 2
7 11 4 1 9 12 14 2 0 6 10 13 15 3 5 8
2 1 14 7 4 10 8 13 15 12 9 0 3 5 6 11
*****************************************************************************
5. Permutacja w P-bloku.
Jest to zwyczajna permutacja. Żadne bity nie są kopiowane, ani żadne nie są pomijane, tylko są pomiędzy sobą zamieniane miejscami. Dlatego też ten etap nazywamy permutacją zwykłą, lub po prostu permutacją. Poniższa tabela 14 pokazuje schemat tej permutacji.
Tabela 14 (permutacja P-bloku)Na zakończenie tego etapu wynik permutacji w P-bloku jest xorowany z lewą połową początkowego bloku 64-bitowego. Następnie lewa i prawa połowa są zamieniane miejscami i zaczyna się kolejny cykl.
*****************************************************************************
16 7 20 21 29 12 28 17 1 15 23 26 5 18 31 10
2 8 24 14 32 27 3 9 19 13 30 6 22 11 4 25
*****************************************************************************
6. Permutacja końcowa.
Ta permutacja jest odwrotnością permutacji początkowej. Nie będę więc zamieszczał tu tabeli, która to opisuje. Wystarczy skonstruować permutację odwrotną do permutacji początkowej. Należy jeszcze tylko pamiętać, żeby po zakończeniu ostatniego cyklu algorytmu DES nie są zamieniane miejscami połowy prawa z lewą. Należy to więc teraz zrobić i dopiero wtedy zaaplikować permutację końcową. Zauważmy, że zamiana lewej połowy danych z prawą jest tez permutacją. W związku z tym można złożyć te dwie permutacje i na zakończenie wykonywać tylko jedną. Tak jest to rozwiązane w implementacjach softwarowych, ze względu na szybkość. Jeśli chopdzi o hardware, to tam permutacja, to są zwyczajne druty, więc nawet się nie zauważa, że są dwie permutacje zamiast jednej, należy jednak wiedzieć, że coś takiego istnieje (tzn. końcowa permutacja nie jest odwrotnością permutacji początkowej, tylko złożeniem odwrotności permutacji początkowej z permutacją zamieniającą lewą połowę danych z prawą).
Tak wygląda szyfrowanie algorytmem DES. Po przeczytaniu tego i chwili namysłu może nasunąć Ci się pytanie. No dobra, szyfrowanie jest dość skomplikowane i wydaje się, że daje na wyjściu dane, które nie zdradzają żadnego powiazania z danymi wejściowymi. Ale jak to wtedy odszyfrować? Logiczne wydawałoby się, że należałoby całe szyfrowanie wykonać w odwrotnej kolejności, to jest od końca do początku. Ale dla S-bloków to jest niemożliwe! Jednemu wynikowi otrzymanemu przez S-blok, odpowiada wiele potencjalnych danych wejściowych. Pomaga tu jednak następujący trik. Zauważmy, że dla i-tego cyklu w algorytmie DES zachodzą następujące związki:
L(i+1)=R(i)
R(i+1)=L(i)xorf(R(i),K(i+1))
przyjmując oznaczenia, takie jak wcześniej (na górze tego tekstu). Z tego wynika, że:
R(i-1)=L(i)
L(i-1)=R(i)xorf(R(i-1),K(i))=R(i)xorf(L(i),K(i))
Jeśli więc mamy L(i), R(i) oraz podklucz K(i), to na podstawie powyższych równości możemy obliczyć L(i-1) i R(i-1). Tak więc nie musimy wcale obliczać funkcji odwrotnych do funkcji S-bloków. Łatwo widać, że podczas deszyfrowania wykonywane są te same operacje, co podczas szyfrowania (tylko podklucze występują w odwrotnej kolejności). Z tego powodu ten sam hardware może być używane do szyfrowania jak i deszyfrowania (a co za tym idzie DES jest bardzo przyjemnym hardwarowo algorytmem).
Myślę, że taki opis algorytmu DES może się przydać komuś, kto zamierza napisać swój program do szyfrowania i wykorzystać w nim DES. Może to też zainteresować kogoś, kto po prostu chce wiedzieć na czym opierają się obecne szyfry. Zauważmy, że istota algorytmu DES opiera się na zastosowaniu dwóch podstawowych technik w szyfrach symetrycznych: podstawianiu (S-bloki) i przestawianiu (wszechobecne permutacje). Jaki poziom bezpieczeństwa daje DES? Gdzie jest używany? Jak zabierano się do jego łamania i jakie wyniki uzyskano? Jak ulepszyć DES, tak, by był o wiele bardziej bezpieczny? Jak zaszyfrować algorytmem DES dowolnie długie teksty (zauważmy, że DES jest w zasadzie przeznaczony do szyfrowania tylko 64 bitów danych!)? O tym napiszę w następnym odcinku. Wiec, do następnego razu...
by YAHRO (yahro@go2.pl) na podstawie:
"Kryptografia dla praktyków", autor: Bruce Schneier,
"Kryptografia", autor: Mirosław Kutyłowski, Willy-B. Strothmann,
"Algebraiczne aspekty kryptografii", autor: Neal Koblitz.
Autor: Paweł Kopczyński
