Funkcje trygonometryczne
Funkcje trygonometryczne kąta ostrego
Funkcje trygonometryczne są głównymi pojęciami trygonometrii. Istnieje sześć funkcji trygonometrycznych:
- sinus (czyt. sinus), symbol: sin
- cosinus (czyt. kosinus), symbol: cos
- tangens (czyt. tangens), symbol: tg, tan
- cotangens (czyt. kotangens), symbol: ctg, cot, ctn
- secans (czyt. sekans), symbol: sec,
- cosecans (czyt. kosekans), symbol: cosec, csc
Argumentami funkcji trygonometrycznych mogą być:
- kąt skierowany
- liczba rzeczywista
| DEFINICJA funkcji trygonometrycznych dla kąta ostrego w trójkącie prostokątnym. Sinusem kąta ostrego α nazywamy stosunek przyprostokątnej leżącej na przeciw kąta α do przeciwprostokątnej
Cosinusem kąta ostrego α nazywamy stosunek przyprostokątnej leżącej przy kącie α do przeciwprostokątnej
Tangensem kąta ostrego α nazywamy stosunek przyprostokątnej leżącej na przeciw kąta α do przyprostokątnej leżącej przy kącie α
Cotangensem kąta ostrego α nazywamy stosunek przyprostokątnej leżącej przy kącie α do przyprostokątnej leżącej na przeciw kąta α 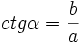 lub lub 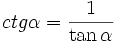 Secansem kąta ostrego α nazywamy stosunek przeciwprostokątnej do przyprostokątnej leżącej przy kącie α 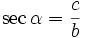 lub lub 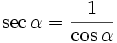 Cosecansem kąta ostrego α nazywamy stosunek przeciwprostokątnej do przyprostokątnej leżącej na przeciw kąta α 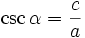 lub lub 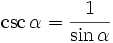 |
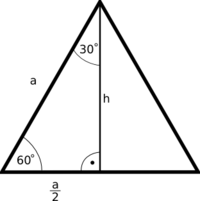
Wyznaczanie wartości funkcji trygonometrycznych dla kątów 30°, 45° i 60°
Wyznaczyć wartości funkcji tryg. dla kątów o mierze 30° i 60° można za pomocą trójkąta równobocznego, wykorzystując do tego jego własności.
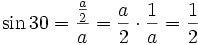
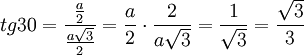
A teraz korzystając z własności kwadratu obliczymy wartości funkcji trygonometrycznej dla kąta o mierze 45°.
Z powyższych wyliczeń można stworzyć tabelkę, której będziesz musiał nauczyć się na pamięć.
| × | 30° | 45° | 60° |
|---|---|---|---|
| sin |  | ||
| cos |  | ||
| tg | 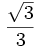 | 1 | 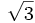 |
| ctg | 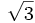 | 1 | 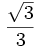 |
Miara łukowa kąta
Narysujmy okrąg o promieniu r, a na nim zaznaczmy łuk L, dla którego kąt środkowy oparty o ten łuk będzie wynosił 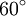 . Znajdźmy wzór na długość tego łuku.
. Znajdźmy wzór na długość tego łuku.
Intuicyjnie długość łuku do obwodu okręgu jest równa mierze kąta w stopniach do 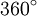 :
:
ponieważ Ob = 2πr, otrzymujemy:
zatem:
Jak łatwo zauważyć wartość 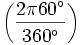 nie zależy od promienia naszego okręgu, tylko od kąta, który tworzy nasz łuk. Wartość ta nazywana jest miarą łukową kąta dla kąta
nie zależy od promienia naszego okręgu, tylko od kąta, który tworzy nasz łuk. Wartość ta nazywana jest miarą łukową kąta dla kąta 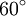 . W ogólności wzór na długość łuku wyznaczonego przez kąt
. W ogólności wzór na długość łuku wyznaczonego przez kąt 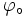 (wyznaczonego w stopniach) przybierze postać:
(wyznaczonego w stopniach) przybierze postać:
Tak jak długość nie musi wyrażać się w metrach, tak też kąt nie musi wyrażać się w stopniach. Możemy wykorzystać inną jednostkę kąta, jakim jest radian. Wtedy wartość kąta jest wyrażana w tzw. mierze łukowej. Załóżmy, że kąt 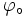 jest wyrażony w stopniach,
jest wyrażony w stopniach, 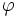 w radianach, wówczas wartości tych kątów wiąże zależność:
w radianach, wówczas wartości tych kątów wiąże zależność:
Jednostką miary łukowej jest radian, który w skrócie zapisywany jest przez rad. Często przy podawaniu kąta wyrażonego w mierze łukowej pomija się jednostkę np. zamiast 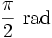 pisze się po prostu
pisze się po prostu  .
.
Powróćmy znowu do wzoru na długość łuku l, jednak tym razem jednak załóżmy, że kąt na którym jest oparty łuk jest wyrażony w radianach i wynosi α. Wówczas wykorzystując zależność 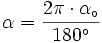 otrzymujemy zależność:
otrzymujemy zależność:
dzieląc obustronnie przez r otrzymujemy:
| DEFINICJA Miarą łukową kąta nazywamy stosunek długości łuku do długości promienia. Jest ona równa kątowi α, który wyznacza ten łuk: Jednostką miary łukowej jest radian. |
Ten drugi wzór jest o wiele łatwiejszy do zapamiętania.
Zauważmy, że miara kąta pełnego wyrażonego w stopniach wynosi 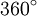 , a w radianach
, a w radianach 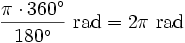 . Zatem:
. Zatem:
Aby zamienić stopnie na radiany możemy wykorzystać wcześniej wzór:
(który był przedstawiony wcześniej, lecz w nieco innej postaci).
Odwrotnie, aby zamienić radiany na stopnie wykorzystujemy wzór:
Możemy go o trzymać przekształcając poprzedni wzór.
Przykład 1 Zamieńmy miarę stopniową na miarę łukową
- a)
- b)
- c)
Wówczas możemy to zrobić na dwa sposoby:
- a) I sposób za pomocą proporcji:
- 2π -
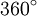
- x -
- 2π -
- czyli:
- II sposób, wykorzystując wzór:
- b)
- c)
Przykład 2 Zamieńmy miarę łukową na miarę stopniową
- a)
- b)
- b)
Podobnie jak w poprzednim przykładzie, możemy to zrobić na dwa sposoby:
- a) I sposób za pomocą proporcji:
- 2π -
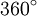
- - x
- 2π -
- zatem:
- II sposób, wykorzystując wzór:
- b)
- c)
Funkcje trygonometryczne kąta dowolnego
Miara kąta skierowanego na płaszczyźnie zorientowanej
| DEFINICJA Kąt skierowany - jest to uporządkowana para półprostych o wspólnym początku; pierwsza półprosta - ramię początkowe, druga półprosta - ramię końcowe. |
Przykład kąta skierowanego
Ramieniem początkowym kąta α jest półprosta wyróżniona na niebiesko, a ramieniem końcowym półprosta koloru czerwonego.
| DEFINICJA Płaszczyzna zorientowana - jest to taka płaszczyzna na której określono bieg dodatni dla każdego okręgu. |
| Przykład płaszczyzna zorientowana 1: Układ współrzędnych zorientowany dodatnio. | Przykład płaszczyzna zorientowana 2: Układ współrzędnych zorientowany ujemnie. |
Kątowi skierowanemu na płaszczyźnie zorientowanej przyporządkowujemy ten kąt nieskierowany AOB (wypukły lub wklęsły) w którym leży łuk o początku w punkcie L i końcu w punkcie K, mający zwrot dodatni.
Funkcje trygonometryczne kąta skierowanego
| DEFINICJA {{{1}}} |
Przykład 1.
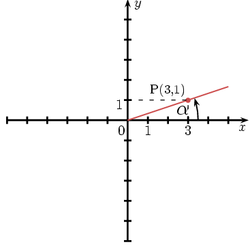
Niech ramię początkowe kąta α pokrywa się z dodatnią półosią OX, a ramię końcowe przechodzi przez punkt P(3,1). Wyznaczmy wartości funkcji sinus, cosinus, tangens i cotangens dla tego kąta. Ponieważ wartości funkcji trygonometrycznych nie zależą od wyboru punktu należącego do końcowego ramienia kąta, zatem możemy wykorzystać do tego współrzędne punktu P(3,1):
Mówimy, że kąt jest w położeniu standardowym, jeśli kąt został umieszczony tak w układzie współrzędnych, że jego ramię początkowe pokrywa się z dodatnią osią OX.
Przykład 2.
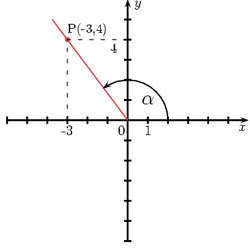
Kąt α znajduje się w położeniu standardowym. Końcowe ramię przechodzi przez punkt P( − 3,4). Wyznaczmy sinα, cosα, tgα, ctgα.
Przykład 3.
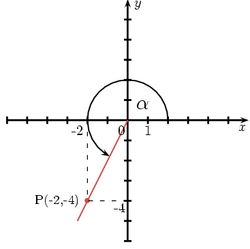
Kąt α znajduje się w położeniu standardowym. Końcowe ramię przechodzi przez punkt P( − 2, − 4). Obliczmy sinα, cosα, tgα, ctgα.
Własności funkcji trygonometrycznych
Znak funkcji trygonometrycznej
| Funkcja | I | II | III | IV |
|---|---|---|---|---|
| sinα | + | + | - | - |
| cosα | + | - | - | + |
| tgα | + | - | + | - |
| ctgα | + | - | + | - |
| Czy wiesz, że... Powyższe znaki funkcji trygonometrycznych można nauczyć się stosując prosty wierszyk: "W pierwszej wszystkie są dodatnie, w drugiej tylko sinus, w trzeciej tangens i cotangens, a w czwartej cosinus". |
Parzystość i nieparzystość
Funkcja cosα jest parzysta, czyli zachodzi:
- cosα = cos( − α)
Natomiast funkcje sinα, tgα i ctgα są nieparzyste, czyli:
- sinα = − sin( − α)
- tgα = − tg( − α)
- ctgα = − ctg( − α)
Okresowość
Dla funkcji trygonometryczny sinα, cosα, tgα, ctgα, gdzie α jest dowolnym kątem, a k dowolną liczbą całkowitą, zachodzi:
Związki pomiędzy funkcjami trygonometrycznymi
- sin2x + cos2x = 1
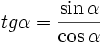
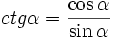
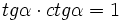
Wykresy funkcji trygonometrycznych
Wykres funkcji sinus nazywa się sinusoidą, funkcji cosinus cosinusoidą, funkcji tangens tangensoidą, a funkcji cotangens cotangensoidą.
Na podstawie wykresu poszczególnych funkcji trygonometrycznych można oszacować cechy tej funkcji:
Sinusoida
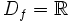
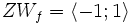
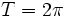
- f(x) = 0 dla
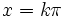 gdzie
gdzie 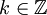
- nieparzystość
- okresowość
Cosinusoida
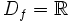
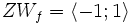
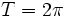
- f(x) = 0 dla
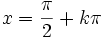 gdzie
gdzie 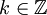
- parzystość
- okresowość
Tangensoida
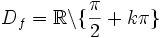 gdzie
gdzie 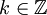
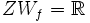
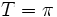
- f(x) = 0 dla x = kπ gdzie
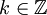
- asymptoty pionowe
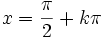 gdzie
gdzie 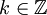
- nieparzystość
- okresowość
Cotangensoida
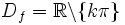 gdzie
gdzie 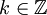
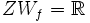
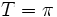
- f(x) = 0 dla
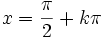 gdzie
gdzie 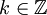
- asymptoty pionowe x = kπ gdzie
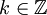
- nieparzystość
- okresowość
Szkicowanie wykresu funkcji trygonometrycznych
Szkicowanie zaczynamy od narysowania układu współrzędnych i zaznaczenia na osi OY wartości:
- w przypadku sinusa i cosinusa: od -1 do 1,
- w przypadku tagensa i cotangensa od -4 do 4.
Natomiast na osi OX wartości od − π do 3π. Zakładam, że będziesz rysował wykres na kartce w kratkę, więc zalecam byś przyjął jako jednostkę na osi Y 2 kratki. Wykonując podziałkę na osi X nanieś ją w następujący sposób:
- większymi kreskami co kratkę, będą to wartości rosnące co
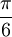
- mniejszymi kreskami co półtorej kratki, będą to wartości rosnące co
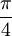
Gdy mamy tak przygotowany wykres możemy przystąpić to nanoszenia punktów przez które wiemy, że funkcja będzie na pewno przechodziła (z tabeli), a następnie korzystając z wzorów redukcyjnych możemy je zaznaczyć dla dowolnego kąta.
Tak zaznaczone punkty łączymy płynną linią i gotowe.
!!! Uwaga !!! W przypadku kreślenia wykresu funkcji tangens i cotangens należy zaznaczyć asymptotę linią przerywaną.
Tożsamości trygonometryczne
Podstawowe tożsamości trygonometryczne
sin2α + cos2α = 1
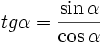
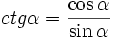
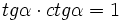
Dowód prawdziwości sin2α + cos2α = 1:
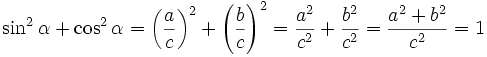
Na podstawie twierdzenia Pitagorasa możemy stwierdzić, że 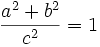 ponieważ
ponieważ
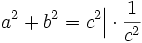
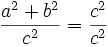
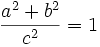
Dowód prawdziwości 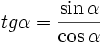
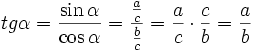
Dowód prawdziwości 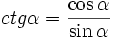
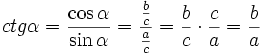
Dowód prawdziwości 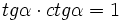
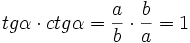
Pozostałe tożsamości trygonometryczne
Funkcje sumy i różnicy kątów
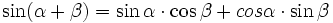
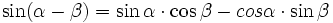
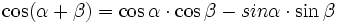
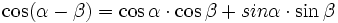
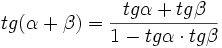 , jeżeli
, jeżeli 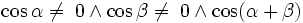
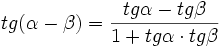 , jeżeli
, jeżeli 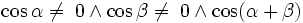
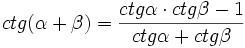 , jeżeli
, jeżeli 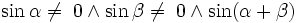
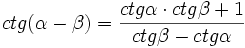 , jeżeli
, jeżeli 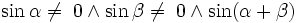
sumy i różnice funkcji trygonometrycznych
Dla dowolnych kątów o miarach α i β
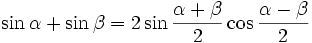
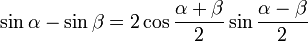
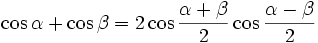
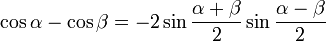
funkcje kąta podwójnego
sin2α = 2sinαcosα
cos2α = cos2α − sin2α
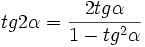 , jeżeli
, jeżeli 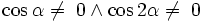
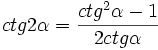 , jeżeli
, jeżeli 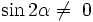
Wzory redukcyjne
Wzory redukcyjne – wzory pozwalające sprowadzić obliczanie wartości funkcji trygonometrycznych dowolnego kąta skierowanego do obliczenia wartości funkcji dla kąta ostrego.
| sin( − α) = − sin(α) cos( − α) = cos(α) tg( − α) = − tg(α) ctg( − α) = − ctg(α) | sin(90 − α) = cos(α) cos(90 − α) = sin(α) tg(90 − α) = ctg(α) ctg(90 − α) = tg(α) | sin(90 + α) = cos(α) cos(90 + α) = − sin(α) tg(90 + α) = − ctg(α) ctg(90 + α) = − tg(α) |
| sin(180 − α) = sin(α) cos(180 − α) = − cos(α) tg(180 − α) = − tg(α) ctg(180 − α) = − ctg(α) | sin(180 + α) = − sin(α) cos(180 + α) = − cos(α) tg(180 + α) = tg(α) ctg(180 + α) = ctg(α) | sin(270 − α) = − cos(α) cos(270 − α) = − sin(α) tg(270 − α) = ctg(α) ctg(270 − α) = tg(α) |
| sin(270 + α) = − cos(α) cos(270 + α) = sin(α) tg(270 + α) = − ctg(α) ctg(270 + α) = − tg(α) | sin(360 − α) = − sin(α) cos(360 − α) = cos(α) tg(360 − α) = − tg(α) ctg(360 − α) = − ctg(α) |
Na całe szczęście nie trzeba uczyć się powyższej gigantycznej tabeli na pamięć. Wystarczy zapamiętać dwa zdroworozsądkowe fakty wynikających z niej:
- gdy we wzorze redukcyjnym występuje liczba 90 lub 270 to funkcja sinus zmienia się cosinus i na odwrót, a tangens na cotangens i na odwrót
- o pojawieniu się znaku minus decyduje funkcja po lewej stronie gdy w danej ćwiartce dana funkcja jest ujemna to do dopisujemy znak minus np.:
cos(270 + α) = sin(α) – ponieważ cosinus w IV ćwiartce (270 + α) jest dodatni
cos(90 + α) = − sin(α) – ponieważ cosinus w II ćwiartce (90 + α) jest ujemny
tg(180 − α) = − tg(α) – ponieważ tangens w II ćwiartce (180 − α) jest ujemny
Łatwo zapamiętać gdzie pojawia się znak minus używając "praktycznej poezji matematycznej":
W pierwszej ćwiartce wszystkie funkcje są dodatnie
W drugiej tylko sinus
W trzeciej tangens i cotangens
A w czwartej cosinus
Równania trygonometryczne
Równaniem trygonometrycznym będziemy nazywać równanie, w którym niewiadoma występuje tylko w wyrażeniach będących argumentem funkcji trygonometrycznej. Przykładami równań trygonometrycznych mogą być:
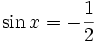
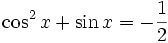
- tgx = 100
| TWIERDZENIE Równanie postaci sinx = a ma nieskończenie wiele rozwiązań, przy założeniu, że
|
Przykład 1. Rozwiążmy równanie 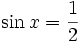 :
:
- Ponieważ
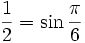 , więc
, więc 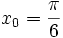
- Stąd mamy:
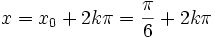
- lub
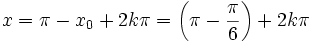 , gdzie
, gdzie 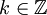
Odp. Rozwiązaniem równania są liczby postaci: 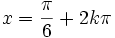 lub
lub 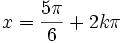 ,
, 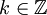 .
.
Przykład 2. Rozwiążmy równanie 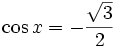 :
:
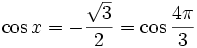
- Zatem:
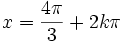 lub
lub 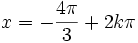 , gdzie
, gdzie 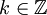
Odp. Rozwiązaniem równania są liczby postaci: 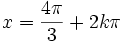 lub
lub 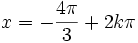 ,
, 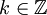 .
.
Przykład 3. Rozwiążmy równanie tgx = − 1:
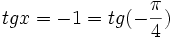
- Zatem:
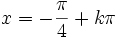 , gdzie
, gdzie 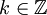
Odp. Rozwiązaniem równania są liczby postaci: 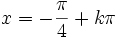 ,
, 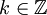 .
.
Nierówności trygonometryczne
Przykładami nierówności trygonometrycznych mogą być:
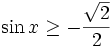
- sin2x − cosx + 2 < 0
- tgx + ctgx > 1
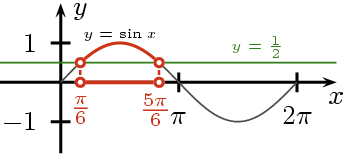
Przykład 1. Rozwiążmy graficznie nierówność: 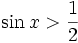 w przedziale [0;2π].
w przedziale [0;2π].
Z wykresu możemy odczytać, że sinus przyjmuje wartości większe od  dla
dla ![x \in \left[\frac{\pi}{6};\frac{5\pi}{6}\right]](https://jpcdn.it/img/9dcaff273e26c5b997e4a2debcd1704d.png) .
.
Odp. Nieróność 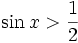 w przedziale [0;2π] jest spełniona dla
w przedziale [0;2π] jest spełniona dla ![x \in \left[\frac{\pi}{6};\frac{5\pi}{6}\right]](https://jpcdn.it/img/9dcaff273e26c5b997e4a2debcd1704d.png) .
.
Autor: Wikibooks

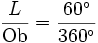
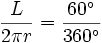
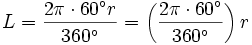
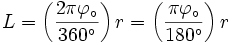
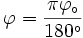
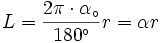
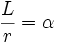
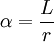
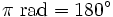
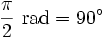
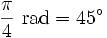
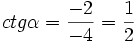
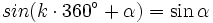
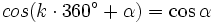
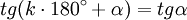
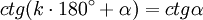
![a \in [-1;1]](https://jpcdn.it/img/81cdd5a900393508a270e9cb5d406a40.png) :
: