Zbiory (matematyka)

Zbiór jest jednym z podstawowych pojęć matematycznych. Pojęcia tego nie definiujemy - jest ono pojęciem pierwotnym. Czasami zamiast „zbiór" powiemy "rodzina", rzadziej "przestrzeń". W dalszym ciągu będziemy wykorzystywać intuicyjne rozumienie zbioru jako pewnej całości złożonej z wielu przedmiotów, które będziemy nazywać elementami tego zbioru.

Zobaczmy na przykłady:

zbiór ciastek
zbiór książek
zbiór liczb całkowitych nieparzystych
zbiór uczniów w klasie

Wyobraźmy sobie, że trzymamy w ręce cztery cukierki - jeden o smaku cytrynowym, drugi o smaku truskawkowym, trzeci o smaku jabłkowym a czwarty o smaku waniliowym. Zbiory są oznaczane zazwyczaj dużymi literami alfabetu np. A, B, C, D, więc możemy nasz zbiór cukierków nazwać literą C, jak łatwo się domyśleć od nazwy „cukierki".

Jeśli coś, jakiś przedmiot należy do pewnego zbioru, najczęściej oznacza się go małą literą np. x, y, z, dlatego też oznaczmy cukierek cytrynowy jako c, truskawkowy jako t, jabłkowy jako j, a waniliowy jako w.

Jeśli element a należy do zbioru A, zapisujemy to 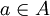$a \in A$ i czytamy „a należy do zbioru A". Możemy zapisać używając naszych oznaczeń, że cukierek truskawkowy t należy do naszego zbioru cukierków C jako 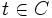$t \in C$ . Podobnie, aby zaznaczyć, że dany element nie należy do danego zbioru, używamy znaku 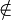$\notin$ , czyli jeśli a nie należy do zbioru A zapiszemy 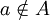$a \notin A$ . 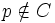Ponieważ nie posiadamy cukierka pomarańczowego p, cukierek p nie należy do naszego zbioru cukierków C, a to zapiszemy jako $p \notin C$ .

Często element należący do danego zbioru jest oznaczany taką samą literą co zbiór, lecz z małej litery np. element zbioru X nieraz jest oznaczany przez x, a element zbioru A jako a. Wymieniane elementy zbioru powinniśmy umieszczać w nawiasach klamrowych. Nasz zbiór C składa się z cukierka cytrynowego c, truskawkowego t, jabłkowego j i waniliowego w, więc możemy zapisać 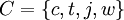$C=\{c,t,j,w\}\$ .

Liczbę elementów zbioru A oznaczamy 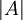$|A|\$ i nazywamy mocą zbioru A. W przykładzie z cukierkami powiemy, że moc zbioru cukierków C wynosi 4 i napiszemy $|C| = 4\$ .

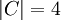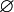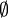Ze względu na liczbę elementów w zbiorze wyróżniamy zbiory skończone np. nasz zbiór cukierków i zbiory nieskończone np. zbiór liczb rzeczywistych. Szczególnym przypadkiem zbioru skończonego jest zbiór pusty, który nie zawiera żadnych elementów. Zbiór pusty oznaczamy zazwyczaj symbolem $\varnothing$ lub $\emptyset$ .

Wielu własności zbiorów domyślamy się intuicyjnie, powinieneś je także znać z poprzednich lat nauki. Więcej o zbiorach powiemy w rozdziale Liczby i ich zbiory.

Zbiory liczb

Wśród nieskończenie wielu zbiorów wyróżniamy pewne zbiory liczb, które odgrywają, jak zresztą same liczby, istotną rolę w matematyce. Do najważniejszych zaliczamy:

zbiór liczb naturalnych
zbiór liczb całkowitych
zbiór liczb wymiernych
zbiór liczb niewymiernych
zbiór liczb rzeczywistych

Przyjrzymy się teraz każdemu pokrótce.

Zbiór liczb naturalnych

Zbiór liczb naturalnych to zbiór wszystkich liczb naturalnych. Z kolei liczba naturalna to liczba, do której możemy doliczyć, wliczając w to zero i te „dużo" większe liczby. Kiedyś może bawiliśmy się w chowanego, wówczas mogliśmy liczyć np. do 25, 50 czy też 100. Wszystko to są liczby naturalne. Liczbą naturalną jest także 4, 1000 i 100000000000. Liczbą naturalną nie będzie natomiast -5, 2,5, π, bo jak mamy policzyć do -5 (no, chyba, że byśmy oszukali i liczyli od -10), czy też 2,5 i do π=3.14...? W jaki sposób najprościej sprawdzić, czy liczba jest naturalna? Zapamiętajmy, że liczba jest naturalna, jeśli nie posiada dodatkowych „udziwnień" typu minusy, czy też przecinki.

W matematyce zbiór liczb naturalnych jest z reguły oznaczany przez 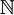$\mathbb{N}$ . Ponieważ początkowe liczby naturalne to 0, 1, 2, 3 itd., więc zbiór liczb naturalnych będzie równy

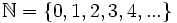$\mathbb{N} = \{0, 1, 2, 3, 4, ...\}$ .

Zbiór liczb całkowitych

Co to znaczy, że liczba jest całkowita? Najprościej powiedzieć, że jest to taka liczba, które nie ma przecinka. Zatem widzimy, że mogą być ujemne. Kilka przykładów to -1, -5, 1000. Liczbą całkowitą znowu nie będzie π. Dlaczego? Bo pamiętamy, że π = 3,14..., a taka liczba ma przecinek. Natomiast liczba 4,0 także jest całkowita, ponieważ po uproszczeniu będzie równa 4, a ta jest całkowita. Podobnie zresztą będzie dla liczb naturalnych.

Zbiór liczb całkowitych będziemy oznaczać przez 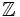$\mathbb{Z}$ . Czyli widzimy, że

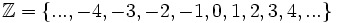$\mathbb{Z} = \{..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ...\}$ .

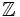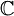A teraz mała dygresja dla bardziej spostrzegawczych. Niektórzy może zarzucą dlaczego $\mathbb{Z}$ a nie $\mathbb{C}$ . To prawda, że w wielu podręcznikach szkolnych używa się literki C do oznaczania zbioru liczb całkowitych, jednak w większości podręczników dotyczących matematyki (nie wierzysz? sam sprawdź) korzysta się z oznaczeń podanych wyżej (czyli litery Z). Poza tym po co masz się uczyć oznaczeń, które i tak będziesz musiał najprawdopodobniej zmienić, gdy pójdziesz na studia? Z podobnych względów oznaczymy zbiór liczb wymiernych literką Q.

Zbiór liczb wymiernych

Liczba wymierna to taka liczba, którą można zapisać w postaci ułamka zwykłego, gdzie licznik i mianownik będzie liczbą całkowitą. Liczbą wymierną będzie liczba 1, 2, 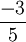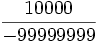$\frac{-3}{5}$ , $\frac{10000}{-99999999}$ , czy też 2,7563. I znowu tu nie wstawimy liczby π, ponieważ nawet gdybyśmy chcieli, to i tak nie bylibyśmy w stanie jej zapisać za pomocą ułamka zwykłego.

Zbiór liczb wymiernych w matematyce oznaczamy przez 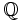$\mathbb{Q}$ .

Zbiór liczb niewymiernych

Analogicznie do liczb wymiernych możemy określić zbiór liczb niewymiernych. Są to wszystkie liczby (oczywiście rzeczywiste, o których zresztą powiemy później), które nie można zapisać w postaci ułamka zwykłego, gdzie licznik i mianownik jest liczbą całkowitą. Innymi słowy są to te liczby, które nie mogliśmy wepchać do liczb wymiernych. Przykładem liczby niewymiernej będzie liczba π, czyli na szczęście nie będzie „bezdomna". Z kolei nie będzie liczbą niewymierną liczba 1, 2, 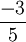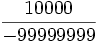$\frac{-3}{5}$ , $\frac{10000}{-99999999}$ , czy też 2,7563, bo już jest wymierna.

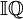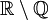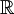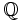Zbiór liczb niewymiernych będziemy oznaczać przez $\mathbb{IQ}$ lub częściej $\mathbb{R} \setminus \mathbb{Q}$ jako, że zbiór ten można otrzymać przez odjęcie od zbioru liczb rzeczywistych $\mathbb{R}$ wszystkich liczb wymiernych $\mathbb{Q}$ .

Zbiór liczb rzeczywistych

Wszystkie zbiory liczb opisane wyżej możemy włożyć do jednego worka, do liczb rzeczywistych. Można nawet powiedzieć, że wszystkie liczby wymierne i niewymierne tworzą zbiór liczb rzeczywistych. Przykładem może być 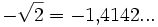$-\sqrt{2} = -1{,}4142...$ , 5, π = 3,14... czy też -2. Czym się charakteryzują wszystkie liczby rzeczywiste? Otóż posiadają one w zapisie dziesiętnym cyfry od 0 do 9, mogą posiadać znak minus i przecinek, ale nic poza tym. Hmm, a jaka liczba nie spełnia tych warunków? Otóż w matematyce istnieją różne twory... chociażby chyba najprostszy nadzbiór liczb rzeczywistych - liczby zespolone (oznaczane przez 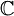$\mathbb{C}$ ), o których najprawdopodobniej nie dowiesz się na poziomie liceum.

Zbiór liczb rzeczywistych oznaczamy przez 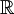$\mathbb{R}$ .

Treść udostępniana na licencji GNU Free Documentation License . Źródło: Wikibooks

Autor: Wikibooks

nauka zbiory matematyka