 | DEFINICJA Prawem rachunku zdań nazywamy zdanie złożone, które jest zawsze prawdziwe np. |
Rzeczywiście zdanie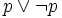 
jest zawsze prawdziwe. Mówiąc „Byłem w kinie lub nie byłem w kinie” nie skłamiemy. Prawo rachunku zdań nazywane jest też prawem logicznym lub tautologią. Innym przykładem zdania, zawsze prawdziwego jest zdanie „jeśli nieprawdą jest, że jadłem śniadanie lub nie jadłem obiadu, to nie jadłem śniadania i jadłem obiad”.
Ale jak sprawdzić, czy dane zdanie jest prawdziwe? Możemy do tego wykorzystać metodę „zero-jedynkową”. Zacznijmy od przykładu podanego na samym początku, czyli zdania 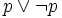. Najlepiej utworzyć do tego odpowiednią tabelkę i analizujemy wszystkie możliwości. W przypadku prostego zdania p mamy tylko dwie możliwości -- jego wartość logiczna może wynosić albo 1 albo 0; czyli w tabelce pod p wstawiamy 1 i 0 i wyliczamy wartości logiczne poszczególnych zdań, które dodaliśmy do tabelki.
| p | ¬p | p ∨ ¬p |
|---|---|---|
| 1 | 0 | 1 |
| 0 | 1 | 1 |
Zobaczmy kolejny przykład. Udowodnimy, że zdanie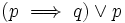 
jest tautologią. Najpierw w pierwszej (p) i w drugiej kolumnie (q) wypisujemy wszystkie możliwości, których tym razem będzie cztery.
| p | q | (p ⇒ q) | (p ⇒ q) ∨ p |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 |
Ponieważ zdanie 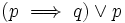jest zawsze prawdziwe (pokazuje nam to ostatnie kolumna, po prawej stronie), możemy wywnioskować, że jest tautologią (czyli prawem rachunku zdań).
A jak pokazać, że zdanie „jeśli nieprawdą jest, że jadłem śniadanie lub nie jadłem obiadu, to nie jadłem śniadania i jadłem obiad” jest „politycznie poprawne”, czyli zawsze prawdziwe. Nawet intuicyjnie ciężko jest zrozumieć to zdanie, więc musimy je przerobić na zapis matematyczny. Mamy dwa zdania proste:
- p: jadłem śniadanie
- q: jadłem obiad.
Zdanie podrzędne „nieprawdą jest, że jadłem śniadanie lub nie jadłem obiadu” zapiszemy jako:
,
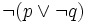a zdanie „nie jadłem śniadania i jadłem obiad” jako:
.
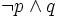Czyli całe zdanie przybierze postać:
.
Teraz tworzymy tabelę dla tego „logicznego giganta” i sprawdzamy wszystkie możliwości.
| p | q | ¬p | ¬q | p ∨ ¬q | ¬(p ∨ ¬q) | ¬p ∧ q | ¬(p ∨ ¬q) ⇒ (¬p ∧ q) |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
No dobra, ale jak najłatwiej wypisać wszystkie możliwości, gdy zdanie składa się z wielu zmiennych np. z trzech p, q, r. Zobaczmy najpierw, jakby wyglądał początek takiej tabelki.
| p | q | r | ... |
|---|---|---|---|
| 1 | 1 | 1 | ... |
| 1 | 1 | 0 | ... |
| 1 | 0 | 1 | ... |
| 1 | 0 | 0 | ... |
| 0 | 1 | 1 | ... |
| 0 | 1 | 0 | ... |
| 0 | 0 | 1 | ... |
| 0 | 0 | 0 | ... |
Widzimy, że mamy 8 = 23 możliwości. Teraz jak je wypisać? Hmm... na samej górze mamy same jedynki, pod kolumną r mamy od góry 1, 0, 1, 0, 1 itp., czyli wartości co chwilę zmieniają, pod kolumną q wartości się zmieniają co dwa, a pod kolumną p co cztery. Czyli już mamy sposób:
- na samej górze dajemy same jedynki,
- pod trzecią kolumną (r) zmieniamy wartości co jeden,
- pod drugą kolumną (q) zmieniamy wartości co dwa,
- pod pierwszą kolumną (p) zmieniamy wartości co cztery.
Sytuacja dla czterech, pięciu, czy sześciu zmiennych będzie bardzo podobna, tylko gdzieniegdzie będzie trzeba zmieniać wartość co osiem, co szesnaście itp.
Czy zdanie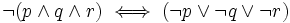 
jest tautologią? Sprawdźmy.
| p | q | r | ¬p | ¬q | ¬r | p ∧ q ∧ r | ¬(p ∧ q ∧ r) | ¬p ∨ ¬q ∨ ¬r | ¬(p ∧ q ∧ r) ⇔ (¬p ∨ ¬q ∨ ¬r) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
Ponieważ zdanie to ma zawsze wartość logiczną równą 1, więc jest prawem rachunku zdań.
Prawa De Morgana
Na koniec przedstawimy prawa De Morgana dotyczące zaprzeczeń zdań złożonych:
- I prawo De Morgana:
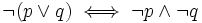
- (Zaprzeczenie alternatywy dwóch zdań jest równoważne koniunkcji zaprzeczeń tych zdań)
- II prawo De Morgana:
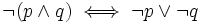
- (Zaprzeczenie koniunkcji dwóch zdań jest równoważne alternatywie zaprzeczeń tych zdań)
Prawa te są oczywiście tautologiami. W ćwiczeniu ??? zostaniesz poproszony o udowodnienie tych praw.
Jak napisać zdanie „każdy pies ma cztery łapy” lub „są ludzie, którzy nie umieją liczyć”? W następnym podrozdziale dowiemy się, jak pisać zdania takiego typu, czyli zdania odnoszące się do własności pewnego zbioru. Dowiemy się, co oznacza tajemnicze słowo „kwantyfikator”...
Treść udostępniana na licencji GNU Free Documentation License . Źródło: Wikibooks.pl
Autor: Wikibooks