Wektor - definicja
Wektorem nazywamy uporządkowaną parę punktów. Pierwszy z nich to początek, drugi - koniec wektora. Odległość między początkiem i końcem wektora nazywamy jego długością. Wektor, którego początkiem i końcem jest ten sam punkt nazywamy wektorem zerowym.
Podczas opisywania wektora należy podać 4 jego własności:
- kierunek - prosta na której leży wektor
- zwrot - początek i koniec wektora
- wartość
- punkt przyłożenia
Działania na wektorach
a) dodawanie
Przy dodawaniu wektorów stosuje się dwie metody: metodę równoległoboku lub metodę wielokąta.
Metoda równoległoboku polega na zbudowaniu równoległoboku z dwóch wektorów. Przekątna, której jeden z końców znajduje się w miejscu przyłożenia obydwu wektorów, jest szukanym wektorem wypadkowym.
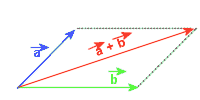
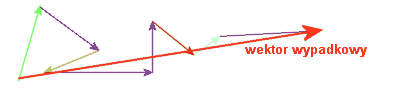
Metoda wielokąta jest bardzo przydatna przy dodawaniu większej ilości wektorów, poza tym jest prostsza od metody równolegloboku. W miejscu, gdzie kończy się jeden wektor, rysujemy kolejny. Początkiem wypadkowego wektora jest początek pierwszego z dodawanych wektorów, zaś jego końcem jest koniec ostatniego z dodawanych wektorów.
b) odejmowanie
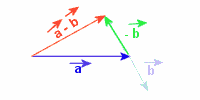
Odejmowanie wektorów a i b sprowadza się do dodania wektorów a i -b, czyli wektora o przeciwnym zwrocie w stosunku do b:
c) mnożenie wektora przez skalar
Mnożenie wektora a przez skalar n daje w wyniku nowy wektor na o wartości liczbowej n razy powiększonej i o zwrocie zgodnym lub przeciwnym względem wektora a, zależnie od tego, czy skalar n jest dodatni, czy ujemny.
d) mnożenie wektora przez wektor
Przy mnożeniu wektora przez wektor rozróżniamy iloczyn skalarny i iloczyn wektorowy.
- iloczyn skalarny
Iloczyn skalarny wektorów a i b oznaczamy symbolicznie a . b. Iloczyn skalarny dwóch wektorów jest skalarem, którego wartość liczbowa jest równa iloczynowi wartości liczbowych danych wektorów przez cosinus kąta zawartego między nimi, czyli:
- iloczyn wektorowy
Iloczyn wektorowy wektorów a i b oznaczamy symbolicznie a x b. Iloczyn ten jest nowym wektorem o określonej umownie wartości liczbowej i kierunku.
a x b = c
Wartość liczbowa wektora c równa się iloczynowi wartości wektorów a przez b przez sinus kąta zawartego między nimi:
Punkt przyłożenia wektora c pokrywa się z początkami wektorów a i b. Kierunek jego jest prostopadły do płaszczyzny zawierającej wektory a i b. Zwrot wektora c jest określony regułą śruby prawoskrętnej, zwanej również regułą korkociągu. Korkociąg ustawiamy prostopadle do płaszczyzny wektorów a i b opierając jego ostrze w punkcie O. Rączkę korkociągu ustawiamy równolegle do pierwszego wektora wymienionego w iloczynie wektorowym, a więc w naszym przykładzie do wektora a. Obracamy rączkę tak, aby po skręceniu o kąt α zajęła ona położenie równoległe do wektora b. Podczas tego obrotu ostrze przesuwa się w określonym kierunku, który umownie przyjęto za zwrot wektora c.
Źródło: http://www.superfizyka.za.pl/
