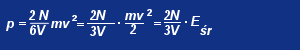WPROWADZENIE DO TEORII KINETYCZNO - MOLEKULARNEJ
Teorii kinetyczno-molekularnej zawdzięczamy specjalne, "mikroskopowe" ujęcie zjawisk zachodzących w otaczającym nas świecie. Teoria ta opiera się na następujących założeniach ogólnych:
1. Ciała mają budowę nieciągłą; składają się z drobnych elementów w postaci atomów lub cząsteczek (molekuł)
2. Wymienione elementy są w ciągłym ruchu. Wartości liczbowe i kierunki prędkości poszczególnych elementów są różne.
3. Pomiędzy poszczególnymi elementami budowy ciał występują siły wzajemnego oddziaływania.
Ujęcie właściwości gazów z punktu widzenia teorii kinetycznej przedstawia się najprościej z tego względu, że dzięki stosunkowo dużym średnim odległościom międzycząsteczkowym w gazie można w pierwszym przybliżeniu zaniedbać siły wzajemnego oddziaływania cząsteczek. Właśnie dzięki temu w dalszych rozważaniach będę mógł założyć, że każda cząsteczka gazu porusza się swobodnie (bez działania sił) aż do momentu zderzenia z inną cząsteczką albo ze ścianka naczynia. Stąd wniosek, że odcinki drogi między kolejnymi zderzeniami są przebywane ruchem jednostajnym prostoliniowym.
CIŚNIENIE GAZU Z PUNKTU WIDZENIA TEORII KINETYCZNEJ
W rozdziale tym wyprowadzam jeden z podstawowych wzorów teorii kinetyczno-molekularnej gazów - równanie, które wyraża związek pomiędzy ciśnieniem, a wielkościami cząsteczkowymi:
Szukamy ciśnienia jakie wywierają cząsteczki gazu na ścianki sześcianu o boku l
ZAŁOŻENIA:
- gaz jednorodny, doskonały
- cząsteczki poruszają się ze stałą prędkością
- naczynie jest sześcianem o boku l
- pomijamy oddziaływania zewnętrzne
- wewnątrz naczynia cząsteczki zderzają się sprężyście
Na początek dodatkow zakładam, że cząsteczki gazu poruszają się w jednakowym kierunku i wywierają ciśnienie na tylko jedną ściankę naczynia.
Najpierw znajduję siłę f z jaką jedna cząsteczka działa na ściankę naczynia:
Z II zas. dynamiki:
Δp = mv - (-mv) = 2mv
f = (2mv)/t gdzie:
m - masa cząsteczki
v - prędkość cząsteczki
t - czas w jakim cząsteczka przebywa drogę od jednej ścianki naczynia do drugiej - l
Całkowita siła F, którą na ściankę naczynia działa N cząsteczek można zatem zapisać:
F=Nf = N . (2mv)/t Dzięki równaniu drogi w ruchu jednostajnym możemy wyznaczyć t: l = v . t => t = l / vF= N . (2mv2)/l
Ponieważ wiadomo, że ciśnienie to siła działająca na powierzchnię, możemy obliczyć ciśnienie p1 wywierane przez N cząsteczek na ściankę naczynia (S = l2): p' = F/S = N . (2mv2) / l3 = N . (2mv2) / V V - objętość naczynia
Ponieważ p' jest to ciśnienie, które wywierałby gaz działając tylko na jedną ściankę naczynia, a naczynie posiada 6 ścianek, zatem rzeczywiste ciśnienie p jest równe:
p = p'/6 = (2Nmv2)/(6V) (mv2)/2 to znany wzór na energię kinetyczną. Zapisane to zostało jako energia średnia, gdyż energia kinetyczna jednej cząsteczki może zmienać się w wyniku zderzeń z innymi cząsteczkami, ale średnia energia kinetyczna cząsteczek nie ulega zmianie (zgodnie z zasadą zachowania energii).Zależność, którą otrzymaliśmy jest to podstawowy wzór teorii kinetyczno-molekularnej, ukazujący zależność ciśnienia od energii średniej.(ale ładnie to ująłem prawda? :)
Źródło: http://www.superfizyka.za.pl/