PRACA W TERMODYNAMICE
Samo pojęcie pracy można spotkać w mechanice i jest ono tam dokładnie omówione. Tutaj omówię tylko szczegóły związane z pracą w różnych procesach termodynamicznych.Załóżmy, że w naczyniu zamkniętym nieruchomym tłokiem znajduje się n moli gazu doskonałego. Na tłok zaczęła działać siła F i przesunęła go o l. Zatem: W = Fh Ze statyki wiemy, że siła jest równa iloczynowi ciśnienia i powierzchni, na które to ciśnienie jest wywierane, a więc: F = pS
W = pSh Z matematyki wiadomo, że objętość to pole powierzchni razy wysokość: W = pΔV
Jednak ta zależność jest prawdziwa tylko dla przemiany izobarycznej, poniewać w przemianie izochorycznej zmiana objętości jest równa 0, a więc i W = 0. Natomiast w przemiane izotermicznej zmianie ulega i ciśnienie i objętość, więc sprawa jest znacznie bardziej skomplikowana. Przemiana adiabatyczna jest znacznie prostsza ponieważ W = ΔU = nCvΔt ( ale o tym poniżej)
ENERGIA WEWNĘTRZNA
Energia wewnętrzna - definicja
Energią wewnętrzną nazywamy wielkość charakteryzującą stan danego ciała lub układu ciał, która jest równa sumie wszystkich rodzajów energii cząsteczek i atomów, które tworzą ten układ.
Bardzo mądra definicja, prawda? Jednak to nie jest wcale takie trudne jakby się mogło wydawać. Każdy atom, czy cząsteczka porusza się, zatem posiada energię kinetyczną, jest pod wpływem różnych sił chociażby siły elektromagnetyczne wiązań chemicznych, zatem posiada energię potencjalną. Suma tych wszystkich energii jakie posiadają wszystkie cząsteczki wchodzące w skadad danego ciała to właśnie energia wewnętrzna.
Wartość energii wewnętrznej nie jest istotna, ale zazwyczaj fizyków obchodzi jej zmiana, która zachodzi podczas różnorakich procesów termodynamicznych. Zmiana ta może odbywać się na dwa sposoby: zmienia się temperatura układu ( zmianie ulega energia kinetyczna cząsteczek) lub też stan skupienia ciała (wtedy temperatura pozostaje stała, ale zmieniają się odległości pomiędzy cząsteczkami, a co za tym idzie zmianiają się wartości oddziaływań między nimi).
Zmiana zawsze jest równa:
gdzie:
n - liczba moli
Cv - ciepło wł. przy stałej objętości (dokłaniej omówione poniżej)
Δt - zmiana temperatury
BILANS CIEPLNY
Załóżmy, że mamy dwa ciała, jedno cieplejsze i jedno chłodniejsze w izolowanym termicznie układzie. Po pewnym czasie obydwa ciała będą miały tą samą temperaturę. Jak to wytułmaczyć? Jeśli dwa ciała zetkną się ze sobą, to ich cząsteczki będą się ze sobą zderzały i przekazywały sobie nawzajem energię. Z czasem następuje wyrównanie średnich prędkości między cząsteczkami ciał, a co za tym idzie ich temperatur. Ten sposób przekazywania energii nazwano cieplnym przekazem energii lub przepływem ciepła
Ciepło - definicja
Ciepło jest to wielkość fizyczna, która charakteryzuje proces cieplnego przekazu energii, równa jest wielkości przekazywanej energii.
Ponieważ ciepło jest to ilość przekazanej energii, jego jednostką jest oczywiście dżul [J].
Ciepło właściwe - definicja
Ciepło właściwe jest to stosunek energii, dostarczonej w wyniku cieplnego przekazu energii do masy ciała i przyrostu temperatury:
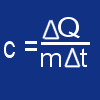Po zapoznaniu się z powyższymi pojęciami można przejść do właściwego bilansu cieplnego. Załóżmy, że m1 oznacza masę cieplejszego ciała, a m2 masę ciała chłodniejszego. c1 , c2 ciepła właściwe tych ciał, a t1, t2 temperatury początkowe.
Ciepło, które ciało cieplejsze oddało ciału zimniejszemu oznaczamy jako Q1, a ciepło, które pobrało ciało zimniejsze jako Q2.
Obydwa te ciepła są równe zmianie energii wewnętrznej poszczególnych ciał: Q1 = ΔU1 = c1m1(t1 - tk)
Q2 = ΔU2 = c2m2(tk - t2) tk - temperatura końcowa.
Nie trzeba chyba tłumaczyć, że ciepło oddane przez ciało cieplejsze jest równe ciepłu pobranemu przez ciało zimniejsze.
Q1 = Q2 Porównując te dwa ciepła można obliczyć np. temperaturę końcową. obydwu ciał.I ZASADA TERMODYNAMIKI. PRZEMIANY GAZOWE
Zanim przejdę do rzeczy przypomnę, że energia wewnętrzna jest funkcją stanu układu, zależną od jego parametrów, natomiast ciepło i praca są formami przekazywania energii. I zasada termodynamiki wiąże te trzy pojęcia:
I zasada termodynamiki
Zmiana energii wewnętrznej ciała lub układu ciał jest równa przekazanej energii w wyniku wykonanej pracy (nad ciałem lub przez ciało) i przepływu ciepła
Q > 0 - ciepło jest dostarczane do układu
Q < 0 - układ oddaje ciepło
W > 0 - do układu dostarczona jest energia w wyniku pracy W < 0 - układ wykonuje pracę kosztem energii wewnętrznej
Rozpatrzmy teraz przemiany gazowe z punktu widzenia I zasady termodynamiki:
Przemiana izochoryczna
Zakładam, że w naczyniu znajduje się n moli gazu doskonałego. Gaz ten ogrzewam, a ponieważ naczynie nie zwiększa swojej objętości, to również gaz się nie rozszerza. Jego temperatura zwiększa się od t1 do t2. Wzrasta również ciśnienie gazu z p1 do p2.
Ponieważ zmianie nie uległa objętość gazu, nie można mówić tu o pracy, zatem, zgodnie z I zasadą termodynamiki, dostarczone ciepło jest równe zmianie energii wewnętrznej:
W = 0 gdzie Cv to molowe ciepło właściwe gazu przy stałej objętości (równe energii, jaką należy dostarczyć jednemu molowi danego gazu, aby zwiększyć jego temperaturę o 1 stopień w przemianie izochorycznej).
Przemiana izobaryczna
Zakładam, że w naczyniu zamkniętym nieruchomym tłokiem znajdujesię n moli gazu doskonałego. Ogrzewam gaz przez dostarczenie ciepła Q, w wyniku czego temperatura zwiększa się o Δt, natomiast objętość rośnie o ΔV. I zasada termodynamiki dla tej przemiany wygląda następująco:
Q = nCpΔt
W = pΔV przyczym Cp to molowe ciepło właściwe gazu przy stałym ciśnieniu (równe energii, jaką należy dostarczyć jednemu molowi danego gazu, aby zwiększyć jego temperaturę o 1 stopień w przemianie izobarycznej).
Zastanówmy się, jaka jest zależność między Cp a Cv. Zapiszmy jeszcze raz I zasadę termodynamiki, ale podstawiając już odpowiednie wyrażenia: nCvΔt = pΔV - nCpΔt Zapiszmy teraz dwa równania Clapeyrona dla gazu przed przemianą i po przemianie: pV1 = nRt1
pV2 = nRt2 Dodając je stronami otrzymujemy: pΔV = nRΔt Podstawiamy do I zas. termodynamiki i otrzymujemy: nCvΔt = nRΔt - nCpΔt
nΔt Cv = nΔt ( R - Cp)
R = Cp - Cv
Przemiana izotermiczna
W naczyniu z ruchomym tłokiem znajduje się n moli gazu doskonałego. Ponieważ jak sama nazwa przemiany wskazuje temperatura nie zmienia się, więc zmiana energii wewnętrznej jest równa 0:
Przemiana adiabatyczna
W przemianie adiabatycznej nie ma wymiany ciepła z otoczeniem. Zatem energia wewnętrzna jest równa pracy:
Źródło: http://www.superfizyka.za.pl