Marcin Miczek
Instytut Fizyki, Politechnika Śląska w Gliwicach
Prowadząc kilka lat temu ćwiczenia rachunkowe z fizyki dla studentów Wydziału Chemicznego Politechniki Śląskiej w Gliwicach do wykładu prowadzonego przez Stanisława Kochowskiego (obecnie profesora Politechniki Śląskiej), rozwiązywałem ze studentami takie oto zadanie1
Izaak Newton urodził się w 1643 roku w niewielkiej miejscowości w hrabstwie Lincolnshire. Albert Einstein urodził się w 1879 r. w Ulm. Odległość między tymi miejscowościami wynosi około 800 km. Czy istnieje układ odniesienia, w którym obaj fizycy urodziliby się: a) równocześnie, b) w tym samym miejscu? Określić, z jaką prędkością układ ten musi poruszać się względem powierzchni Ziemi.
Zadanie to można rozwiązywać różnymi sposobami, dla mnie było ono zwykle okazją do wyjaśnienia pojęcia interwału czasoprzestrzennego (wprowadzonego wcześniej na wykładzie). Chciałbym opisać tu swe kilkuletnie doświadczenia dydaktyczne przy rozwiązywaniu tego zadania. Ponieważ reakcja studentów była rokrocznie taka sama, daje to trochę do myślenia o tym, jak uczyć teorii względności. Skorzystajmy zatem z pojęcia interwału czasoprzestrzennego:
![]()
gdzie c oznacza szybkość światła w próżni, t - czas, x, y, z - współrzędne przestrzenne. Wartość Δs2 nie zależy od wyboru inercjalnego układu odniesienia, co można sprawdzić wprost z transformacji Lorentza - jest to tzw. niezmiennik tej transformacji.
Obliczmy tenże interwał między dwoma podanymi w zadaniu zdarzeniami2 (indeks N odnosi się do Newtona, E - do Einsteina):
![]()
Okazuje się, że jest to tzw. interwał czysto czasowy (Δs2 > 0), a zatem nie istnieje układ odniesienia, w którym Newton i Einstein urodziliby się w tym samym czasie (bo w takim układzie odniesienia Δs2 ≤ 0, co jest w naszym przypadku niemożliwe), natomiast istnieje taki, w którym urodzili się w tym samym miejscu. Po dojściu do tegoż wniosku i zaakceptowaniu go (na razie czysto matematycznym) przez studentów zadaję pytanie: „Z jaką szybkością musi się poruszać względem Ziemi ów układ odniesienia, w którym Newton i Einstein urodzili się w tym samym miejscu?” Jakiej odpowiedzi spodziewalibyście się Państwo po studentach, którzy są świeżo po wykładzie z teorii względności i przerobili już parę przykładów z wydłużenia czasu i skrócenia długości? A jakżeby inaczej - „Z szybkością bliską szybkości światła!” A ja wtedy z szelmowskim uśmiechem powiadam: „A więc sprawdźmy”. Wypisanie transformacji Lorentza jest dość proste:
Szukamy szybkości v, dla której xN' = xE'. W trakcie obliczeń skróceniu ulega czynnik γ, przez co wynik nie różni się od tego, który otrzymalibyśmy stosując transformację Galileusza, w której γ=1. Żądana szybkość wynosi:
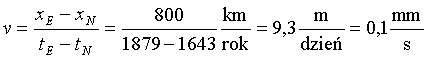
Dla porównania szybkość ślimaka jest rzędu 1 mm/s. Ten zaskakujący dla studentów wynik tłumaczyłem w sposób następujący. Wyobraźmy sobie rakietę z kosmitą, który w 1643 r. znajduje się w miejscu urodzin Newtona i przez okienko swego pojazdu obserwuje narodziny twórcy klasycznej dynamiki. Następnie rakieta porusza się z obliczoną przez nas szybkością, aby w 1879 r. znaleźć się nad Ulm - wtedy kosmita przez okienko rakiety obserwuje narodziny twórcy teorii względności. I konkludując z uśmiechem oświadczam, że narodziny obu fizyków odbyły się w tym samym miejscu (w układzie odniesienia związanym z rakietą) - a mianowicie naprzeciw okienka rakiety. Zaś cały problem nie leży w rozpędzeniu rakiety do ogromnej szybkości, a w długości życia naszego obserwatora.
No i jak Państwo myślicie - co na to wszystko studenci? No cóż, zwykle odpowiadają „To jest bez sensu”. Chyba rozwiązanie okazało się zbyt banalne - cóż to za relatywistyka przy takiej podślimaczej szybkości.
Kończąc już bardziej poważnie - widać, że pojęcie układu odniesienia okazuje się zaskakująco trudne dla studentów pierwszego roku, usłyszenie zaś na wykładzie o zadziwiających efektach relatywistycznych przesłania o wiele bardziejfundamentalny i zdroworozsądkowy charakter zasady względności Galileusza.
1 Zadanie zostało zaczerpnięte z książki: Jadwiga Salach, Barbara Sagnowska, Jerzy M. Kreiner, „Fizyka z astronomią. Podręcznik dla liceum ogólnokształcącego. Klasa II.” Wydawnictwa Szkolne i Pedagogiczne, Warszawa 1989 (zadanie 36.6 strona 115), zatem artykuł może przydać się także nauczycielom szkółponadgimnazjalnych.
2 Interwał czasoprzestrzenny jest obliczany jak w układzie inercjalnym. Poprawki związane z ziemskim polem grawitacyjnym oraz dobowym i rocznym ruchem Ziemi można obliczyć z ogólnej teorii względności, są one jednak w tym przypadku zaniedbywalne.
