Patrząc z pewnego punktu widzenia można dostrzec, że trzy zasady dynamiki Newtona to w istocie jedna zasada, która została rozpisana na "trzy punkty". Z tego punktu widzenia druga zasada dynamiki - głosząca, że siła jest proporcjonalna do przyśpieszenia, które ona powoduje - jest tylko definicją siły. Po prostu, definicja ta przedstawia propozycję "umowy naukowej" - proponuje ona, aby słowem "siła" nazywać pewien iloczyn, a mianowicie, siła F=m*a.
Z jakiego punktu widzenia jest to widoczne? Widać to, jeśli za podstawę rozważań przyjąć grawitacyjne prawo Galileusza, które mówi, że w polu grawitacyjnym wszystkie ciała spadają z jednakowym przyśpieszeniem. To znaczy, że przyśpieszenie spadku ciał o różnych masach nie zależy od mas tych ciał, lecz zależy od pola i masy ciała, które jest przyczyną przyśpieszenia dla spadających ciał. Dlatego przy wyborze odpowiedniej funkcji do opisu centralnie-symetrycznego pola wystarczy, aby przyśpieszenie było proporcjonalne do wielkości masy przyśpieszającego ciała, a wówczas pozostała część funkcji może mieć dowolną postać.*)
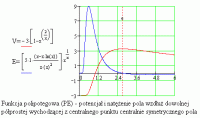
Niech przyśpieszenie będzie opisane za pomocą wzoru E=M*Ej - jest to jednocześnie wzór opisujący natężenie pola, które jest przyczyną przyśpieszenia. Jest to wzór opisujący przyśpieszenie i natężenie pola wzdłuż dowolnej półprostej, jaka "wychodzi" z centralnego punktu pola. W tym wzorze M jest masą ciała (pola) będącego przyczyną przyśpieszenia, natomiast Ej jest przyśpieszeniem (innych ciał) w polu pochodzącym od ciała z jednostkową masą, czyli kiedy we wzorze E=M*Ej podstawić M=1, wychodzi Ej=1*Ej.
Zatem przyśpieszenie ciała w polu o masie M1 jest równe E1=M1*Ej, a przyśpieszenie ciała w polu o masie M2 jest równe E2=M2*Ej. Niech dwa ciała o masie M1 i M2 znajdują się w pewnej odległości od siebie i nadają sobie nawzajem przyśpieszenia. Wówczas ciało o masie M1 będzie miało przyśpieszenie E2=M2*Ej, a ciało o masie M2 będzie miało przyśpieszenie E1=M1*Ej. A jaki będzie w obu przypadkach iloczyn masy przyśpieszanego ciała i jego przyśpieszenia?
Dla ciała o masie M1 iloczyn masy i przyśpieszenia wynosi M1*E2=M1*M2*Ej (bo przyśpieszenie jest powodowane przez ciało o masie M2), natomiast dla ciała o masie M2 iloczyn masy i przyśpieszenia będzie równy M2*E1=M2*M1*Ej (bo przyśpieszenie jest powodowane przez ciało o masie M1). Można tu zauważyć, że iloczyny te są równe.
Jeżeli do tego zastosować definicję - czyli treść drugiej zasady Newtona - która mówi, że F1=M1*a1 oraz F2=M2*a2 (przy czym a1=E2 oraz a2=E1), to można zapisać, że F1=M1*M2*Ej oraz F2=M2*M1*Ej. Zwykle w matematycznym opisie uwzględnia się przeciwne kierunki przyspieszeń ciał o masie M1 i M2, więc w zapisie równość ta przedstawiana jest w postaci F1=-F2. Ta równość nazywa się trzecią zasadą dynamiki - w opisie słownym brzmi ona następująco: wzajemne oddziaływania na siebie dwóch ciał są sobie równe i przeciwnie skierowane.
Tutaj trzeba na moment powrócić do miejsca w tekście, które jest zaznaczone jako *). Mówi się tam, że pozostała część funkcji przyśpieszenia c.s. pola E=M*Ej, czyli część zapisana jako Ej, może mieć dowolną postać. Ale należy tu zwrócić uwagę na to, że w logicznym wywodzie (i w definiowaniu) wzorów, które znajdują się w zasadach dynamiki Newtona, wykorzystana jest jedna i ta sama część Ej, a nie różnorodne. To znaczy, wszędzie jest mowa o tej samej części Ej, a nie o częściach Ej1, Ej2, Ej3... Mówiąc inaczej, ta część funkcji może mieć różnorodną postać, ale jeśli do wywodu przyjmuje się jakąkolwiek z nich, to taka część funkcji w logicznym wywodzie zasad Newtona już się nie zmienia.
W takim przypadku można powiedzieć, że do wyprowadzenia zależności, które są znane jako zasady dynamiki Newtona, milcząco przyjmuje się postulat, który mówi, że wszystkie c.s. pola zmieniają się według jednej i tej samej matematycznej formuły. Najważniejszym skutkiem tego postulatu jest to, że zasady dynamiki Newtona są akurat takie, jakie są. To znaczy, w procesach, które przebiegają z zachowaniem zasad dynamiki Newtona, wspólny środek ciężkości obiektu pozostaje nieruchomy i ilość energii układu nie ulega zmianie.
Ale można spodziewać się, i wiele faktów wskazuje na to, że przyroda posiada także i "drugą stronę medalu", którą można opisywać za pomocą zasad opierających się na innym postulacie. W tym innym postulacie część składowa funkcji przyśpieszenia, oznaczana jako Ej, dla różnych c.s. pól ma różnorodną matematyczną postać, to znaczy, dla różnych c.s. pól powinna ona być zapisana jako Ej1, Ej2, Ej3... W takim przypadku, w procesie z takimi obiektami, niejako z powodu natury c.s. pól (obiektów), wspólny środek ciężkości porusza się samoczynnie i, oczywiście, samoczynnie zmienia się ilość energii układu.
Komputerowy program wykonawczy Gravo2S.exe służy do graficzno-dynamicznego ilustrowania zarówno praw dynamiki Newtona, jak i praw dynamiki SRM (samoczynnego ruchu materii). I jedne, i drugie prawa są w tym programie prezentowane w taki sam sposób. A mianowicie, ciała (cząstki, centralnie symetryczne pola) przyśpieszają siebie nawzajem na tej samej zasadzie – można też powiedzieć, że w ich zachowaniu przejawia się Fundamentalna zasada materii.
W programie Gravo2S – na jego ekranie – można obserwować zachowanie dwóch cząstek na tle wykresu potencjału swojego sąsiada. Na podstawie obserwacji można wyciągać wnioski.
Wykres potencjału, a także sam potencjał, jest jedynie pewnego rodzaju pojęciowo-matematycznym wybiegiem. Potencjał i jego wykres przydatny jest tutaj o tyle, że można go wykorzystać jako odzwierciedlenie pewnego obiektu fizycznego. A sam ten obiekt fizyczny można potraktować jako usprawiedliwienie i przyczynę, gdy przyjdzie tłumaczyć (gdyby ktoś o to zapytał), skąd bierze się ruch cząstek. Wówczas zjawisko można wyjaśniać w taki sposób, że przyśpieszenie zachodzi w wyniku oddziaływania pola potencjałowego sąsiedniej cząstki. Z tym, że to centralnie symetryczne pole potencjałowe oraz cząstka to jest jedna i ta sama rzecz, tylko określona innymi słowami.
Potencjał pola i samo centralnie symetryczne pole to są wtórne pojęcia i wtórne obiekty fizyczne, które należy rozumieć jako wydedukowane z jakiegoś pierwotnego pojęcia i obiektu fizycznego. Tym pierwotnym pojęciem i obiektem(!) jest ruch i przyśpieszenie, które można przedstawić za pomocą matematycznej funkcji. Tak naprawdę, to nie wiadomo, co porusza się. Ale porusza się... Bo ta rzecz – poruszając się sama, pod wpływem jakichś początkowo nie zrozumiałych dla nas przyczyn – porusza nasze zmysły. Na tej podstawie nauczyliśmy się rozpoznawać różne rzeczy i je nazywać. Na identycznej zasadzie określany jest ruch oraz samo istnienie obiektów w postaci centralnie symetrycznych pól... albo cząstek, albo ciał.
Matematyczna funkcja przyśpieszenia cząstki jest także nazywana funkcją natężenia pola, które to pole, formalnie rzecz biorąc, jest przyczyną przyśpieszenia cząstki. Ale należy tu odróżnić od siebie te dwie rzeczy. Bo funkcja przyśpieszenia jest związana z poruszającą się cząstką i jej dotyczy, natomiast funkcja natężenia pola dotyczy cząstki, która jest przyczyną przyśpieszenia tej poruszającej się cząstki.
Matematyczna funkcja przyśpieszenia, albo inaczej funkcja natężenia pola (bo pod względem matematycznej struktury jest to ta sama funkcja), jest matematycznie i formalnie związana z funkcją potencjału pola, czyli z rozkładem tego pola w przestrzeni. Funkcja potencjałowa pola powstaje jako wynik z całkowania funkcji natężenia pola, albo można powiedzieć inaczej, że funkcja natężenia pola jest pochodną z funkcji potencjału pola.
Właśnie z powodu wymienionych matematycznych zależności, podczas obserwacji zachowania cząstek na ekranie programu Gravo2S, tak pięknie są ze sobą zgrane ich ruchy na tle wykresów pola potencjałowego swoich sąsiadek.
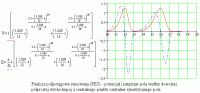
W programie Gravo2S można obserwować cząstki poruszające się zgodnie z funkcją przyśpieszenia. Ta funkcja występuje w kilku postaciach. Może ona mieć postać polipotęgową albo polipotęgową sumowaną. Funkcje polipotęgowe (PE) oraz funkcje polipotęgowe sumowane (PES) charakteryzują się tym, że za ich pomocą można tworzyć modele stabilnych układów strukturalnych – najprostszy układ składa się tylko z dwóch cząstek.
Funkcja PE charakteryzuje się tym, że za jej pomocą można opisywać centralnie symetryczne (c.s.) pole mające tylko jedną powłokę potencjałową. Przy dalszej odległości od centralnego punktu cząstki (c.s. pola) funkcja zmienia się podobnie jak funkcja grawitacyjna, czyli zmienia się w przybliżeniu odwrotnie proporcjonalnie do kwadratu odległości. Funkcja PES służy do opisu c.s. pól posiadających wiele powłok potencjałowych.
____________________________________
Odkrycie fizyki na trzecie tysiąclecie - http://pinopa.republika.pl/