
Naturalny system dwójkowy (ang. NBS - Natural Binary System) jest najprostszym systemem pozycyjnym, w którym podstawa p = 2. System posiada dwie cyfry 0 i 1, zatem można je kodować bezpośrednio jednym bitem informacji. Wartość liczby obliczamy zgodnie ze wzorem podanym w rozdziale o systemach pozycyjnych.
 | | |
| | |
| | |  Wartość dziesiętna liczby zapisanej w naturalnym kodzie binarnym Wartość dziesiętna liczby zapisanej w naturalnym kodzie binarnymbn-1bn-2...b2b1b0 = bn-12n-1 + bn-22n-2 + ... + b222 + b121 + b020 gdzie b - bit, cyfra dwójkowa 0 lub 1
n - liczba bitów w zapisie liczby | |
| | | | |

Obliczyć wartość liczby dwójkowej 11100101(2).
11100101(2) = 1 x 27 + 1 x 26 + 1 x 25 + 0 x 24 + 0 x 23 + 1 x 22 + 0 x 21 + 1 x 20
11100101(2) = 1 x 128 + 1 x 64 + 1 x 32 + 0 x 16 + 0 x 8 + 1 x 4 + 0 x 2 + 1 x 1
11100101(2) = 128 + 64 + 32 + 4 + 1
11100101(2) = 229(10)
Jeśli dokładnie przyjrzysz się powyższym obliczeniom, to na pewno zauważysz, iż w systemie binarnym w celu obliczenia wartości liczby wystarczy po prostu zsumować wagi pozycji, na których cyfry przyjmują wartość 1.

101011(2) = 25 + 23 + 21 + 20 = 32 + 8 + 2 + 1 = 43(10)
Jest to znaczne uproszczenie w stosunku do innych systemów, gdzie musimy wykonywać mnożenia cyfr przez wagi pozycji. Tutaj albo dana waga występuje w wartości liczby (cyfra 1), albo nie występuje (cyfra 0). Nie na darmo system binarny jest najprostszym systemem pozycyjnym.
Bardzo ważne dla informatyka i programisty jest nauczenie się na pamięć pierwszych szesnastu liczb binarnych:
| dziesiętnie | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| dwójkowo | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |

Określmy, jaką największą liczbę dwójkową możemy zapisać za pomocą n bitów (czyli cyfr binarnych). Największa liczba musi posiadać same cyfry 1, czyli w wartości liczby muszą uczestniczyć wszystkie wagi pozycji. Zatem:
| dla 1b mamy | 1(2) | = 1(10) |
| dla 2b mamy | 11(2) | = 2 + 1 = 3(10) |
| dla 3b mamy | 111(2) | = 4 + 2 + 1 = 7(10) |
| dla 4b mamy | 1111(2) | = 8 + 4 + 2 + 1 = 15(10) |
| ... | | |
Otrzymujemy kolejne liczby:
dla 1b mamy
dla 2b mamy
dla 3b mamy
dla 4b mamy
... | 1
3
7
15
|
Liczby te tworzą prosty ciąg potęgowy:
| dla 1b mamy | 1 | = 21 - 1 |
| dla 2b mamy | 3 | = 22 - 1 |
| dla 3b mamy | 7 | = 23 - 1 |
| dla 4b mamy | 15 | = 24 - 1 |
| ... | | |
Wykładnik potęgowy liczby 2 jest równy ilości bitów, zatem dla n bitów otrzymujemy wzór:
 | | |
| | |
| | |  Zakres n bitowej liczby w naturalnym kodzie dwójkowym wynosi Zakres n bitowej liczby w naturalnym kodzie dwójkowym wynosiZ(2) = <0, 2n - 1> | |
| | | | |

Jaką największą liczbę dziesiętną można przedstawić przy pomocy 64 bitów?
Odp.
264 - 1 = 18446744073709551616 - 1 = 18446744073709551615

Schemat Hornera pozwala obliczyć wartość liczby binarnej przy minimalnej ilości operacji arytmetycznych. W systemie binarnym schemat ten jest bardzo prosty:
| Schemat Hornera dla systemu binarnego |
Wejście: ciąg cyfr binarnych
Wyjście: W - wartość liczby reprezentowanej przez ciąg cyfr binarnychkrok 1: W 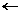 pierwsza cyfra pierwsza cyfra
krok 2: dopóki są kolejne cyfry wykonujemy operację W 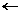 2 x W + kolejna cyfra 2 x W + kolejna cyfra
krok 3: Kończymy |
Operację mnożenia 2 x W możemy zastąpić dodawaniem W + W. Dodawanie komputer wykonuje o wiele szybciej od mnożenia.

Obliczyć schematem Hornera wartość liczby binarnej 111010111101(2)
cyfra 1: W = 1
cyfra 1: W = (1 + 1) + 1 = 3
cyfra 1: W = (3 + 3) + 1 = 7
cyfra 0: W = (7 + 7) + 0 = 14
cyfra 1: W = (14 + 14) + 1 = 29
cyfra 0: W = (29 + 29) + 0 = 58
cyfra 1: W = (58 + 58) + 1 = 117
cyfra 1: W = (117 + 117) + 1 = 235
cyfra 1: W = (235 + 235) + 1 = 471
cyfra 1: W = (471 + 471) + 1 = 943
cyfra 0: W = (943 + 943) + 0 = 1886
cyfra 1: W = (1886 + 1886) + 1 = 3773 - koniec
Kolejne od końca cyfry binarne zapisu liczby w systemie dwójkowym otrzymamy jako reszty z dzielenia tej liczby przez 2. Metoda ta została dokładnie opisana w rozdziale poświęconym przeliczaniu liczb dziesiętnych na zapis w innych systemach liczbowych.
| Algorytm wyznaczania cyfr zapisu dwójkowego liczby |
Wejście: W - wartość liczby
Wyjście: ciąg cyfr binarnych reprezentujących w systemie dwójkowym wartość Wkrok 1: kolejna cyfra 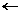 W mod 2, W W mod 2, W  W div 2 W div 2
krok 2: jeśli W > 0, wróć do kroku 1
krok 3: Wyprowadź otrzymane cyfry w kolejności odwrotnej do ich otrzymania
krok 4: Koniec |

Przeliczyć na system dwójkowy liczbę 582642(10).
| 582642 div 2 = | 291321 | i reszta 0 |
| 291321 div 2 = | 145660 | i reszta 1 |
| 145660 div 2 = | 72830 | i reszta 0 |
| 72830 div 2 = | 36415 | i reszta 0 |
| 36415 div 2 = | 18207 | i reszta 1 |
| 18207 div 2 = | 9103 | i reszta 1 |
| 9103 div 2 = | 4551 | i reszta 1 |
| 4551 div 2 = | 2275 | i reszta 1 |
| 2275 div 2 = | 1137 | i reszta 1 |
| 1137 div 2 = | 568 | i reszta 1 |
| 568 div 2 = | 284 | i reszta 0 |
| 284 div 2 = | 142 | i reszta 0 |
| 142 div 2 = | 71 | i reszta 0 |
| 71 div 2 = | 35 | i reszta 1 |
| 35 div 2 = | 17 | i reszta 1 |
| 17 div 2 = | 8 | i reszta 1 |
| 8 div 2 = | 4 | i reszta 0 |
| 4 div 2 = | 2 | i reszta 0 |
| 2 div 2 = | 1 | i reszta 0 |
| 1 div 2 = | 0 | i reszta 1 - koniec, wynik odczytujemy w kierunku z dołu do góry |
582642(10) = 10001110001111110010(2)

 | | |
| | |
| | | 
Poniższe, przykładowe programy są praktyczną realizacją omawianego w tym rozdziale algorytmu. Zapewne można je napisać bardziej efektywnie. To już twoje zadanie. Dokładny opis stosowanych środowisk programowania znajdziesz we wstępie. Programy przed opublikowaniem w serwisie edukacyjnym zostały dokładnie przetestowane. Jeśli jednak znajdziesz jakąś usterkę (co zawsze może się zdarzyć), to prześlij o niej informację do autora. Pozwoli to ulepszyć nasze artykuły. Będziemy Ci za to wdzięczni. | |
| | | | |
Program oblicza wartość liczby binarnej podanej jako ciąg cyfr. Ciekawostką jest to, iż ciąg ten nie jest ograniczony i może zawierać dowolną (w rozsądnych granicach) ilość cyfr binarnych. Wynik obliczany jest nie jako wartość liczbowa, lecz jako ciąg cyfr dziesiętnych. Dzięki temu nie jesteśmy ograniczani zakresem zmiennych całkowitych.
Wartość liczby binarnej obliczamy podanym powyżej schematem Hornera.
| Wydruk z uruchomionego programu |
Obliczanie wartości dziesiętnej
dowolnej liczby binarnej
===============================
(C)2005 mgr Jerzy Wałaszek
I LO w Tarnowie
Podaj liczbę binarną:
1110001011010101111101101010011111100010100010111110101010010111011111111010101
Wartość dziesiętna liczby binarnej:
535600877519892478934997
KONIEC. Naciśnij dowolny klawisz... |
| Microsoft Visual Basic 2005 Express Edition |
Borland
Delphi 7.0
Personal
Edition | // Obliczanie wartości dowolnej liczby dwójkowej
//----------------------------------------------
// (C)2005 mgr Jerzy Wałaszek
// I Liceum Ogólnokształcące
// im. K. Brodzińskiego
// w Tarnowie
//----------------------------------------------
program bindec;
{$APPTYPE CONSOLE}
var
bs,ds : string;
i,j,c,p,s : cardinal;
begin
writeln('Obliczanie wartosci dziesietnej');
writeln(' dowolnej liczby binarnej');
writeln('===============================');
writeln('(C)2005 mgr Jerzy Walaszek');
writeln(' I LO w Tarnowie');
writeln;
writeln('Podaj liczbe binarna:'); writeln; readln(bs);
writeln;
ds := '0'; i := 1;
while (i <= length(bs)) and (bs[i] in ['0'..'1']) do
begin
p := 0; // Przeniesienie
c := ord(bs[i]) - 48; // Cyfra binarna
for j := length(ds) downto 1 do
begin
// Schemat Hornera
s := 2 * (ord(ds[j]) - 48) + c + p;
c := 0;
// Wyznaczamy przeniesienie do następnej kolumny
p := s div 10;
// Cyfrę wynikową zapisujemy w miejscu docelowym
ds[j] := char((s mod 10) + 48);
// Jeśli po wyczerpaniu cyfr ds przeniesienie p ma wartość
// większą od zera, to jest ono równe pierwszej cyfrze
if (j = 1) and (p > 0) then ds := char(p + 48) + ds;
end;
// Następna cyfra binarna
inc(i);
end;
writeln('Wartosc dziesietna liczby binarnej:');
writeln;
writeln(ds);
writeln;
writeln('Nacisnij klawisz Enter...'); readln;
end. |
Borland
C++ Builder
6.0
Personal
Edition | // Obliczanie wartości dowolnej liczby dwójkowej
//----------------------------------------------
// (C)2005 mgr Jerzy Wałaszek
// I Liceum Ogólnokształcące
// im. K. Brodzińskiego
// w Tarnowie
//----------------------------------------------
#include <iostream>
#include <string>
using namespace std;
main()
{
string bs,ds;
int i,j,c,p,s;
char z[1];
cout << "Obliczanie wartosci dziesietnej\n"
" dowolnej liczby binarnej\n"
"===============================\n"
"(C)2005 mgr Jerzy Walaszek\n"
" I LO w Tarnowie\n\n"
"Podaj liczbe binarna:\n\n";
cin >> bs;
cout << endl;
ds = "0"; i = 0;
while((i < bs.length()) && ((bs[i] == '0') || (bs[i] == '1')))
{
p = 0; // Przeniesienie
c = bs[i] - 48; // Cyfra binarna
for(j = ds.length() - 1; j >= 0; j--)
{
// Schemat Hornera
s = 2 * (ds[j] - 48) + c + p;
c = 0;
// Wyznaczamy przeniesienie do następnej kolumny
p = s / 10;
// Cyfrę wynikową zapisujemy w miejscu docelowym
ds[j] = (char)((s % 10) + 48);
// Jeśli po wyczerpaniu cyfr ds przeniesienie p ma wartość
// większą od zera, to jest ono równe pierwszej cyfrze
if(!j && p) ds = (char)(p + 48) + ds;
};
// Następna cyfra binarna
i++;
};
cout << "Wartosc dziesietna liczby binarnej:\n\n"
<< ds << "\n\nNacisnij ENTER...\n";
cin.getline(z,1);
cin.getline(z,1);
} |
Microsoft
Visual
Basic 2005
Express
Edition | ' Obliczanie wartości dowolnej liczby dwójkowej
'----------------------------------------------
' (C)2005 mgr Jerzy Wałaszek
' I Liceum Ogólnokształcące
' im. K. Brodzińskiego
' w Tarnowie
'----------------------------------------------
Option Explicit On
Module Module1
Sub Main()
Dim bs, ds As String
Dim i, j, c, p, s As Integer
Console.WriteLine("Obliczanie wartości dziesiętnej")
Console.WriteLine(" dowolnej liczby binarnej")
Console.WriteLine("===============================")
Console.WriteLine("(C)2005 mgr Jerzy Wałaszek")
Console.WriteLine(" I LO w Tarnowie")
Console.WriteLine()
Console.WriteLine("Podaj liczbę binarną:")
Console.WriteLine()
bs = Console.ReadLine()
Console.WriteLine()
ds = "0" : i = 0
While (i < bs.Length())
If (bs.Chars(i) <> "0") And (bs.Chars(i) <> "1") Then Exit While
p = 0 ' Przeniesienie
c = Asc(bs.Chars(i)) - 48 ' Cyfra binarna
For j = ds.Length() - 1 To 0 Step -1
' Schemat Hornera
s = 2 * (Asc(ds.Chars(j)) - 48) + c + p
c = 0
' Wyznaczamy przeniesienie do następnej kolumny
p = s \ 10
' Cyfrę wynikową zapisujemy w miejscu docelowym
Mid(ds, j + 1, 1) = Chr((s Mod 10) + 48)
' Jeśli po wyczerpaniu cyfr ds przeniesienie p ma wartość
' większą od zera, to jest ono równe pierwszej cyfrze
If (j = 0) And (p > 0) Then ds = Chr(p + 48) + ds
Next
' Następna cyfra binarna
i += 1
End While
Console.WriteLine("Wartość dziesiętna liczby binarnej:")
Console.WriteLine()
Console.WriteLine(ds)
Console.WriteLine()
Console.WriteLine("KONIEC. Naciśnij dowolny klawisz...")
Console.ReadLine()
End Sub
End Module |
| Python | # -*- coding: cp1250 -*-
# Obliczanie wartości dowolnej liczby dwójkowej
#----------------------------------------------
# (C)2005 mgr Jerzy Wałaszek
# I Liceum Ogólnokształcące
# im. K. Brodzińskiego
# w Tarnowie
#----------------------------------------------
print "Obliczanie wartosci dziesietnej"
print " dowolnej liczby binarnej"
print "==============================="
print "(C)2005 mgr Jerzy Walaszek"
print " I LO w Tarnowie"
print
print "Podaj liczbe binarna:"
print
bs = raw_input()
print
ds = "0"; i = 0
while (i < len(bs)) and ((bs[i] == "0") or (bs[i] == "1")):
p = 0 # Przeniesienie
c = ord(bs[i]) - 48 # Cyfra binarna
for j in range(len(ds) - 1, -1, -1):
# Schemat Hornera
s = 2 * (ord(ds[j]) - 48) + c + p
c = 0
# Wyznaczamy przeniesienie do następnej kolumny
p = s // 10
# Cyfrę wynikową zapisujemy w miejscu docelowym
ds = ds[:j] + chr((s % 10) + 48) + ds[j + 1:]
# Jeśli po wyczerpaniu cyfr ds przeniesienie p ma wartość
# większą od zera, to jest ono równe pierwszej cyfrze
if (j == 0) and (p > 0): ds = chr(p + 48) + ds
# Następna cyfra binarna
i += 1
print "Wartosc dziesietna liczby binarnej:"
print
print ds
print
raw_input("Nacisnij klawisz Enter...") |
| JavaScript | <html>
<head>
</head>
<body>
<div align="center">
<form style="BORDER-RIGHT: #ff9933 1px outset; PADDING-RIGHT: 4px;
BORDER-TOP: #ff9933 1px outset; PADDING-LEFT: 4px;
PADDING-BOTTOM: 1px; BORDER-LEFT: #ff9933 1px outset;
PADDING-TOP: 1px; BORDER-BOTTOM: #ff9933 1px outset;
BACKGROUND-COLOR: #ffcc66" name="frmbindec">
<h3 id="data_out" style="text-align: center">
Obliczanie wartości dziesiętnej<br>
dowolnej liczby binarnej</h3>
<p style="TEXT-ALIGN: center">
(C)2005 mgr Jerzy Wałaszek I LO w Tarnowie
</p>
<hr>
<div align="center">
<table border="0" cellpadding="4" style="border-collapse: collapse">
<tr>
<td align="center">Wprowadź poniżej liczbę binarną</td>
</tr>
<tr>
<td align="center">
<input value="111000111000111000111000111000111000111000111000"
name="inp_bs" size="80" style="text-align: right">
</td>
</tr>
<tr>
<td align="center">
<input onclick="main();" type="button"
value="Oblicz wartość dziesiętną" name="B1">
</td>
</tr>
</table>
</div>
<p id="out_t" style="TEXT-ALIGN: center">...</p>
</form>
<script language=javascript>
// Obliczanie wartości dowolnej liczby dwójkowej
//----------------------------------------------
// (C)2005 mgr Jerzy Wałaszek
// I Liceum Ogólnokształcące
// im. K. Brodzińskiego
// w Tarnowie
//----------------------------------------------
function main()
{
var bs,ds,i,j,c,p,s;
bs = document.frmbindec.inp_bs.value;
ds = "0"; i = 0;
while((i < bs.length) && ((bs.charAt(i) == '0') || (bs.charAt(i) == '1')))
{
p = 0; // Przeniesienie
c = bs.charCodeAt(i) - 48; // Cyfra binarna
for(j = ds.length - 1; j >= 0; j--)
{
// Schemat Hornera
s = 2 * (ds.charCodeAt(j) - 48) + c + p;
c = 0;
// Wyznaczamy przeniesienie do następnej kolumny
p = Math.floor(s / 10);
// Cyfrę wynikową zapisujemy w miejscu docelowym
ds = ds.substr(0,j) + String.fromCharCode((s % 10) + 48) +
ds.substring(j + 1,ds.length);
// Jeśli po wyczerpaniu cyfr ds przeniesienie p ma wartość
// większą od zera, to jest ono równe pierwszej cyfrze
if(!j && p) ds = String.fromCharCode(p + 48) + ds;
};
// Następna cyfra binarna
i++;
};
document.getElementById("out_t").innerHTML = ds;
}
</script>
</div>
</body>
</html> |
Dokument ten rozpowszechniany jest zgodnie z zasadami licencji
GNU Free Documentation License.
Źródło: mgr Jerzy Wałaszek
![]()
![]()
![]()
![]()
![]()
