Królewiec (obecnie Kaliningrad) leży nad rzeką Pregołą. Dzielnice leżące w jej pobliżu (z czego dwie leżące na wyspach śródrzecznych) łączyło w XVII wieku siedem mostów. Czy możliwe było takie ich przejście, by żaden z nich nie był „zaliczony” więcej niż raz?
 Królewiec (obecnie Kaliningrad) leży nad rzeką Pregołą. Dzielnice leżące w jej pobliżu (z czego dwie leżące na wyspach śródrzecznych) łączyło w XVII wieku siedem mostów. Czy możliwe było takie ich przejście, by żaden z nich nie był "zaliczony" więcej niż raz?
Królewiec (obecnie Kaliningrad) leży nad rzeką Pregołą. Dzielnice leżące w jej pobliżu (z czego dwie leżące na wyspach śródrzecznych) łączyło w XVII wieku siedem mostów. Czy możliwe było takie ich przejście, by żaden z nich nie był "zaliczony" więcej niż raz?
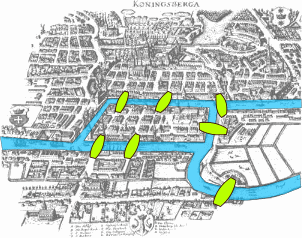
Nad tym problemem zastanawiał się słynny szwajcarski matematyk, Leonhard Euler. W dziele Solutio problematis ad geometriam situs pertinetis (skan w formacie .pdf) stwierdza, że przejście mostów w opisany wyżej sposób jest niemożliwe. Nie poprzestał jednak na tym- przeniósł problem na grunt teoretyczny, rozpatrując układ przepraw rzecznych jako swego rodzaju graf. Pytanie przybrało wówczas następującą postać: jakie warunki muszą być spełnione, żeby dany graf spójny można było opisać linią ciągłą w taki sposób, by każda krawędź tego grafu była obwiedziona tylko raz?
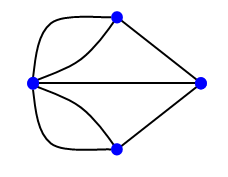
Powyższy rysunek przedstawia mosty królewieckie w formie grafu spójnego. Lewy wierzchołek to pierwsza wyspa, prawy- to druga wyspa, a wierzchołek górny i dolny reprezentują oba brzegi rzeki. Euler udowodnił, że takiego grafu nie można opisać linią ciągłą w sposób opisany wyżej. Dlaczego?
W lewym wierzchołku spotyka się pięć krawędzi. W prawym, górnym i dolnym- po trzy. W ten sposób uzyskujemy 4 wierzchołki, w których spotyka się nieparzysta liczba krawędzi. Tymczasem Euler pokazał, że takich wierzchołków musi być 0 lub 2, by graf (zwany wówczas eulerowskim) można było obwieść linią bez kilkukrotnego "zaliczania" poszczególnych krawędzi.
Te warunki spełnia graf, który powstałby po dobudowaniu jeszcze jednego, dwóch lub trzech mostów.
Ciekawostką jest, że obecna liczba mostów w Kaliningradzie (jest ich 5, z czego już tylko dwa pochodzą z czasów Eulera) pozwala na ich przejście zgodnie z warunkami założonymi przez Szwajcara. Jest to jednak wędrówka bardzo niepraktyczna dla turystów, ponieważ zaczynają podróż na jednej wyspie, a kończą na drugiej.
Zagadnienie mostów królewieckich wykorzystano także w mapie do gry komputerowej N, której główny bohater- ninja- musi, pokonując różne przeszkody, znaleźć drogę do wyjścia. Oczywiście w tym wypadku jest to niemożliwe.
Hymn teorii grafów
Na odbywającej się w 1981 w czechosłowackim Jabłońcu nad Nysą Konferencji z Teorii Grafów kilku prelegentów zaproponowało stworzenie hymnu, poświęconego teorii grafów. Wiosną 1982 prof. Bohdan Zelinka przygotował tekst, poświęcony głównie zagadnieniu mostów królewieckich, jako słynnemu problemowi rozwiązanemu z pomocą teorii grafów. Został on zaprezentowany światu w maju 1983, na odbywającej się w Zemplínskiej Šíravie Konferencji z Teorii Grafów. Bardzo szybko pojawiły się liczne tłumaczenia (polskie- autorstwa Mariusza Meszki and Joanny Nowak- zostało zaprezentowane w Krakowie w 1995 roku)- od angielskich po japońskie. Melodię hymnu (posłuchaj w formacie .mp3) przygotował Zdenek Ryjacek. Polski tekst hymnu:
1. Na Pregole siedem mostów stało, w tamtych czasach było to niemało. W Królewcu się radni radowali, że aż tyle mostów zbudowali.
2. Jak co wieczór tłumy wyruszyły, bo nad rzeką spacer bardzo miły. Wciąż myśl jedna im zaprząta głowę, jak tu wybrać tę właściwą drogę.
3. Przez most każdy raz przejść nie wracając, znów się w domu znaleźć nie zbaczając. Jakoś im to wcale nie wychodzi, most zostaje lub brakuje w drodze.
Ref. Eulera graf, to fakt oczywisty, wszystkie węzły są stopni parzystych. Doskonale znana jest o grafach to pierwsza z tez.
4. Aż nareszcie przypomnieli sobie o człowieku żyjącym w ich grodzie, Mistrzu geometrii i rachunków, On podpowie w którym iść kierunku.
5. Ale Euler smutnie kręci głową, bo odpowiedź na to ma gotową: “Jedna ścieżka nie wystarczy, aby pokryć mosty - nie ma na to rady.”
Ref. Eulera graf . . .
6. Nie pomogą tutaj dobre chęci, nic w nauce nie da się pokręcić. Mostów nowych nikt nie wybuduje, wodny żywioł tym co są – daruje.
7. Kiedy wojna przez Pregołę gnała, mosty wszystkie z ziemią wyrównała. Jednak imię Mistrza nad tą rzeką przeżyło już wiele długich wieków.
Ref. Eulera graf . . .
8. Nowej wiedzy Euler dał podstawy, przez co zyskał całe wieki sławy. My śladami Mistrza podążamy i naukę Jego rozwijamy.
9. Więc, Koledzy, na koniec powstańmy. Wznosząc toast głośno tak śpiewajmy: Niechaj żyje nam Teoria Grafów, obwieszczajmy ją całemu światu.
Tekst oryginalny, tłumaczenia (angielskie, niemieckie, polskie, węgierskie, afrikaans, esperanto, ukraińskie, indonezyjskie, francuskie) i nuty są dostępne w pliku .pdf (pochodzącym z strony Brief history of the Graph Theory Hymn, przygotowanej przez Zdenka Ryjacka).
Źródło: http://www.adamklimowski.tox.pl/zagadnienie-mostow-krolewieckich.html
Licencja: Creative Commons - użycie niekomercyjne - na tych samych warunkach
