JustPaste.it

Kod Gray'a

33e27ee6ebd8ba380dd2ab1927739cb6.gif

 

28bd12bba3e039502df3e0166d7fafeb.jpg

Wyobraźmy sobie, iż konstruujemy ramię robota. Ramię to ma zataczać kąt 32º (na potrzeby przykładu, w rzeczywistości może to być dowolny kąt). W przegubie ramienia umieszczamy czujnik, który odczytuje położenie ramienia i przekazuje kąt obrotu w postaci 5-bitowego naturalnego kodu binarnego.

00000 ---  0º
00001 ---  1º
00010 ---  2º

...

11110 --- 30º
11111 --- 31º

Na pierwszy rzut oka rozwiązanie to wydaje się całkiem sensowne. Mamy ramię. Mamy czujnik obrotu i mamy kod binarny, za pomocą którego czujnik przekazuje informację o położeniu tegoż ramienia. Dane te komputer sterujący może wykorzystywać do kierowania ruchami robota.

A teraz nadchodzi rzeczywistość. Bity z czujnika nie zmieniają się równocześnie - układ pomiarowy ma luzy. Z tego powodu w pewnych sytuacjach mogą pojawić się nieprawidłowe dane z czujnika. Na przykład wyobraźmy sobie, iż ramię obraca się z położenia 15º do położenia 16º:

01111(2) ---  15º - stan początkowy
11110(2) ---  31º - stan przejściowy, bity środkowe nie zdążyły się jeszcze zmienić
11010(2) ---  26º - stan przejściowy, jeszcze są bity niezmienione
10000(2) ---  16º - stan końcowy, ramię osiągnęło zadane położenie

Zwróć uwagę, iż w podanym przykładzie jeśli odczyt danych z czujnika nastąpi przed ustaleniem się stanów jego bitów (po zaniknięciu luzów w układzie pomiarowym), to odczytana wartość ma niewiele wspólnego z rzeczywistym położeniem ramienia robota. Jeśli program sterujący nie uwzględnia błędnych odczytów, może dojść do bardzo dziwnych rzeczy - np. ramię zacznie oscylować w jedną i w drugą stronę, ponieważ komputer sterujący sądzi, iż jest ono w innym położeniu niż powinno być.

Dlaczego tak się dzieje - po prostu zastosowaliśmy zły kod. Idealny kod pomiarowy powinien zmieniać tylko jeden bit przy przechodzeniu do następnej wartości - nasz zmienia tu wszystkie bity, stąd jeśli zmiana nie nastąpi synchronicznie, mogą pojawić się kłopoty. Taki kod istnieje i nosi nazwę kodu Gray'a.

67e2344444b1475661960748aaaf7f02.gif    
   
   

aca20fa685182821a6cc738278371258.gif

Kolejne wyrazy kodu Gray'a różnią się od siebie stanem tylko jednego bitu.

  
       

 

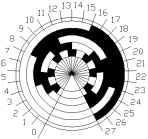
95e9963f753115572f351246f4340dcf.gif

Co nam to da? Bardzo dużo. Przy poprzednim kodzie niepewność odczytu mogła w niekorzystnych warunkach dotyczyć wszystkich bitów słowa kodowego. W przypadku kodu Gray'a niepewność ta dotyczy tylko 1 bitu, gdyż tylko jeden bit zmienia swój stan przy przejściu do następnego słowa kodowego. Zatem przykład może wyglądać następująco:

01000(GRAY) --- 15º - stan początkowy
01000(GRAY) --- 15º - stan pośredni, bity jeszcze się nie ustaliły
11000(GRAY) --- 16º - stan końcowy

W kodzie Gray'a słowa kodowe o wartości 15 (01000) i 16 (11000) różnią się tylko jednym bitem. Zatem nie dojdzie do dużych błędów odczytu położenia.

Gdy już wiemy do czego może służyć kod Gray'a (a zastosowań ma bardzo dużo), przejdziemy do sposobu konstrukcji poszczególnych wyrazów. Podana przez nas metoda tworzy tylko jeden z możliwych kodów Gray'a. Pozostałe uzyskuje się np. przez permutację bitów w słowach kodowych.

67e2344444b1475661960748aaaf7f02.gif    
   
    aca20fa685182821a6cc738278371258.gifWyznaczanie i-tego wyrazu n-bitowego kodu Gray'a
  1. Zapisujemy numer wyrazu kodu Gray'a w naturalnym kodzie dwójkowym na zadanej liczbie bitów. Brakujące bity uzupełniamy bitem 0.
  2. Pod spodem wypisujemy ten sam numer przesunięty w prawo o 1 bit. Najmniej znaczący bit odrzucamy. Na początku dopisujemy bit o wartości 0.
  3. Nad odpowiadającymi sobie bitami wykonujemy operację logiczną XOR. Wynik jest wyrazem w kodzie Gray'a.
 
       

 

1454a6e2b14594119bd02dd3870b73f5.gif

 

Dla przykładu znajdźmy za pomocą tej metody wszystkie 16 wyrazów 4 bitowego kodu Gray'a:

Wyraz 0  Kod dwójkowy 0000 0000
XOR 0000
0000		  Kod Gray'a 0000
Wyraz 1 Kod dwójkowy 0001 0001
XOR 0000
0001		  Kod Gray'a 0001
Wyraz 2 Kod dwójkowy 0010 0010
XOR 0001
0011		 Kod Gray'a 0011
Wyraz 3 Kod dwójkowy 0011 0011
XOR 0001
0010		 Kod Gray'a 0010
Wyraz 4 Kod dwójkowy 0100 0100
XOR 0010
0110		 Kod Gray'a 0110
Wyraz 5 Kod dwójkowy 0101 0101
XOR 0010
0111		 Kod Gray'a 0111
Wyraz 6 Kod dwójkowy 0110 0110
XOR 0011
0101		 Kod Gray'a 0101
Wyraz 7 Kod dwójkowy 0111 0111
XOR 0011
0100		 Kod Gray'a 0100
Wyraz 8 Kod dwójkowy 1000 1000
XOR 0100
1100		 Kod Gray'a 1100
Wyraz 9 Kod dwójkowy 1001 1001
XOR 0100
1101		 Kod Gray'a 1101
Wyraz 10 Kod dwójkowy 1010 1010
XOR 0101
1111		 Kod Gray'a 1111
Wyraz 11 Kod dwójkowy 1011 1011
XOR 0101
1110		 Kod Gray'a 1110
Wyraz 12 Kod dwójkowy 1100 1100
XOR 0110
1010		 Kod Gray'a 1010
Wyraz 13 Kod dwójkowy 1101 1101
XOR 0110
1011		 Kod Gray'a 1011
Wyraz 14 Kod dwójkowy 1110 1110
XOR 0111
1001		 Kod Gray'a 1001
Wyraz 15 Kod dwójkowy 1111 1111
XOR 0111
1000		 Kod Gray'a 1000

Zbierzmy otrzymane wyniki w tabeli. Kolorem czerwonym zaznaczyliśmy bity, które ulegają zmianie w stosunku do poprzedniego wyrazu.

Lp. Kod binarny Kod Gray'a
0  0000 0000
1 0001 0001
2 0010 0011
3 0011 0010
4 0100 0110
5 0101 0111
6 0110 0101
7 0111 0100
8 1000 1100
9 1001 1101
10 1010 1111
11 1011 1110
12 1100 1010
13 1101 1011
14 1110 1001
15 1111 1000

Zwróćcie uwagę, iż wyrazy kodu Gray'a tworzą zamknięty pierścień. Ostatni wyraz różni się od pierwszego również tylko jednym bitem. Tego typu kod nazywamy kodem Gray'a odzwierciedlonym binarnie (ang. binary reflected Gray code), ponieważ powstał przez proste przekształcenie kodu dwójkowego.

e5473c647673e460f19f8c79940bdf25.gif

Przekształcenie kodu dwójkowego w kod Gray'a, jak obserwowaliśmy w poprzednim paragrafie, jest dosyć proste. Równie mało skomplikowana jest operacja odwrotna.  Przeliczenia dokonujemy kopiując najstarszy bit kodu Gray'a do najstarszego bitu kodu binarnego. Pozostałe bity otrzymamy wykonując operację XOR na i-tym bicie kodu Gray'a i (i+1)-bicie wyrazu binarnego. Dla przykładu przeliczmy słowo w kodzie Gray'a 1110 na odpowiadające mu słowo dwójkowe:

Przeliczanie kodu Gray'a na naturalny kod dwójkowy
Operacja Opis
  1 1 1 0
         
  1 ? ? ?
Przepisujemy najstarszy bit z kodu Gray'a do najstarszego bitu słowa dwójkowego. Bity te w obu kodach mają tę samą wartość.
  1 1 1 0
XOR    1    
  1 0 ? ?
Otrzymany bit umieszczamy na pozycji przesuniętej w prawo o jedno miejsce i wykonujemy operację XOR z bitem kodu Gray'a. W ten sposób otrzymujemy kolejne bity kodu dwójkowego. W tym przypadku dostajemy bit o wartości 0.
  1 1 1 0
XOR      0  
  1 0 1 ?
Identyczną operację wykonujemy z poprzednio otrzymanym bitem o wartości 0 otrzymując bit kodu dwójkowego o wartości 1.
  1 1 1 0
XOR        1
  1 0 1 1
Ostatnia operacja daje w wyniku słowo binarne 1011, które posłużyło do utworzenia słowa kodu Gray'a o wartości 1110.

2a89bfb7bc9870300c343a39c14db16f.gif

Kod Gray'a jest kodem kombinatorycznym. Poszczególne pozycje bitów nie posiadają ustalonych wag, jak w przypadku opisanych poprzednio kodów binarnych. Wyrazy można tworzyć rekurencyjnie z wyrazów już wcześniej utworzonych wg następującego schematu:

67e2344444b1475661960748aaaf7f02.gif    
   
    aca20fa685182821a6cc738278371258.gifRekurencyjny n bitowy kod Gray'a powstaje w sposób następujący

Definiujemy działania na obiektach używanych przez algorytm:

  • Jeśli L jest listą wyrazów binarnych, to L jest listą tych wyrazów wziętych w odwrotnej kolejności.
    Na przykład
    L = {00,01,11,10}
    L = {10,11,01,00}     - kolejność odwrotna
  • b+L jest nową listą utworzoną przez dołączenie bitu b na początek wszystkich wyrazów listy L.
    Na przykład
    L = {00,01,11,10} - lista wyrazów 2-bitowych
    0+L = {000,001,011,010} - lista wyrazów 3-bitowych
    1+L = {100,101,111,110} - lista wyrazów 3-bitowych
  • L1 Å L2 jest listą powstałą przez złączenie tych dwóch list.
    Na przykład
    L1 = {000,001,011,010} - lista 4-elementowa
    L2 = {100,101,111,110} - lista 4-elementowa
    L1 Å L2 = {000,001,011,010,100,101,111,110} - lista 8-elementowa

Nowa lista wyrazów n-bitowego kodu Gray'a powstaje wg wzoru rekurencyjnego:

Dla n > 0

Jeśli n = 1, to LGRAY(1) = {0,1}
inaczej LGRAY(n) = 0 + LGRAY(n-1) Å  1 + LGRAY(n-1)

  
       

Wynika z tego, iż nowa lista wyrazów kodu Gray'a powstaje z poprzedniej listy po dodaniu na początku wszystkich wyrazów bitu 0 oraz dołączeniu tej samej poprzedniej listy z odwróconą kolejnością wyrazów i dodanym na początku bitem 1. Poniższy przykład pokaże nam, jak to się odbywa.

1454a6e2b14594119bd02dd3870b73f5.gif

 

Utworzymy 4-bitowy kod Gray'a wg opisanej metody rekurencyjnej. Jednakże pójdziemy od dołu do góry, tworząc coraz dłuższe kody wynikowe. Rozpoczynamy od n=1. Dla tego przypadku metoda tworzy listę bezpośrednią:

LGRAY(1) = {0,1}

Teraz tworzymy listę wyrazów kodu Gray'a dla n=2 wykorzystując listę utworzoną dla n=1. Wyrazy tej listy zaznaczyliśmy kolorem czerwonym.

LGRAY(2) = 0 + LGRAY(1) Å  1 + LGRAY(1)

0 + LGRAY(1) = {00,01}
1 + LGRAY(1) = {11,10}

LGRAY(2) = {00,01} Å  {11,10}
LGRAY(2) = {00,01,11,10}

Wyznaczamy listę 3-bitowego kodu Gray'a na podstawie listy 2-bitowego kodu:

LGRAY(3) = 0 + LGRAY(2) Å  1 + LGRAY(2)

0 + LGRAY(2) = {000,001,011,010}
1 + LGRAY(2) = {110,111,101,100}

LGRAY(3) = {000,001,011,010} Å  {110,111,101,100}
LGRAY(3) = {000,001,011,010,110,111,101,100}

Podobnie postępujemy dla listy 4-bitowego kodu Gray'a:

LGRAY(4) = 0 + LGRAY(3) Å  1 + LGRAY(3)

0 + LGRAY(3) = {0000,0001,0011,0010,0110,0111,0101,0100}
1 + LGRAY(3) = {1100,1101,1111,1110,1010,1011,1001,1000}

LGRAY(4) = {0000,0001,0011,0010,0110,0111,0101,0100} Å  {1100,1101,1111,1110,1010,1011,1001,1000}
LGRAY(4) = {0000,0001,0011,0010,0110,0111,0101,0100,1100,1101,1111,1110,1010,1011,1001,1000}

40e9a0b70c30d784b4d598d244ac21ba.gif

67e2344444b1475661960748aaaf7f02.gif    
   
   

f10ad766c7936434a9e503ebff44ae5f.gif

Poniższe, przykładowe programy są praktyczną realizacją omawianego w tym rozdziale algorytmu. Zapewne można je napisać bardziej efektywnie. To już twoje zadanie. Dokładny opis stosowanych środowisk programowania znajdziesz we wstępie. Programy przed opublikowaniem w serwisie edukacyjnym zostały dokładnie przetestowane. Jeśli jednak znajdziesz jakąś usterkę (co zawsze może się zdarzyć), to prześlij o niej informację do autora. Pozwoli to ulepszyć nasze artykuły. Będziemy Ci za to wdzięczni.

  
       

Program pracuje wg powyższego algorytmu rekurencyjnego tworząc kody Gray'a. Oczywiście zastosowaliśmy kilka usprawnień, których znalezienie i rozpracowanie pozostawiamy ambitnym czytelnikom.

Wydruk z uruchomionego programu 
Generacja kodu Gray'a
---------------------
(C)2005 J.Wałaszek
      I LO w Tarnowie

Ile bitów (1..16) ? 3

000
001
011
010
110
111
101
100

KONIEC. Naciśnij dowolny klawisz...
Microsoft Visual Basic 2005 Express Edition

 

 

 

Borland
Delphi 7.0
Personal
Edition		 
// Generowanie wszystkich wyrazów kodu Graya
//         o zadanej liczbie bitów
//------------------------------------------
// (C)2005 mgr Jerzy Wałaszek
//                 I Liceum Ogólnokształcące
//                 im. K. Brodzińskiego
//                 w Tarnowie
//------------------------------------------

program KodGraya;

{$APPTYPE CONSOLE}

// W tablicy WyrazyGraya tworzone będą kolejne
// wyrazy kodowe. Tablica ta musi posiadać tyle
// elementów, ile jest wszystkich wyrazów kodu.

var
  WyrazyGraya : array[0..65535] of word;

// Funkcja oblicza potęgę liczby 2
//--------------------------------
function Pot2(n : cardinal) : cardinal;
var
  p : cardinal;
begin
  p := 1;
  while n > 0 do
  begin
    p := p + p;
    dec(n);
  end;
  Pot2 := p;
end;

// Rekurencyjna procedura generacji wyrazów kodu Graya
//----------------------------------------------------
procedure Gray(n : cardinal);
var
  i,p : cardinal;
begin
  if n = 1 then
  begin
    WyrazyGraya[0] := 0;
    WyrazyGraya[1] := 1;
  end
  else
  begin
    Gray(n - 1); // wyznaczamy poprzednie wyrazy
    p := Pot2(n - 1);
    for i := p  to p + p - 1 do
      WyrazyGraya[i] := p + WyrazyGraya[p + p - i - 1];
  end;
end;

// Procedura wyświetlająca zawartość tablicy WyrazyGraya
//------------------------------------------------------
procedure Pisz(n : cardinal);
var
  i,j,kg : cardinal;
  s      : string;
begin
  for i := 0 to Pot2(n) - 1 do
  begin
    s  := '';
    kg := WyrazyGraya[i];
    for j := 1 to n do
    begin
      s  := char(48 + kg mod 2) + s;
      kg := kg div 2;
    end;
    writeln(s);
  end;
end;

var
  n : cardinal;
begin
  writeln('Generacja kodu Gray''a');
  writeln('---------------------');
  writeln('(C)2005 J.Walaszek');
  writeln('      I LO w Tarnowie');
  writeln;
  write('Ile bitow (1..16) ? '); readln(n);
  writeln;
  if not(n in [1..16]) then
    writeln('Niepoprawna liczba bitow n!')
  else
  begin
    Gray(n); Pisz(n);
  end;
  writeln;
  write('Nacisnij klawisz Enter...'); readln;
end.
Borland
C++ Builder
6.0
Personal
Edition		 
// Generowanie wszystkich wyrazów kodu Graya
//         o zadanej liczbie bitów
//------------------------------------------
// (C)2005 mgr Jerzy Wałaszek
//                 I Liceum Ogólnokształcące
//                 im. K. Brodzińskiego
//                 w Tarnowie
//------------------------------------------

#include <iostream>
#include <string>

using namespace std;

// W tablicy WyrazyGraya tworzone będą kolejne
// wyrazy kodowe. Tablica ta musi posiadać tyle
// elementów, ile jest wszystkich wyrazów kodu.

unsigned WyrazyGraya[65536];

// Funkcja oblicza potęgę liczby 2
//--------------------------------
unsigned Pot2(unsigned n)
{
  unsigned p;

  p = 1;
  while(n-- > 0) p += p;
  return(p);
}

// Rekurencyjna procedura generacji wyrazów kodu Graya
//----------------------------------------------------
void Gray(unsigned n)
{
  unsigned i, p;

  if(n == 1)
  {
    WyrazyGraya[0] = 0;
    WyrazyGraya[1] = 1;
  }
  else
  {
    Gray(n - 1); // wyznaczamy poprzednie wyrazy
    p = Pot2(n - 1);
    for(i = p; i < p + p; i ++)
      WyrazyGraya[i] = p + WyrazyGraya[p + p - i - 1];
  };
}

// Procedura wyświetlająca zawartość tablicy WyrazyGraya
//------------------------------------------------------
void Pisz(unsigned n)
{
  unsigned i, j, kg, p;
  string s;

  p = Pot2(n);
  for(i = 0; i < p; i++)
  {
    s  = "";
    kg = WyrazyGraya[i];
    for(j = 1; j <= n; j++)
    {
      s  = (char)(48 + kg % 2) + s;
      kg /= 2;
    };
    cout << s << endl;
  };
}

main()
{
  unsigned n;
  char z[1];

  cout << "Generacja kodu Gray'a\n"
          "---------------------\n"
          "(C)2005 J.Walaszek\n"
          "      I LO w Tarnowie\n\n"
          "Ile bitow (1..16) ? ";
  cin >> n;
  cout << endl;
  if((n < 1) || (n > 16))
    cout << "Niepoprawna liczba bitow n!";
  else
  {
    Gray(n); Pisz(n);
  };
  cout << "\n\nNacisnij ENTER...\n";
  cin.getline(z,1);
  cin.getline(z,1);
}
Microsoft
Visual
Basic 2005
Express
Edition		 
' Generowanie wszystkich wyrazów kodu Graya
'         o zadanej liczbie bitów
'------------------------------------------
' (C)2005 mgr Jerzy Wałaszek
'                 I Liceum Ogólnokształcące
'                 im. K. Brodzińskiego
'                 w Tarnowie
'------------------------------------------

Option Explicit On

Module Module1

  ' W tablicy WyrazyGraya tworzone będą kolejne
  ' wyrazy kodowe. Tablica ta musi posiadać tyle
  ' elementów, ile jest wszystkich wyrazów kodu.

  Dim WyrazyGraya(65536) As UShort

  ' Funkcja oblicza potęgę liczby 2
  '--------------------------------
  Public Function Pot2(ByVal n As UInteger) As UInteger
    Dim p As UInteger

    p = 1
    While n > 0
      p = p + p : n = n - 1
    End While
    Return p
  End Function

  ' Rekurencyjna procedura generacji wyrazów kodu Graya
  '----------------------------------------------------
  Public Sub Gray(ByVal n As UInteger)
    Dim i, p As UInteger

    If n = 1 Then
      WyrazyGraya(0) = 0
      WyrazyGraya(1) = 1
    Else
      Gray(n - 1)  ' wyznaczamy poprzednie wyrazy
      p = Pot2(n - 1)
      For i = p To p + p - 1
        WyrazyGraya(i) = p + WyrazyGraya(p + p - i - 1)
      Next
    End If
  End Sub

  ' Procedura wyświetlająca zawartość tablicy WyrazyGraya
  '------------------------------------------------------
  Public Sub Pisz(ByVal n As UInteger)
    Dim i, j, kg As UInteger
    Dim s As String

    For i = 0 To Pot2(n) - 1
      s = ""
      kg = WyrazyGraya(i)
      For j = 1 To n
        s = Chr(48 + kg Mod 2) + s
        kg = kg \ 2
      Next
      Console.WriteLine(s)
    Next
  End Sub

  Sub Main()

    Dim n As UInteger

    Console.WriteLine("Generacja kodu Gray'a")
    Console.WriteLine("---------------------")
    Console.WriteLine("(C)2005 J.Wałaszek")
    Console.WriteLine("      I LO w Tarnowie")
    Console.WriteLine()
    Console.Write("Ile bitów (1..16) ? ") : n = Val(Console.ReadLine())
    Console.WriteLine()
    If (n < 1) Or (n > 16) Then
      Console.WriteLine("Niepoprawna liczba bitów n!")
    Else
      Gray(n) : Pisz(n)
    End If
    Console.WriteLine()
    Console.WriteLine("KONIEC. Naciśnij dowolny klawisz...")
    Console.ReadLine()

  End Sub

End Module
Python 
# -*- coding: cp1250 -*-
# Generowanie wszystkich wyrazów kodu Graya
#         o zadanej liczbie bitów
#------------------------------------------
# (C)2005 mgr Jerzy Wałaszek
#                 I Liceum Ogólnokształcące
#                 im. K. Brodzińskiego
#                 w Tarnowie
#------------------------------------------

# W tablicy WyrazyGraya tworzone będą kolejne
# wyrazy kodowe. Tablica ta musi posiadać tyle
# elementów, ile jest wszystkich wyrazów kodu.

WyrazyGraya = range(65536)

# Funkcja oblicza potęgę liczby 2
#--------------------------------
def Pot2(n):
  p = 1
  while n:
    p *= 2
    n -= 1
  return p

# Rekurencyjna procedura generacji wyrazów kodu Graya
#----------------------------------------------------
def Gray(n):
  if n == 1:
    WyrazyGraya[0] = 0
    WyrazyGraya[1] = 1
  else:
    Gray(n - 1)  # wyznaczamy poprzednie wyrazy
    p = Pot2(n - 1)
    for i in range(p, 2 * p):
      WyrazyGraya[i] = p + WyrazyGraya[2 * p - i - 1]

# Procedura wyświetlająca zawartość tablicy WyrazyGraya
#------------------------------------------------------
def Pisz(n):
  for i in range(Pot2(n)):
    s  = ""
    kg = WyrazyGraya[i]
    for j in range(n):
      s  = chr(48 + kg % 2) + s
      kg //=  2
    print s

print "Generacja kodu Gray'a"
print "---------------------"
print "(C)2005 J.Walaszek"
print "      I LO w Tarnowie"
print
n = int(raw_input("Ile bitow (1..16) ? "))
print
if (n < 1) or (n > 16):
  print "Niepoprawna liczba bitow n!"
else:
  Gray(n); Pisz(n)
print
raw_input("Nacisnij klawisz Enter...")
JavaScript 
<html>
  <head>
  </head>
  <body>
    <div align="center">
<form style="BORDER-RIGHT: #ff9933 1px outset;
             PADDING-RIGHT: 4px;
             BORDER-TOP: #ff9933 1px outset;
             PADDING-LEFT: 4px;
             PADDING-BOTTOM: 1px;
             BORDER-LEFT: #ff9933 1px outset;
             PADDING-TOP: 1px;
             BORDER-BOTTOM: #ff9933 1px outset;
             BACKGROUND-COLOR: #ffcc66" name="frmkody">
  <h3 style="text-align: center">
    Rekurencyjne wyznaczanie wyrazów<br>
    n-bitowego kodu Gray'a
  </h3>
  <p style="TEXT-ALIGN: center">
    (C)2005 mgr Jerzy Wałaszek&nbsp;&nbsp; I LO w Tarnowie
  </p>
  <hr>
  <div align="center">
    <table border="0" cellpadding="4" style="border-collapse: collapse">
    <tr>
      <td align="right">Liczba bitów n (1...16) =</td>
      <td>
        <input value="4" name="inp_n" size="10" style="text-align: right">
      </td>
    </tr>
  </table>
  </div>
  <p style="TEXT-ALIGN: center">
    <input onclick="main();" type="button" value="Oblicz wyrazy kodu Gray'a"
           name="B13">
  </p>
  <p id="out_t" style="TEXT-ALIGN: center">...</p>
</form>

<script language="javascript">

// Generowanie wszystkich wyrazów kodu Graya
// o zadanej liczbie bitów
//------------------------------------------
// (C)2005 mgr Jerzy Wałaszek
// I Liceum Ogólnokształcące
// im. K. Brodzińskiego
// w Tarnowie
//------------------------------------------

// W tablicy WyrazyGraya tworzone będą kolejne
// wyrazy kodowe. Tablica ta musi posiadać tyle
// elementów, ile jest wszystkich wyrazów kodu.

var WyrazyGraya = new Array();

// Funkcja oblicza potęgę liczby 2
//--------------------------------
function Pot2(n)
{
  var p;

  p = 1;
  while(n-- > 0) p += p;
  return(p);
}

// Rekurencyjna procedura generacji wyrazów kodu Graya
//----------------------------------------------------
function Gray(n)
{
  var i,p;

  if(n == 1)
  {
    WyrazyGraya[0] = "0";
    WyrazyGraya[1] = "1";
  }
  else
  {
    Gray(n - 1); // wyznaczamy poprzednie wyrazy
    p = Pot2(n - 1);

// Uwaga - bardzo ważna jest kolejność tych pętli !!!

    for(i = p; i < p + p; i ++)
      WyrazyGraya[i] = "1" + WyrazyGraya[p + p - i - 1];

    for(i = 0; i < p; i++)
      WyrazyGraya[i] = "0" + WyrazyGraya[i]; 
  };
}

// Procedura wyświetlająca zawartość tablicy WyrazyGraya
//------------------------------------------------------
function Pisz(n)
{
  var i,p,t;

  t = "";
  p = Pot2(n);
  for(i = 0; i < p; i++) t += WyrazyGraya[i] + " ";
  document.getElementById("out_t").innerHTML = t;
}

function main()
{
  var n;

  n = parseInt(document.frmkody.inp_n.value);
  if(isNaN(n) || (n < 1) || (n > 16))
    document.getElementById("out_t").innerHTML =
       "<font color=Red><b>Niepoprawna ilość bitów</b></font>";
  else
  {
    Gray(n); Pisz(n);
  };
}

</script>
    </div>
  </body>
</html>



Dokument ten rozpowszechniany jest zgodnie z zasadami licencji

GNU Free Documentation License.

 

Źródło: mgr Jerzy Wałaszek

technologia programowanie