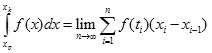Całkowanie numeryczne - wstęp

Całka jest jednym z najważniejszych pojęć współczesnej analizy matematycznej. Zastosowania ma tak liczne, iż trudno je wymienić. Stosuje się ją w matematyce, fizyce, technice i wielu innych dziedzinach nauki. W matematyce badaniem własności i obliczaniem wartości całek zajmuje się dział zwany rachunkiem całkowym. Za twórców tego rachunku uważa się dwóch wielkich matematyków Newtona oraz Leibniza, którzy opracowali teorię i metody związane z pojęciem całki i wprowadzili terminologię i oznaczenia zbliżone do stosowanych współcześnie, ukazujące związek rachunku całkowego z rachunkiem różniczkowym.

Nie wgłębiając się zbytnio w teorię matematyczną można powiedzieć, iż całką funkcji f(x) będzie każda funkcja F(x), której pochodna jest równa f(x), czyli F '(x) = f(x) Funkcję F(x) nazywamy funkcją pierwotną danej funkcji f(x). Funkcja pierwotna może być znaleziona z dokładnością do stałej, ponieważ stała znika w trakcie wyznaczania pochodnej. Funkcje pierwotne danej funkcji f(x) tworzą klasę funkcji różniących się stałymi: F(x) + C

 

Znajdźmy funkcję pierwotną od f(x) = 2x. Korzystamy ze znanego wzoru na pochodną funkcji:

F '(x) = 2x
ponieważ (axⁿ)' = anx^n-1
zatem F '(x) = (x² + C)' = 2x
stąd F(x) = x² + C

Funkcję pierwotną F(x) nazywamy całką nieoznaczoną funkcji f(x) i przedstawiamy symbolem wprowadzonym w 1689 roku przez matematyka niemieckiego G. W. Leibniza:

f(x)dx = F(x) + C

Zagadnienie obliczania całek nieoznaczonych sprowadza się do znajdowania postaci funkcji pierwotnej. Jest to dosyć skomplikowane i nie stanowi celu naszego opracowania. W całkowaniu numerycznym głównie zajmujemy się całkami oznaczonymi.

Całka oznaczona funkcji f(x) w przedziale <x_p,x_k> jest liczbą przedstawianą symbolem:

xk xp

f(x)dx

i obliczaną na różne sposoby. Przedział <x_p,x_k> nazywa się przedziałem całkowania. Krańce tego przedziału nazywa się granicami całkowania. x_p jest dolną granicą całkowania, a x_k górną granicą.

Jeśli znamy przepis na funkcję pierwotną F(x) funkcji podcałkowej f(x), to wartość całki oznaczonej funkcji f(x) w przedziale <x_p,x_k> możemy obliczyć w prosty sposób wg definicji Newtona-Leibniza:

xk xp

f(x)dx = F(xk) - F(xp)

Z punktu widzenia obliczeń komputerowych sposób ten nie jest najlepszy, ponieważ wymaga wyznaczenia funkcji pierwotnej F(x), co jest zadaniem numerycznie bardzo skomplikowanym - dopiero w ostatnich latach rozwiązano problem numerycznego wyznaczania wzoru całki dowolnej, całkowalnej funkcji w postaci analitycznej. Z metody tej korzystają zaawansowane pakiety matematyczne w stylu MathCAD.

Dużo większe zastosowanie w obliczeniach numerycznych ma definicja Riemanna, w której całka oznaczona jest interpretowana jako suma pól obszarów ograniczonych wykresem funkcji f(x) oraz osią OX. Obszary leżące pod osią mają w tej interpretacji pola ujemne.

Przedział całkowania <x_p,x_k> dzielimy na rozłączne podprzedziały wyznaczając n+1 punktów podziałowych:

x_p = x_o < x₁ < ... < x_n-1 < x_n = x_k

Punkty podziałowe muszą być tak dobrane, aby przy wzroście n do nieskończoności maksymalna odległość między sąsiednimi punktami malała do zera, czyli:

dla  i = 1, 2, ..., n

Pomiędzy parami sąsiednich punktów x_i-1 i x_i wybieramy dowolne punkty t_i spełniające nierówność:

dla  i = 1, 2, ..., n
x_i-1 < t_i < x_i

Całka oznaczona Riemanna jest wtedy granicą sum n prostokątów o podstawie równej (x_i - x_i-1) i wysokości f(t_i), czyli

Jeśli f(t_i) jest mniejsze od zera, to pole tego prostokąta zostanie zsumowane ze znakiem minus. Gdy odległości pomiędzy punktami podziałowymi zbliżają się do zera, suma pól prostokątów dąży do pola obszaru ograniczonego wykresem funkcji.

Różnicę pomiędzy wartością pola pod wykresem funkcji a polem otrzymanym jako suma skończonej ilości prostokątów nazywamy błędem całkowania. Wraz ze wzrostem liczby prostokątów w całce Riemanna błąd całkowania dąży do zera.

 

Dokument ten rozpowszechniany jest zgodnie z zasadami licencji
GNU Free Documentation License.

Źródło: mgr Jerzy Wałaszek