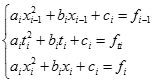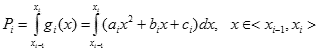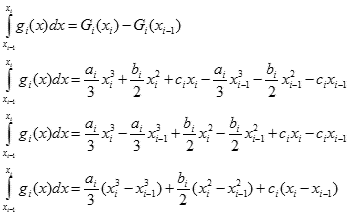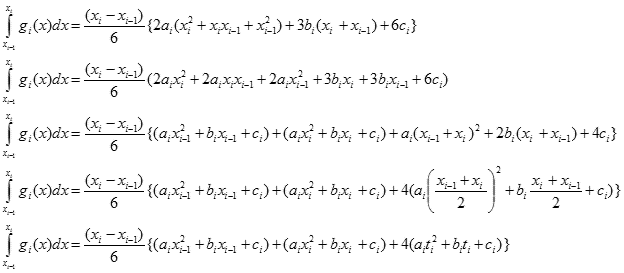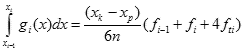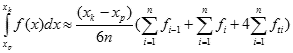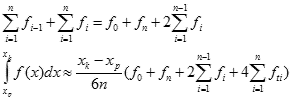| 
TRUDNE ! |
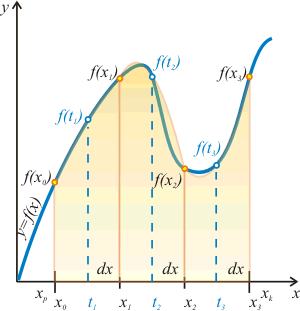
Metoda Simpsona jest najdokładniejszą z dotąd poznanych przez nas metod przybliżonego całkowania. W metodzie prostokątów całka oznaczona przybliżana była funkcjami stałymi - liczyliśmy sumę pól prostokątów. W metodzie trapezów całkę przybliżaliśmy za pomocą funkcji liniowych - obliczaliśmy sumy pól trapezów. W metodzie Simpsona stosujemy jako przybliżenie parabolę - będziemy obliczali sumy wycinków obszarów pod parabolą. Zasada jest następująca:
Przedział całkowania <xp,xk> dzielimy na n + 1 równo odległych punktów xo, x1, x2 ,..., xn:
dla i = 0,1,2,...,n
Dla każdych dwóch sąsiednich punktów wyznaczamy punkt środkowy ti wg wzoru:
dla i = 1,2,...,n
Obliczamy odległość między dwoma sąsiednimi punktami.
Dla każdego wyznaczonego w ten sposób punktu obliczamy wartość funkcji f(x) w tym punkcie:
| punkty podziałowe | punkty środkowe |
dla i = 0,1,2,...,n
fi = f(xi) | dla i = 1,2,...,n
fti = f(ti) |
W każdym podprzedziale <xi-1,xi> przybliżamy funkcję za pomocą paraboli g(x) o następującej postaci:
dla i = 1,2,...,n
gi(x) = aix2 + bix + ci, x  <xi-1, xi>
<xi-1, xi>
Parabola gi(x) musi przechodzić przez punkty: (xi-1,fi-1), (ti,fti), (xi,fi). Współczynniki ai, bi i ci wyznaczymy zatem z układu trzech równań:
dla i = 1,2,...,n
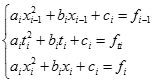
 | | |
| | |
| | |  W metodzie Simpsona chodzi o wyznaczenia pola pod parabolą w danym podprzedziale, a nie jej współczynników. Możemy zatem pójść inną drogą. Załóżmy, iż powyższe współczynniki są znane (ostatecznie możemy je przecież wyliczyć). | |
| | | | |
Pole pod parabolą w przedziale <xi-1,xi> będzie równe całce oznaczonej:
dla i = 1,2,...,n
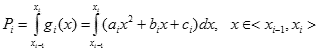
Funkcja pierwotna jest bardzo prosta w tym przypadku i ma wzór następujący:
dla i = 1,2,...,n
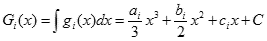
Wartość całki obliczymy zgodnie z definicją Newtona-Leibniza:
dla i = 1,2,...,n
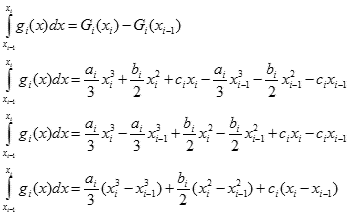
Teraz postaramy się uprościć maksymalnie otrzymane wyrażenie. W tym celu wyciągamy przed nawias wspólny czynnik i całość dzielimy przez 6:
dla i = 1,2,...,n
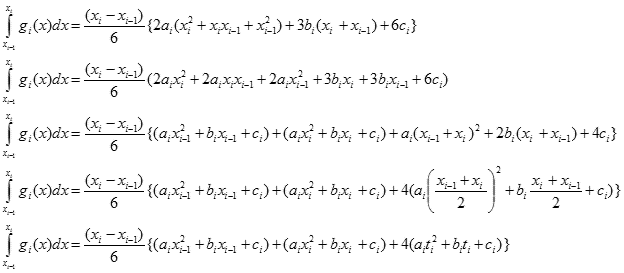
Zwróćcie uwagę, iż wyrażenia w nawiasach są odpowiednio wartościami funkcji fi-1, fi oraz fti. Natomiast różnica
xi - xi-1
jest odległością dx pomiędzy dwoma sąsiednimi punktami podziałowymi. Zatem po uproszczeniu otrzymujemy ostateczny wzór:
dla i = 1,2,...,n
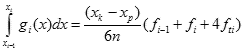
Wzór ten pozwala wyliczyć pole obszaru pod parabolą aproksymującą funkcję f(x) w przedziale <xi-1,xi>. Wartość całej całki otrzymamy sumując te pola, czyli:
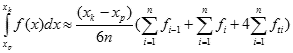
Jest to wzór wyliczania przybliżonej wartości całki oznaczonej za pomocą metody Simpsona. Ponieważ w obliczanych sumach wartości funkcji się powtarzają dwukrotnie (z wyjątkiem pierwszej i ostatniej), do obliczeń komputerowych stosujemy efektywniejszy wzór otrzymywania powyższej sumy:
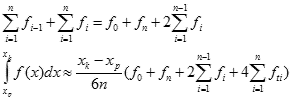

Dane wejściowe
| xp | - | początek przedziału całkowania, xp  R R |
| xk | - | koniec przedziału całkowania, xk  R R |
| n | - | liczba punktów podziałowych, n  N N |
| f(x) | - | funkcja rzeczywista, której całkę liczymy |
Dane wyjściowe
Wartość całki oznaczonej funkcji f(x) w przedziale <xp,xk>. Wynik jest liczbą rzeczywistą.
Zmienne pomocnicze
| s | - | suma wartości funkcji w punktach podziałowych, s  R R |
| st | - | suma wartości funkcji w punktach środkowych, st  R R |
| dx | - | odległość między dwoma sąsiednimi punktami podziałowymi, dx  R R |
| x | - | pozycja punktu podziałowego, x  R R |
| i | - | licznik punktów podziałowych, i  N N |

| krok 1: | Czytaj xp xk |
| krok 2: | s  0; st 0; st  0 0 |
| krok 3: | dx  | xk - xp | | n | |
| krok 4: | Dla i = 1,2,...,n, wykonuj kroki 5...7 |
| krok 5: | x 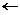 xp + i xp + i  dx dx |
| krok 6: | st  st + f(x - st + f(x - | dx | ) | | 2 | |
| krok 7: | Jeśli i < n, to s  s + f(x) s + f(x) |
| krok 8: | s  | dx |  (f(xp) + f(xk) + 2 (f(xp) + f(xk) + 2  s + 4 s + 4  st ) st ) | | 6 | |
| krok 9: | Pisz s i zakończ algorytm |

Odczytujemy krańce przedziału całkowania <xp,xk>. Do obliczenia całki metodą Simpsona musimy zliczyć dwie sumy - wartości funkcji w punktach podziałowych xi oraz wartości funkcji w punktach środkowych przedziałów ti. Pierwszą sumę będziemy obliczać w zmiennej s, drugą w st. Obie na początku przyjmują wartość 0. Wyznaczamy dalej odległość pomiędzy dwoma sąsiednimi punktami podziałowymi dx i rozpoczynamy pętlę, w której zmienna i pełni rolę numeru punktu podziałowego i środkowego. Pętla ta wykonuje się n-razy od i=1 do i=n włącznie, czyli jest to zwykła pętla iteracyjna typu FOR.
W pętli wyznaczamy wartość punktu podziałowego xi i umieszczamy ją w zmiennej x. Następnie obliczamy wartość funkcji w punkcie środkowym ti, który jest odległy o połowę dx od wyznaczonego wcześniej punktu xi. Wartość tę dodajemy do sumy st.
Drugą sumę tworzymy w zmiennej s. Jednakże powinna ona zawierać jedynie wartości funkcji dla punktów podziałowych od x1 do xn-1. Dlatego przed sumowaniem sprawdzamy, czy indeks i jest w odpowiednim zakresie.
Po zakończeniu pętli wyznaczamy wartość całki w zmiennej s zgodnie z podanym wzorem, wyprowadzamy ten wynik dla użytkownika i kończymy wykonywanie algorytmu.

 | | |
| | |
| | | 
Poniższe, przykładowe programy są praktyczną realizacją omawianego w tym rozdziale algorytmu. Zapewne można je napisać bardziej efektywnie. To już twoje zadanie. Dokładny opis stosowanych środowisk programowania znajdziesz we wstępie. Programy przed opublikowaniem w serwisie edukacyjnym zostały dokładnie przetestowane. Jeśli jednak znajdziesz jakąś usterkę (co zawsze może się zdarzyć), to prześlij o niej informację do autora. Pozwoli to ulepszyć nasze artykuły. Będziemy Ci za to wdzięczni. | |
| | | | |
W celu zobrazowania dokładności metody Simpsona zmniejszyliśmy w naszych przykładach liczbę punktów podziałowych do n=10. Wynik obliczenia całki jest niezmieniony w stosunku do metod prostokątów i trapezów. Zachęcamy do eksperymentów z liczbą N.
| Wydruk z uruchomionego programu |
Obliczanie całki oznaczonej
za pomocą metody Simpsona
----------------------------
(C)2006 mgr J.Wałaszek I LO
f(x) = x * x + 2 * x
Podaj początek przedziału całkowania
xp = 0
Podaj koniec przedziału całkowania
xk = 1
Wartość całki wynosi : 1,333
KONIEC. Naciśnij dowolny klawisz... |
| Microsoft Visual Basic 2005 Express Edition |
Borland
Delphi 7.0
Personal
Edition | //*************************************************
//** Obliczanie całki oznaczonej metodą Simpsona **
//** ------------------------------------------- **
//** (C)2004 mgr Jerzy Wałaszek I LO w Tarnowie **
//*************************************************
program int_simpson;
{$APPTYPE CONSOLE}
//*******************************
//** Tutaj definiujemy funkcję **
//*******************************
function f(x : real) : real;
begin
f := x * x + 2 * x;
end;
//********************
//** Program główny **
//********************
const N = 10; //liczba punktów podziałowych
var
xp,xk,s,st,dx,x : real;
i : integer;
begin
writeln('Obliczanie calki oznaczonej');
writeln(' za pomoca metody Simpsona');
writeln('---------------------------');
writeln('(C)2004 mgr J.Walaszek I LO');
writeln;
writeln('f(x) = x * x + 2 * x');
writeln;
writeln('Podaj poczatek przedzialu calkowania');
writeln;
write('xp = '); readln(xp);
writeln;
writeln('Podaj koniec przedzialu calkowania');
writeln;
write('xk = '); readln(xk);
writeln;
s := 0; st := 0;
dx := (xk - xp) / N;
for i := 1 to N do
begin
x := xp + i * dx;
st := st + f(x - dx / 2);
if i < N then s := s + f(x);
end;
s := dx / 6 * (f(xp) + f(xk) + 2 * s + 4 * st);
writeln('Wartosc calki wynosi : ',s:8:3);
writeln;
writeln('Nacisnij klawisz Enter...');
readln;
end. |
Borland
C++ Builder
6.0
Personal
Edition | //*************************************************
//** Obliczanie całki oznaczonej metodą Simpsona **
//** ------------------------------------------- **
//** (C)2004 mgr Jerzy Wałaszek I LO w Tarnowie **
//*************************************************
#include <iomanip>
#include <iostream>
using namespace std;
//*******************************
//** Tutaj definiujemy funkcję **
//*******************************
double f(double x)
{
return(x * x + 2 * x);
}
//********************
//** Program główny **
//********************
main()
{
const int N = 10; //liczba punktów podziałowych
double xp,xk,s,st,dx,x;
int i;
char c[1];
cout.precision(3); // 3 cyfry po przecinku
cout.setf(ios::fixed); // format stałoprzecinkowy
cout << "Obliczanie calki oznaczonej\n"
" za pomoca metody Simpsona\n"
"---------------------------\n"
"(C)2004 mgr J.Walaszek I LO\n\n"
"f(x) = x * x + 2 * x\n\n"
"Podaj poczatek przedzialu calkowania\n\n"
"xp = ";
cin >> xp;
cout << "\nPodaj koniec przedzialu calkowania\n\n"
"xk = ";
cin >> xk;
cout << endl;
s = 0; st = 0;
dx = (xk - xp) / N;
for(i = 1; i <= N; i++)
{
x = xp + i * dx;
st += f(x - dx / 2);
if(i < N) s += f(x);
}
s = dx / 6 * (f(xp) + f(xk) + 2 * s + 4 * st);
cout << "Wartosc calki wynosi : " << setw(8) << s
<< "\n\nNacisnij klawisz Enter";
cin.getline(c, 1);
cin.getline(c, 1);
} |
Microsoft
Visual
Basic 2005
Express
Edition | '*************************************************
'** Obliczanie całki oznaczonej metodą Simpsona **
'** ------------------------------------------- **
'** (C)2006 mgr Jerzy Wałaszek I LO w Tarnowie **
'*************************************************
Module Module1
'*******************************
'** Tutaj definiujemy funkcję **
'*******************************
Public Function f(ByVal x As Double) As Double
Return x * x + 2 * x
End Function
'********************
'** Program główny **
'********************
Sub Main()
Const N = 10 'liczba punktów podziałowych
Dim xp, xk, s, st, dx, x As Double
Dim i As Integer
Console.WriteLine("Obliczanie całki oznaczonej")
Console.WriteLine(" za pomocą metody Simpsona")
Console.WriteLine("----------------------------")
Console.WriteLine("(C)2006 mgr J.Wałaszek I LO")
Console.WriteLine()
Console.WriteLine("f(x) = x * x + 2 * x")
Console.WriteLine()
Console.WriteLine("Podaj początek przedziału całkowania")
Console.WriteLine()
Console.Write("xp = ") : xp = Val(Console.ReadLine())
Console.WriteLine()
Console.WriteLine("Podaj koniec przedziału całkowania")
Console.WriteLine()
Console.Write("xk = ") : xk = Val(Console.ReadLine())
Console.WriteLine()
s = 0 : st = 0
dx = (xk - xp) / N
For i = 1 To N
x = xp + i * dx
st += f(x - dx / 2)
If i < N Then s += f(x)
Next
s = dx / 6 * (f(xp) + f(xk) + 2 * s + 4 * st)
Console.WriteLine("Wartość całki wynosi : {0,8:F3}", s)
' Gotowe
Console.WriteLine()
Console.WriteLine("KONIEC. Naciśnij dowolny klawisz...")
Console.ReadLine()
End Sub
End Module |
| Python | # -*- coding: cp1250 -*-
#*************************************************
#** Obliczanie całki oznaczonej metodą Simpsona **
#** ------------------------------------------- **
#** (C)2005 mgr Jerzy Wałaszek I LO w Tarnowie **
#*************************************************
#*******************************
#** Tutaj definiujemy funkcję **
#*******************************
def f(x):
return x * x + 2 * x;
#********************
#** Program główny **
#********************
N = 10 #liczba punktów podziałowych
print "Obliczanie calki oznaczonej"
print " za pomoca metody Simpsona"
print "---------------------------"
print "(C)2005 mgr J.Walaszek I LO"
print
print "f(x) = x * x + 2 * x"
print
print "Podaj poczatek przedzialu calkowania"
print
xp = float(raw_input("xp = "))
print
print "Podaj koniec przedzialu calkowania"
print
xk = float(raw_input("xk = "))
print
s = st = 0.
dx = (xk - xp) / N
for i in range(1, N + 1):
x = xp + i * dx
st += f(x - dx / 2)
if i < N:
s += f(x)
s = dx / 6 * (f(xp) + f(xk) + 2 * s + 4 * st)
print "Wartosc calki wynosi : %8.3f" % s
print
raw_input("Koniec - nacisnij klawisz Enter...") |
| JavaScript | <html>
<head>
<title>Całkowanie numeryczne metodą Simpsona</title>
</head>
<body>
<script language="JavaScript">
//*************************************************
//** Obliczanie całki oznaczonej metodą Simpsona **
//** ------------------------------------------- **
//** (C)2004 mgr Jerzy Wałaszek I LO w Tarnowie **
//*************************************************
//*******************************
//** Tutaj definiujemy funkcję **
//*******************************
function f(x)
{
return(x * x + 2 * x);
}
function js_simpson()
{
var N = 10; //liczba punktów podziałowych
var xp,xk,s,st,dx,x,i,t;
xp = parseFloat(document.frm_simpson.xp_inp.value);
xk = parseFloat(document.frm_simpson.xk_inp.value);
if(isNaN(xp) || isNaN(xk))
t = "<font color=red><b>Popraw dane wejściowe!</b></font>";
else
{
s = 0; st = 0;
dx = (xk - xp) / N;
for(i = 1; i <= N; i++)
{
x = xp + i * dx;
st += f(x - dx / 2);
if(i < N) s += f(x);
};
s = dx / 6 * (f(xp) + f(xk) + 2 * s + 4 * st);
t = Math.floor(s * 1000) / 1000;
};
document.getElementById("t_out").innerHTML = t;
}
</script>
<form method="POST"
name="frm_simpson"
style="border: 2px solid #FF9900;
padding-left: 4px;
padding-right: 4px;
padding-top: 1px;
padding-bottom: 1px;
background-color: #FFFFCC">
<h2 style="text-align: center">
Obliczanie całki oznaczonej<br>
za pomocą metody Simpsona
</h2>
<hr>
<h4 style="text-align: center">
(C)2004 mgr Jerzy Wałaszek I LO w Tarnowie
</h4>
<h3 style="text-align: center">
Całkowana funkcja:
</h3>
<h4 style="text-align: center">
<i>f(x) = x<sup>2</sup> + 2x</i>
</h4>
<p style="text-align: center">
Tutaj określ przedział całkowania
</p>
<p style="text-align: center">
Początek <i>x<sub>p</sub></i> =
<input type="text" name="xp_inp" size="20" value="0">
i koniec <i>x<sub>k</sub> </i>=
<input type="text" name="xk_inp" size="20" value="1">
</p>
<p style="text-align: center">
<input onclick="js_simpson();" type="button"
value="Oblicz całkę" name="B1">
</p>
<h4 style="text-align: center">
Wartość całki wynosi
</h4>
<p id="t_out" style="text-align: center">...</p>
</form>
</body>
</html>
Dokument ten rozpowszechniany jest zgodnie z zasadami licencji
GNU Free Documentation License.
|
Źródło: mgr Jerzy Wałaszek

<xi-1, xi>
R
R
N
R
R
R
R
N
0; st
0
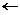
xp + i
dx
st + f(x -
s + f(x)
(f(xp) + f(xk) + 2
s + 4
st )