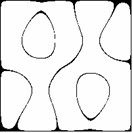
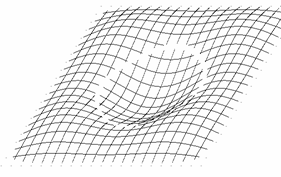
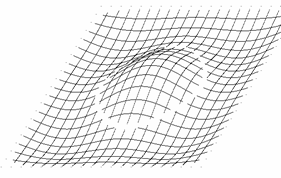
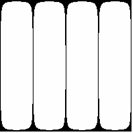
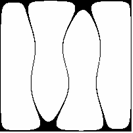
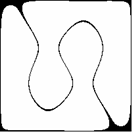
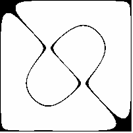
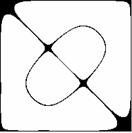
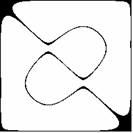
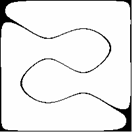
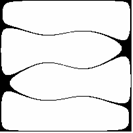
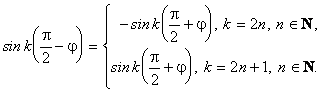Własności geometryczne figur Chladniego - symetrie płaskie i przestrzenne

Już pobieżna analiza wzorów (2.2), (2.3), (2.4) i (2.5) przekonuje nas, że przedstawione dotąd figury wykazują pewne symetrie. Udowodnimy na początku, że wszystkie figury (2.1) w rozpatrywanym układzie współrzędnych są środkowo symetryczne (środek układu jest środkiem symetrii, czyli punktem stałym przekształcenia). W tym celu wystarczy wykazać:

f(x,y) = f(-x,-y).

(3.1)

Aby dowieść równości (3.1) należy udowodnić tożsamość:

Dowód przeprowadzamy przenosząc wyrażenia na jedną stronę i stosując wzory na sumę i różnicę sinusów. Posługując się powyższym wzorem i rozpatrując parzyste i nieparzyste m, n dowodzimy słuszności równości (3.1).

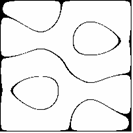
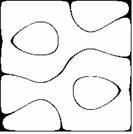
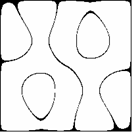
Z kursu geometrii szkoły średniej wiadomo, że symetria środkowa jest złożeniem dwóch symetrii osiowych o prostych prostopadłych. Dla niektórych z pokazanych już figur takimi prostymi mogą być osie układu współrzędnych (Rys. 2c,d, p. także Rys. 3a,b), np. dla m = 3, n = 1 f(x,y) = f(-x,-y) = 0 oraz f(x,y) = f(x,-y) = 0, a np. dla m = 3, n = 2 osie układu nie są osiami symetrii (Rys. 2f, p. także Rys. 4a,b). Ciekawe symetrie można również uzyskać pozostając przy tych samych wartościach m,n lub m,n, ale zmieniając parametr a (Rys.9a-d).

Rys. 9

a)

2 : 5; p/6
b)

2 : 5; -p/6

c)

5 : 2; p/6
d)

5 : 2; -p/6

Przy odwzorowaniu przestrzennym sytuacja jest nieco inna. Mamy tutaj do czynienia nie z liniami funkcyjnymi, ale z powierzchniami funkcyjnymi rozpiętymi nad obszarem zmienności funkcji (1.3). Aby taka figura przestrzenna była środkowo symetryczna musi być spełniony warunek:

f(x,y) = -f(-x,-y)

Symetria względem środka przestrzennego układu współrzędnych (punkt O) jest złożeniem trzech symetrii płaszczyznowych względem płaszczyzn xy, xz, yz parami prostopadłych, które mają punkt wspólny O [5]. Natomiast żadna z tych płaszczyzn nie jest płaszczyzną symetrii (mówimy też o antysymetrii) figury, tzn.

f(x,y) ≠ f(-x,y) ≠ f(x,-y) ≠ -f(x,y),

Możemy zaobserwować także inne ciekawe własności omawianych powierzchni funkcyjnych, np. zmieniając wartość parametru a na p + a uzyskujemy zwierciadlane odbicie w płaszczyźnie xy (Rys. 10a,b).

Rys. 10

a)

3 : 1; p/4
b)

3 : 1; 5p/4

Jeżeli w równaniu krzywych oprócz współrzędnych bieżących x i y występuje jeden lub kilka parametrów, to zbiór wszystkich krzywych nazywa się jedno- lub wieloparametrową rodziną krzywych, a równanie tych krzywych - równaniem rodziny [6].

Rozpatrzmy taką rodzinę dla m = 4, n = 1. Wówczas dla a Î <0,p/2> (Rys. 11a-i) równanie (1.2) przedstawia jednoparametrową rodzinę krzywych, ponieważ sina i cos a są związane tożsamościowo (jedynka trygonometryczna).

Rys. 11

a)

1 : 4; p/2
b)

1 : 4; 5p/12
c)

1 : 4; p/3

d)

1 : 4; 0,82
e)

1 : 4; p/4
f)

1 : 4; 0,74

g)

1 : 4; p/6
h)

1 : 4; p/12
i)

1 : 4; 0

Nietrudno zauważyć, że przy odpowiednio małym kroku zmian parametru a następuje w miarę płynne przejście jednej figury w drugą. Takie przekształcenie płaszczyzny można uznać jako namiastkę modnej ostatnio w grafice komputerowej metamorfozy, tzw. morfingu.

Jednocześnie na nasze przekształcenie możemy popatrzeć jak na obrót dookoła początku układu o kąt a = -p/4. Chociaż rezultat obydwu przekształceń jest taki sam, nie można doszukiwać się analogii między nimi. Obrót zawsze można sprowadzić do przekształcenia liniowego, a zaprezentowaną na Rys. 11 transformację - nie [7].

Dokument ten rozpowszechniany jest zgodnie z zasadami licencji
GNU Free Documentation License.