Krzywe algebraiczne - krzywa inwersji

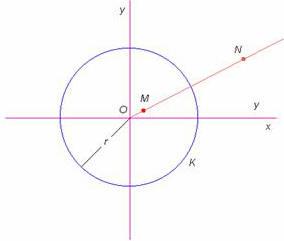
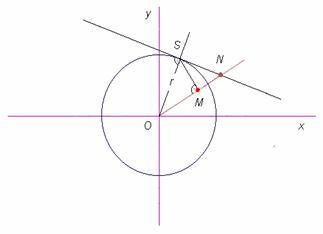
Inwersja względem okręgu K o środku O – przekształcenie geometryczne (inwolucja), które każdemu punktowi M leżącemu na półprostej wychodzącej z punktu O (różnemu od O) przyporządkowuje taki punkt N na tej półprostej, że OM ∙ ON = r², gdzie r jest promieniem okręgu. Mówimy, ze punkty M i N są symetryczne względem okręgu, zaś środek okręgu K jest środkiem inwersji. Inwersja przekształca punkty wewnętrzne okręgu K na punkty zewnętrzne i na odwrót.

Rys. I
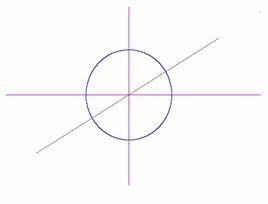
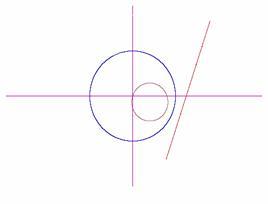
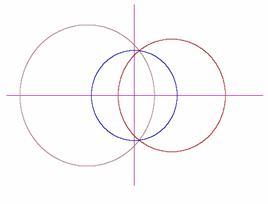
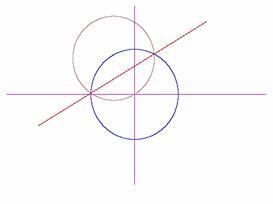
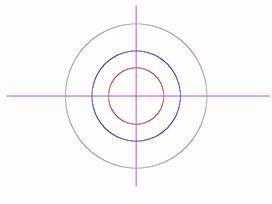
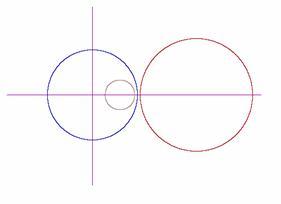
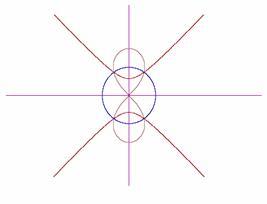
Przy inwersji prosta przechodząca przez środek okręgu inwersji przechodzi w tę samą prostą (Rys. 2.1), a prosta nie przechodząca przez środek inwersji - w okrąg (Rys. 2.2 i 2.3). Natomiast obrazem dowolnego okręgu jest inny okrąg (Rys. 2.4, 2.5, 2.6).
Inwersja należy do przekształceń geometrycznych zwanych inwolucją, przy którym punkt N jest obrazem punktu M, jeżeli punkt M jest obrazem punktu N. Przy dwukrotnym zastosowaniu inwolucji otrzymujemy przekształcenie tożsamościowe. Inne przykłady inwolucji to symetrie (osiowa, środkowa) [2].
    REM INWERSJA WZGLĘDEM OKREGU

    DEF FNx (t): DEF FNy (t)

    REM OKRĘG INWERSJI

    r = 100

    FOR t = -π TO π krok
      PSET (r*SIN(t),r*COS(t)),kolor
    NEXT t

10  FOR t = a TO b krok
      PSET (FNx(t), FNy(t)), kolor
    NEXT t

100 FOR t = a TO b krok
      x = FNx(t): y = FNy(t)
      MO = SQR(x^2+y^2)
      NO = r^2/MO
      PSET (NO*x/MO,NO*y/MO),kolor
    NEXT t
KOMENTARZ ALGORYTMU
Wszystkie występujące w programie pętle oczywiście mogą być zapisane jako jedna; uzyskujemy wówczas oszczędności czasowe, czyli jak mawiają informatycy, algorytm (program) jest bardziej sprawny. W niniejszej pracy nie jest to jednak istotne. Proponowany zapis ma natomiast pewne walory dydaktyczne. Po każdej pętli program może być zatrzymany (SLEEP, PAUSE, STOP) i użytkownik może prześledzić jego działanie krok po kroku.

Takie ujecie będzie stosowane również w programach poniżej.

W tym programie środek okręgu inwersji zajmuje stałe położenie i znajduje się w początku układu współrzędnych O(0,0). Jeżeli umieścimy go w dowolnym punkcie (x_o,y_o), kładziemy w pętli 10:
PSET (r*SIN(t)+x0),r*COS(t)+y0),kolor
Rys. 2.1

Rys. 2.3

Rys. 2.5

Rys. 2.2

Rys. 2.4

Rys. 2.6

Pytanie do użytkownika: Jak będzie wyglądał obraz okręgu stycznego wewnętrznie lub zewnętrznie do okręgu inwersji?

Rys. 2.7

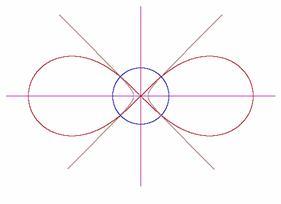
Hiperbola równoosiowa: x² - y² = a².
Rys. 2.8

Hiperbola jest krzywą inwersji dla lemniskaty.

Krzywa inwersji dla hiperboli jest lemniskatą, a dla lemniskaty – hiperbolą, gdy środek inwersji znajduje się w początku układu współrzędnych.

Rys. 2.9

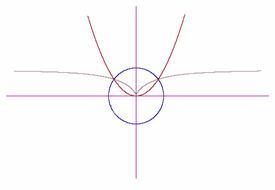
Cisoida Dioklesa, centrum inwersji –
wierzchołek paraboli.

Parabola typu y = ax² , a > 0
Rys. 2.10

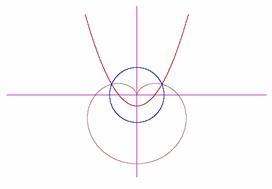
Kardioida, gdy centrum inwersji znajduje się
w ognisku paraboli.

Parabola typu: y = ax² + c, a > 0, c < 0.

Rys. 2.11

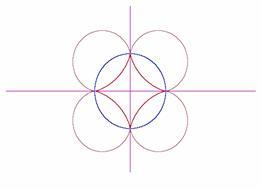
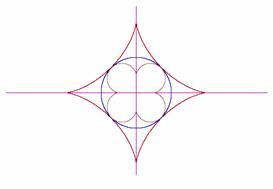
Okręgiem inwersji jest okrąg opisany
na astroidzie.
Rys. 2.12

Okrąg inwersji wpisany w astroidę.

W obydwu przypadkach uzyskujemy krzywe podobne do rozet czterolistnych. Czy istnieje przekształcenie przeprowadzające jedną w drugą?

Rys. II

Sposób konstrukcji punktów inwersji ma związek ze styczną do krzywej; punkty położone na okręgu są punktami stałymi przekształcenia, punkty M i N nazywa się też punktami symetrycznymi względem okręgu.

Linie stowarzyszone z krzywymi, o których będziemy mówić w następnym rozdziale mają związek ze styczną do linii.

Dokument ten rozpowszechniany jest zgodnie z zasadami licencji
GNU Free Documentation License.

Źródło: mgr Tadeusz Sypek

technologia programowanie