Krzywe algebraiczne - antypodera

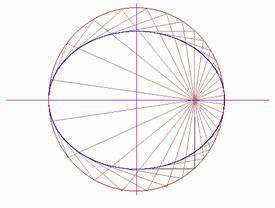Elipsa jest antypoderą okręgu, jeżeli spodek podery należy do wnętrza koła. Spodek antypodery jest ogniskiem elipsy.

Rysujemy koło i obieramy dowolny punkt, nie leżący na okręgu, ani nie będącym środkiem koła. Przykładamy ekierkę w ten sposób, że jej wierzchołek dotyka okręgu, a jedno z ramion przechodzi przez wybrany punkt. Ciągniemy następnie linię przez drugie ramię ekierki. Zmieniamy położenie wierzchołka ekierki, itd. Obwiednią (p. 4) narysowanych linii jest:

• elipsą, jeżeli wybrany punkt należy do wnętrza koła,
• hiperbolą, jeżeli wybrany punkt jest punktem zewnętrznym.

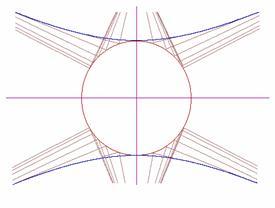Hiperbola jest antypoderą okręgu, jeżeli spodek podery znajduje się na zewnątrz koła. Spodki podery są ogniskami hiperboli.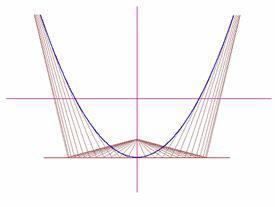

Parabola jest antypoderą prostej, jeżeli spodek podery nie należy do tej prostej. Punkt ten jest ogniskiem paraboli.