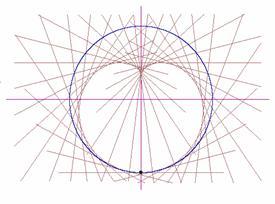
Kiedy promień świetlny odbija się od krzywej, obwiednia (p. 4) odbitych promieni nosi nazwę kaustyki lub katakaustyki [5].
KAUSTYKA WZGLĘDEM WYBRANEGO PUNKTU
...
160 x0 = y0
170 kp = (ye–y0)/(xe-x0)
180 ko = (2*k+kp*k^2*kp)/(2*kp*k-k^2+1)
...
Oznaczamy:
kp- współczynnik kierunkowy promienia padającego,
ko - współczynnik kierunkowy promienia odbitego.
Korzystamy z prawa odbicia światła, oraz dwukrotnie z wzoru na tangens kąta między prostymi o znanych współczynnikach kierunkowych:
tgφ = k1-k2 1+k1k2 Stosując dwukrotnie ten wzór otrzymujemy:
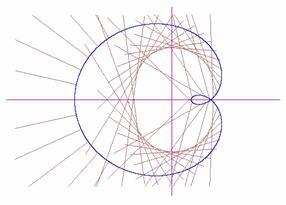
kp-k = ko-k , stąd ko = 2k+kpk2-kp 1+kpk 1+kok 2kpk-k2+1 Obwiednie promieni odbitych tworzą szukane kaustyki (p. Rys. 7.1, 7.2).
Rys. 7.1 Względem punktu (0,r), r – promień okręgu.
Rys. 7.2 Względem punktu (x,0), x < 0
Jeżeli pragniemy uwidocznić na rysunku promienie padające, kładziemy: LINE (0,y)- (x,y), kolor w dowolnym miejscu pętli 100.
KAUSTYKA W WIĄZCE RÓWNOLEGŁEJ
Zmodyfikujmy nasz program dla wiązki równoległej. (kp → ∞). Współczynnik kierunkowy wszystkich promieni odbitych ko liczymy jako odpowiednią granicę:
| ko = | lim | 2k+kpk2-kp | = | k2-1 |
| k0→ ∞ | 2kpk-k2+1 | 2k |
Wyłączamy linie 160 i 170.
... | Dla wiązki równoległej do osi OY (Rys. 7.3). Jeżeli pragniemy uwidocznić na rysunku promienie padające, kładziemy: LINE (x,0) (x,y), kolor w dowolnym miejscu pętli 100. |
... | Dla wiązki równoległej do osi OX (Rys. 7.4). Jeżeli pragniemy uwidocznić na rysunku promienie padające, kładziemy: LINE (0,y) (x,y), kolor w dowolnym miejscu pętli 100. |
Rys. 7.3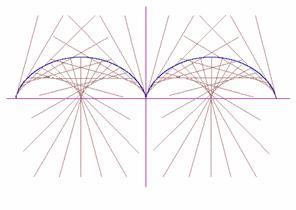 W promieniach równoległych do osi OY. | Rys. 7.4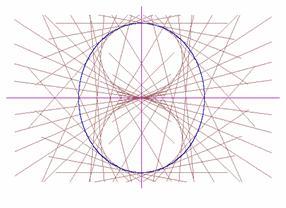 W promieniach równoległych do osi OX. |
GNU Free Documentation License.
Źródło: mgr Tadeusz Sypek