JustPaste.it

Miejsca zerowe funkcji - Równania liniowe

5a9ae7421973946635673a6dd5d8254a.gif

Funkcja liniowa posiada następujący przepis:

f(x) = ax + b

Nazwa funkcji liniowej pochodzi stąd, iż jej wykres jest linią prostą.

Miejsce zerowe xo funkcji liniowej obliczamy analitycznie:

f(xo) = axo + b
f(xo) = 0

axo + b = 0  /  + (-b)
axo = - b  /  : a
xo = -   b   ,  a 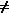fd97be1b047e25103cd24a4e3148a8a9.gif 0
a

Jeśli współczynnik a jest równy 0, to na wartość funkcji nie mają wpływu jej argumenty - mówimy wtedy, iż jest to funkcja stała. Jej wykresem będzie linia prosta równoległa do osi OX. Odległość tej prostej od osi OX jest równa współczynnikowi b. Jeśli współczynnik b jest również równy 0, to funkcja przyjmuje wartość 0 dla wszystkich swoich argumentów - rozwiązaniem jest cały zbiór liczb rzeczywistych, czyli brak jednoznacznego rozwiązania. Jeśli b jest różne od 0, to funkcja nie posiada miejsca zerowego. gdyż dla żadnego swojego argumentu nie przyjmuje wartości 0.

Jeśli współczynnik a jest różny od 0, miejsce zerowe wyznaczamy zgodnie z wyprowadzonym wzorem.

Ponieważ współczynnik a mógł być uzyskany na drodze wcześniejszych obliczeń numerycznych i może zawierać błędy zaokrągleń, to przy porównaniu z zerem musimy zastosować podane we wstępie zasady. Otóż zamiast zwykłego sprawdzania czy:

a = 0

zastosujemy test:

| a | < ε

gdzie ε jest wybraną dokładnością przyrównania do 0. Sądzę, iż ε = 0.0000000001 powinno być w większości typowych przypadków wystarczająco dokładne (jeśli nie, to należy je odpowiednio dostosować).

731c84fc950fa95ce6553f9ad5087aac.gif

Dane wejściowe

a,b - współczynniki a,b e3d7151a05d4ec071e285838aae2bcd3.gif R

Dane wyjściowe

xo - miejsce zerowe:  xo e3d7151a05d4ec071e285838aae2bcd3.gif R  lub informacja, iż rozwiązanie nie istnieje

Zmienne pomocnicze

ε - dokładność porównania z zerem. ε e3d7151a05d4ec071e285838aae2bcd3.gif R,  ε = 0.0000000001
40b30ec3d4c6857e3e7c11d5c89f6e22.gif
krok 1: Czytaj współczynniki a i b
krok 2: Jeśli | a | < ε , to idź do kroku 6
krok 3:
xo 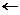8af230652b57094af69113023bfc1b8f.gif -   b 
a
krok 4: Pisz xo
krok 5: Zakończ algorytm
krok 6: Pisz "Brak miejsca zerowego"
krok 7: Zakończ algorytm
5744ee187bb73302636ba6a3643be23d.gif

 

Wykonanie algorytmu rozpoczynamy od odczytania współczynników a i b wchodzących w skład przepisu funkcji liniowej:

f(x) = ax + b

Następnie sprawdzamy, czy współczynnik a jest równy (dostatecznie bliski) zeru.

Jeśli nie, to wyznaczamy miejsce zerowe xo i wypisujemy je kończąc algorytm.

Jeśli tak, to funkcja f(x) nie posiada jednoznacznego miejsca zerowego (dla b różnego od 0 miejsce takie nie istnieje). Wypisujemy odpowiedni tekst i kończymy algorytm.


9fdeaf612f06d060149a067f639582ea.gif
5b594dba3e472a338d4aff936a8936bb.gif    
   
   

93c21c1b9670aadbfdae81b16fde2c6c.gif

Poniższe, przykładowe programy są praktyczną realizacją omawianego w tym rozdziale algorytmu. Zapewne można je napisać bardziej efektywnie. To już twoje zadanie. Dokładny opis stosowanych środowisk programowania znajdziesz we wstępie. Programy przed opublikowaniem w serwisie edukacyjnym zostały dokładnie przetestowane. Jeśli jednak znajdziesz jakąś usterkę (co zawsze może się zdarzyć), to prześlij o niej informację do autora. Pozwoli to ulepszyć nasze artykuły. Będziemy Ci za to wdzięczni.

  
       

W celu uruchomienia przykładów zastosuj projekt aplikacji konsoli (ang. Console Application).

Wydruk z uruchomionego programu 
Znajdowanie miejsca zerowego dla f(x) = ax + b
----------------------------------------------
(C)2006 mgr Jerzy Wałaszek     I LO w Tarnowie

Podaj współczynniki a i b

a = 12

b = -3

----------------------------------------------
WYNIK

x0 = 0,2500

----------------------------------------------
Koniec. Naciśnij klawisz Enter...
Microsoft Visual Basic 2005 Express Edition

 

Borland
Delphi 7.0
Personal
Edition		 
// Program oblicza miejsce zerowe dla funkcji liniowej
// f(x) = ax + b
//----------------------------------------------------
// (C)2006 mgr Jerzy Wałaszek
// I Liceum Ogólnokształcące
// im. Kazimierza Brodzińskiego
// w Tarnowie
//----------------------------------------------------

program mzfl1;

{$APPTYPE CONSOLE}

const
  EPS = 0.0000000001; // dokładność porównania z zerem
var
  a,b,x0 : real;
begin
  writeln('Znajdowanie miejsca zerowego dla f(x) = ax + b');
  writeln('----------------------------------------------');
  writeln('(C)2006 mgr Jerzy Walaszek     I LO w Tarnowie');
  writeln;
  writeln('Podaj wspolczynniki a i b');
  writeln;
  write('a = '); readln(a);
  writeln;
  write('b = '); readln(b);
  writeln;
  writeln('----------------------------------------------');
  writeln('WYNIK');
  writeln;
  if abs(a) < EPS then
    writeln('Brak miejsca zerowego')
  else
  begin
    x0 := - b / a;
    writeln('x0 = ',x0:10:4);
  end;
  writeln;
  writeln('----------------------------------------------');
  writeln('Koniec. Nacisnij klawisz Enter...');
  readln;
end.
Borland
C++ Builder
6.0
Personal
Edition		 
// Program oblicza miejsce zerowe dla funkcji liniowej
// f(x) = ax + b
//----------------------------------------------------
// (C)2006 mgr Jerzy Wałaszek
// I Liceum Ogólnokształcące
// im. Kazimierza Brodzińskiego
// w Tarnowie
//----------------------------------------------------

#include <iostream>
#include <iomanip>
#include <math>

using namespace std;

int main(int argc, char* argv[])
{
  const double EPS = 0.0000000001;
  double a,b,x0;

  cout.precision(4);     // 4 cyfr po przecinku
  cout.setf(ios::fixed); // format stałoprzecinkowy

  cout << "Znajdowanie miejsca zerowego dla f(x) = ax + b\n"
          "----------------------------------------------\n"
          "(C)2006 mgr Jerzy Walaszek     I LO w Tarnowie\n\n"
          "Podaj wspolczynniki a i b\n\n"
          "a = ";
  cin >> a;
  cout << "\n\nb = ";
  cin >> b;
  cout << "\n\n----------------------------------------------\n"
          "WYNIK\n\n";
  if(fabs(a) < EPS)
    cout << "Brak miejsca zerowego\n";
  else
  {
    x0 = - b / a;
    cout << "x0 = " << x0 << endl;
  }
  cout << "\n----------------------------------------------\n";
  system("pause");
  return 0;
}
Microsoft
Visual
Basic 2005
Express
Edition		 
' Program oblicza miejsce zerowe dla funkcji liniowej
' f(x) = ax + b
'----------------------------------------------------
' (C)2006 mgr Jerzy Wałaszek
' I Liceum Ogólnokształcące
' im. Kazimierza Brodzińskiego
' w Tarnowie
'----------------------------------------------------

Module Module1

  Sub Main()
    Const EPS As Double = 0.0000000001
    Dim a, b, x0 As Double

    Console.WriteLine("Znajdowanie miejsca zerowego dla f(x) = ax + b")
    Console.WriteLine("----------------------------------------------")
    Console.WriteLine("(C)2006 mgr Jerzy Wałaszek     I LO w Tarnowie")
    Console.WriteLine()
    Console.WriteLine("Podaj współczynniki a i b")
    Console.WriteLine()
    Console.Write("a = ") : a = Val(Console.ReadLine)
    Console.WriteLine()
    Console.Write("b = ") : b = Val(Console.ReadLine)
    Console.WriteLine()
    Console.WriteLine("----------------------------------------------")
    Console.WriteLine("WYNIK")
    Console.WriteLine()
    If Math.Abs(a) < EPS Then
        Console.WriteLine("Brak miejsca zerowego")
     Else
      x0 = -b / a
      Console.WriteLine("x0 = " + Format(x0, "####0.0000"))
    End If
    Console.WriteLine()
    Console.WriteLine("----------------------------------------------")
    Console.WriteLine("Koniec. Naciśnij klawisz Enter...")
    Console.ReadLine()
  End Sub

End Module
Python 
# -*- coding: cp1250 -*-
# Program oblicza miejsce zerowe dla funkcji liniowej
# f(x) = ax + b
#----------------------------------------------------
# (C)2006 mgr Jerzy Wałaszek
# I Liceum Ogólnokształcące
# im. Kazimierza Brodzińskiego
# w Tarnowie
#----------------------------------------------------

EPS = 0.0000000001 # dokładność porównania z zerem

print "Znajdowanie miejsca zerowego dla f(x) = ax + b"
print "----------------------------------------------"
print "(C)2006 mgr Jerzy Walaszek     I LO w Tarnowie"
print
print "Podaj wspolczynniki a i b"
print
a = float(raw_input("a = "))
print
b = float(raw_input("b = "))
print
print "----------------------------------------------"
print "WYNIK"
print
if abs(a) < EPS:
  print "Brak miejsca zerowego"
else:
  x0 = -b / a
  print "x0 = %10.4f" % x0
print
print "----------------------------------------------"
raw_input("Koniec. Nacisnij klawisz Enter...")
JavaScript 
<html>
  <head>
  </head>
  <body>
    <div align="center">
      <form style="BORDER-RIGHT: #ff9933 1px outset;
                   PADDING-RIGHT: 4px;
                   BORDER-TOP: #ff9933 1px outset;
                   PADDING-LEFT: 4px;
                   PADDING-BOTTOM: 1px;
                   BORDER-LEFT: #ff9933 1px outset;
                   PADDING-TOP: 1px;
                   BORDER-BOTTOM: #ff9933 1px outset;
                   BACKGROUND-COLOR: #ffcc66" name="frmprg">
        <h3 id="out_t" style="TEXT-ALIGN: center">
          Znajdowanie miejsca zerowego dla <i>f(x) = ax + b</i>
        </h3>
        <p style="TEXT-ALIGN: center">
          (C)2006 mgr Jerzy Wałaszek&nbsp;&nbsp;&nbsp;&nbsp; I LO w Tarnowie
        </p>
        <hr>
        <p style="TEXT-ALIGN: center">
          Podaj wartości współczynników <i>a</i> i <i>b</i>:
        </p>
        <p style="TEXT-ALIGN: center">
          <i>a</i> =
<input type="text" name="inp_a" size="20" value="25" style="text-align: right">
          &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
          <i>b</i> =
<input type="text" name="inp_b" size="20" value="-5" style="text-align: right">
        </p>
        <p style="TEXT-ALIGN: center">
<input type="button" value="Oblicz miejsce zerowe" name="B1" onclick="main()">
        </p>
        <hr>
        <p style="TEXT-ALIGN: center">
          <b>WYNIK:</b>
        </p>
        <p style="TEXT-ALIGN: center" id="t_out">.</p>
      </form>

<script language=javascript>

// Program oblicza miejsce zerowe dla funkcji liniowej
// f(x) = ax + b
//----------------------------------------------------
// (C)2006 mgr Jerzy Wałaszek
// I Liceum Ogólnokształcące
// im. Kazimierza Brodzińskiego
// w Tarnowie
//----------------------------------------------------

function main()
{
  var EPS = 0.0000000001;
  var a,b,x0,t;

  a = parseFloat(document.frmprg.inp_a.value);
  b = parseFloat(document.frmprg.inp_b.value);

  if(isNaN(a) || isNaN(b))
    t = "<b><font color=red>Złe współczynniki</font></b>";
  else
  {
    if(Math.abs(a) < EPS)
      t = "<b><font color=red>Brak miejsca zerowego</font></b>";
    else
    {
      x0 = - b / a;
      t = "x<sub>o</sub> = " + x0;
    }
  }
  document.getElementById("t_out").innerHTML = t;
}

</script>
    </div>
  </body></html>
 
Dokument ten rozpowszechniany jest zgodnie z zasadami licencji
GNU Free Documentation License.
   document.frmadminemail.adminemail_tytul.value = parent.document.title + " : " + document.title;  

 

Źródło: mgr Jerzy Wałaszek

technologia programowanie