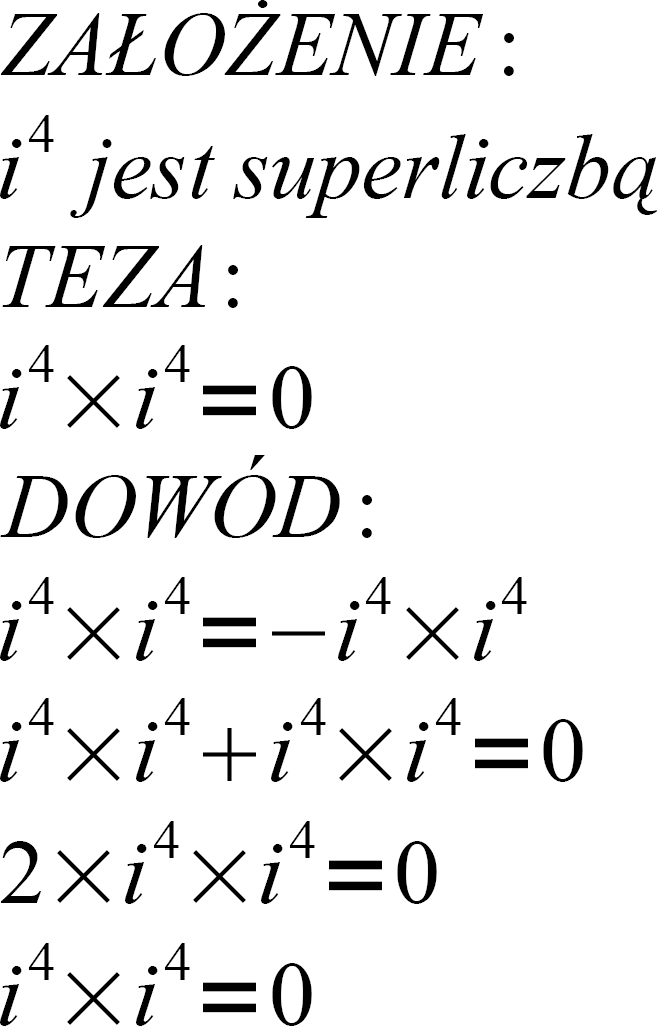Superliczby to liczby Grassmanna. Może więcej o genialnym niemieckim matematyku następnym razem? Dzisiaj uważniej przyjrzymy się postaci innego wybitnego matematyka...

Na początku kilka sprostowań...
Być może wielu z Was słyszało coś o „Boskiej cząstce”, czyli cząstce Higgsa, zwanej również bozonem Higgsa. Tym problemem, tzn. czy cząstka ta istnieje, czy nie, Teoria Superstrun akurat nie zajmuje się. Bozon Higgsa, według teorii modelu standardowego, ma być odpowiedzialny za masę innych cząstek. Prawdą jest, że jej jeszcze nie wykryto i raczej nie prędko to nastąpi (może wcale!) i kto wie, czy właśnie z tego powodu model standardowy nie ulegnie znacznej modyfikacji. Nota bene ma on (model standardowy) obecnie olbrzymie kłopoty eksperymentalne, gdyż są znaczne różnice między teorią modelu standardowego, a doświadczeniami. Może o tym więcej napiszę w innym cyklu, kiedyś przy okazji innych problemów naukowych. Przejdźmy jednak do Teorii Superstrun i jej problemów. W Teorii Superstrun cząstki elementarne są modelowane jako drgające w wielu wymiarach pętle, tylko nie wiadomo z czego te pętle miałyby być „zrobione”? Ktoś kiedyś powiedział, że „Teoria Superstrun to odprysk fizyki XXI wieku, który przypadkowo wpadł do fizyki XX wieku”. Nie jest jednak tak słodko - Teoria ta napotyka również na ogromne kłopoty, nie tylko z powodu kosmicznego aparatu matematycznego, ale również z pewnych przyczyn zasadniczych. Istnieje przypuszczenie, że teoria ta może być jednak ślepym zaułkiem fizyki. Nie wszystko co matematycznie eleganckie, musi być fizycznie słuszne. Ale nie wykluczone, że za 50 lat dzieciaki w przedszkolach będą się uczyć o Teorii Superstrun w zarysie i będą o niej śpiewać piosenki. Jeszcze „małe ale” o Superliczbach:
Superliczby to liczby Grassmanna, gdy zmieniają kolejność, to ta zmiana pociąga za sobą zmianę znaku. Czyli:
a x b = - b x a.
Zasada przemienności mnożenia nie obowiązuje. To już nie są liczby rzeczywiste, a więc nasze przyzwyczajenia, że a x b = b x a nie sprawdza się dla superliczb. Dziwne co? :) Może więcej o genialnym niemieckim matematyku następnym razem?
Dzisiaj uważniej przyjrzymy się postaci innego wybitnego matematyka, matematyka najwyższej klasy, który przyczynił się najbardziej do powstania Teorii Superstrun:
- czyli mowa o Hindusie Srinivasie Ramanujanie.
Srinivasa Ramanujan urodził się w 1887 r. w Erode, w mieście na południu Indii - niedaleko Madrasu. Pochodził z biednej rodziny, z kasty braminów. Ojciec Ramanujana pracował jako urzędnik w sklepie odzieżowym. Nauczyciele Ramanujana przewidzieli, gdy był jeszcze dzieckiem, że ma wybitne zdolności. Kiedy tylko nauczył się podstaw trygonometrii, odkrył szereg praw rządzących sinusami i cosinusami. Był bardzo zaskoczony, kiedy dowiedział się później, że te prawa są już odkryte przez pewnego genialnego szwajcarskiego matematyka, Leonarda Eulera, ponad sto lat wcześniej. Już około 10 roku życia zasłynął w wiosce z powodu niespotykanych umiejętności rachunkowych, między innymi samodzielnie ustalił tożsamość Eulera. Jak pewnie prawie każdy człowiek, miał Ramanujan przyjaciela, który starał się mu pomóc. Przyjaciel ów pożyczył z biblioteki książkę o matematyce, specjalnie dla Ramanujana. Książka ta była zatytułowana: „Synopsis of Elementary Results in Pure Mathematics”. Jej Autorem był Georga S. Carra z Uniwersytetu w Cambridge. Ramanujan miał wtedy 16 lat.
Był to pierwszy kontakt z zachodnią matematyką poprzez lekturę książki Georga S. Carra, z której zaczął udowadniać twierdzenia. Praca Carra była po prostu wyliczeniem około 5000 twierdzeń z dziedziny algebry, trygonometrii, rachunku różniczkowego i geometrii analitycznej. Jednak dla młodego miłośnika liczb książka ta stała się przyczyną czegoś w rodzaju objawienia. Nagle okazało się, że Ramanujan zna i kocha liczby. Ta właśnie książka spowodowała obudzenie się w nim geniuszu. Wedle powszechnej opinii, nikt nie był w stanie prześcignąć Ramanujana w matematyce. Kiedy np. nauczyciel w rządowym college’u w Kumbakonam zapisywał dwie tablice w celu rozwiązania jakiegoś problemu trygonometrycznego lub algebraicznego, przy czym czynił to w 10 lub 11 etapach (trudnych do zrozumienia dla większości uczniów), Ramanujan prosił o pozwolenie skrócenia rozwiązania i rozwiązywał problem w 2 lub 3 krokach - tłumacząc przy tym każdy pojedynczy krok nauczycielowi. Zajmował się często matematyką na innych wykładach. W szkole średniej słabo sobie radził, nudziły go zadania domowe i ciągle przeprowadzał własne obliczenia. Uciekł z domu, a potem znów wrócił, ale niestety zachorował i znów się nie dostał do szkoły. W rezultacie został pozbawiony stypendium i wyrzucony z college’u. Po kilku nieudanych próbach wznowienia nauki powrócił do domu. Później jeszcze próbował zdać egzamin końcowy, jednak bez powodzenia.
W wieku 25 lat, z pomocą przyjaciół zdobył posadę niższego urzędnika w Port Trust w Madrasie, z niskim wynagrodzeniem, w wysokości 20 funtów na rok, z czego utrzymywał swoją młodą żonę oraz matkę, mieszkającą razem z nimi. Jednakże prawdziwym zajęciem Ramanujana była zawsze matematyka. W pracy miał czas na dalsze rozwijanie swoich zainteresowań matematyką. Lubił również liczyć coś na kartkach, leżąc na brzuchu na pryczy na werandzie, którą dzielił z licznymi współlokatorami swego domu. Zaczynał pisać, kiedy zmniejszał się codzienny upał. Jego żona - Janaki oraz matka podawały mu obiad, podczas gdy on zapisywał swoje kartki, strona po stronie. Nieraz pisał do 6 rano, po czym zasypiał na krótko, aby stawić się do swojej urzędniczej pracy. Być może stan ten pozostałby niezmieniony przez większość czasu jego życia, że był matematykiem w nocy i urzędnikiem w ciągu dnia, gdyby nie dyrektor zarządu, który rozpoznał jego matematyczny geniusz. Nakłonił Ramanujana, aby wysłał niektóre ze swych prac do matematyków brytyjskich i postarał się o ich poparcie. Spragniony kontaktu z innymi matematykami wysłał listy ze 120 twierdzeniami do trzech znanych brytyjskich matematyków, z których dwóch zignorowało tą korespondencję. Jeden z listów Ramanujana, datowany na 16 stycznia 1913 r., a adresowany do matematyka G. H. Hardy’ego z Cambridge, został pobieżnie przeczytany i zignorowany. Hardy, choć początkowo odrzucił wyniki Ramanujana, po przedyskutowaniu ich z innymi matematykami zmienił jednak zdanie. Z początku uznał list Ramanujana za plagiat, jednak 16 stycznia 1913 r., po spotkaniu z Johnem Littlewoodem, ponownie mu się przyjrzał i obok znanych twierdzeń znalazł także dotąd nieznane. „Nigdy niczego podobnego nie widziałem” - pisał później Hardy - „Muszą być prawdziwe, bo... po prostu nikt nie miałby tyle wyobraźni, aby je wymyślić”. Wkrótce potem Ramanujan przyjął zaproszenie Hardy’ego i przybył do Anglii w 1914 r.. W Cambridge został bardzo ciepło przyjęty i nieomal natychmiast zaczął tworzyć olśniewające prace. Jednakże kilka miesięcy później Anglia przystąpiła do I wojny światowej. Chociaż ściął włosy i zamienił swój turban na kapelusz (którego nie znosił) i unikał, kiedy tylko mógł noszenia butów i skarpetek. Wilgotny chłodny klimat był dla niego męczarnią i w maju 1917 r. Hardy zawiadomił uniwersytet w Madrasie, że Ramanujan cierpi najprawdopodobniej na nieuleczalną chorobę. Niektórzy sądzili później, że mógł zachorować na gruźlicę, jednak objawy nie były typowe. Być może chorobę spowodował znaczny niedobór witamin. Nie ma w każdym razie jednolitego poglądu na przyczynę choroby. Przez trzy lata Ramanujan współpracował z Hardym w Trinity College. Często bywał w sanatoriach. Do Indii powrócił po I wojnie światowej w 1919 r. w bardzo złym stanie fizycznym, gdzie zmarł rok później, w wieku zaledwie 32 lat. Ramanujan jeszcze przez rok czasu przed śmiercią tworzył twierdzenie za twierdzeniem, choć był bardzo osłabiony nieznaną chorobą. Tuż przed śmiercią był nieprzytomny przez prawie 4 dni.
Niektóre z najbardziej znanych prac Ramanujana dotyczą czegoś, co pozornie wydaje się dziecinną zabawą, a co matematycy nazywają problemem podziału. Zagadnienie to polega na wykazaniu, na ile sposobów liczba całkowita może być przedstawiona jako suma innych liczb całkowitych. Np. liczbę 4 można przedstawić na 5 różnych sposobów:
3+1; 2+2; 2+1+1; 1+1+1+1; oraz sama 4.
Kiedy liczba staje się większa, tego rodzaju jej przedstawienie przestaje być dziecinną zabawą. Np. ilość podziałów liczby 200 wynosi 4 biliony! Jednym z największych osiągnięć Ramanujana i Hardy’ego był sposób na obliczenie ilości podziałów dowolnej liczby. Jest to długi, skomplikowany wzór, wymagający ciągłych iteracji i wykorzystujący ponadto dwa krótsze wzory. Krotność powtarzania tych obliczeń zależy również od pierwiastka kwadratowego dzielonej liczby! Wyniki Ramanujana dotyczące zagadnienia podziału okazały się niezwykle użyteczne dla fizyków teoretycznych pracujących nad superstrunami. Zgodnie z tą teorią obiekty wszechświata istnieją dzięki drganiom nieskończenie małych strun zwiniętych w ciasne pętle, przy czym długość takiej struny wynosi zaledwie 10 -33 cm. Ruch strun powoduje powstawanie cząsteczek według reguły im bardziej intensywny ruch, tym cięższa cząsteczka. Cząsteczki dzielą się na lżejsze, które mogą być postrzegane, i cięższe istniejące jedynie teoretycznie. Ruch strun ma odbywać się, zgodnie z teorią, w dziewięciu wymiarach przestrzennych i jednym czasowym, jednakże naszymi ograniczonymi ludzkimi zmysłami, dysponując niedostatecznie mocnymi akceleratorami cząsteczkowymi, nie możemy postrzegać sześciu z nich. Co więcej, chociaż ruchy strun odbywają się w świecie dziesięciowymiarowym, wewnątrz każdej z nich istnieje jeszcze 16 dalszych wymiarów. Jednakże dzięki matematyce można badać ten fantastyczny świat, przy czym najbardziej pomocne są tu prace Ramanujana. Zdaniem Jeffreya Herveya, jednego z fizyków z tzw. kwartetu smyczkowego, którego członkowie są autorami Teorii Superstrun, teoria podziałów jest ich podstawowym narzędziem pracy. Matematyka Ramanujana znajduje jednak również inne zastosowania. „W fizyce jest tyle problemów kombinatorycznych, różnego typu obliczeń, ile istnieje obiektów danego rodzaju” - mówi Carlo Moreno z uniwersytetu w Nowym Yorku. Kiedy fizycy starali się zgłębić tajemnice budowy atomu, kluczem do jej poznania stała się teoria podziału. Dzięki matematyce można było zainteresować się, na ile sposobów elektrony mogą być rozmieszczone wokół jądra atomowego.
Ramanujan nie byłby zdziwiony zainteresowaniem matematyków jego równaniami. Twierdził wszak sam, że jego matematyka stanie się użyteczna dopiero za 100 lat - tak mówi w każdym razie jego żona, Janaki, która niedawno udzieliła wywiadu. Jednakże niewątpliwie - leżąc na swej pryczy i ledwie zauważając podaną mu przez żonę garstkę ryżu - nie mógł przewidzieć, że tworzy niektóre podstawy nauki dziewięćdziesiątych lat XX wieku. Jego prace legły u podstaw Teorii Superstrun, teoretycznych obiektów, które - zdaniem niektórych fizyków - tworzą wielowymiarowy szkielet wszelkiej materii. Przyczyniły się one również do rozwoju programów komputerowych. Ramanujan przekazywał swą wiedzę bez przestrzegania jakichkolwiek przyjętych zasad. Żyjący w biedzie i niedokształcony, nie zwracał zbyt wielkiej uwagi na czynienie wyjaśnień. Pomijał ogromne partie swego rozumowania, tak, że śledzący jego prace nieustannie zadają sobie pytanie: „Skąd to się wzieło?”
C. D. N.
W RAMACH WSTĘPU DO CZ. III - PRZEDSTAWIAM KOLEJNY DOWÓD, WŁASNOŚCI JAKĄ MAJĄ SUPERLICZBY!!! OTÓŻ ICH ILOCZYN JEST RÓWNY ZERO!!!