Prognozowanie rozgrywki grą planszową

Dawno temu czyjeś zajęcie zainspirowało mnie do skonstruowania ciekawego algorytmu i programu komputerowego. Napisałem opowiadanie-artykuł. Teraz dedykuję je Ani, która odeszła.

- Cześć Anka! Co ty tam gryzmolisz?

- Witaj dowcipasku. A ja po prostu projektuję grę planszową dla uczniów podstawówki. Nawet nie masz pojęcia Marku, jak są ciekawe przygód, które im, co tydzień w ten sposób zapewniam.

- Rozumiem, że pomagasz mamie nauczycielce, ale dlaczego poświęcasz temu tyle pracy, a efekt plastyczny jest jednak znacznie słabszy niż gier z drukarni, których tyle jest na rynku?

- Mama ma swój autorski program nauczania i chce żeby dzieci poznawały określone słowa, zwroty, sytuacje i żeby to było wplecione w zabawę. Nie ma takich gier na rynku.

- A czy te dzieci dają radę nauczyć się co tydzień nowej gry?

- Dostają szczegółową instrukcję, a gra jest typową grą z kostką i jednym pionkiem dla każdego gracza. Ale mam z nią inny problem. Okazuje się bowiem, że czas rozgrywki jest dla niektórych moich plansz zbyt długi przekraczając te czterdzieści minut, a dla innych zbyt krótki i dzieci są zawiedzione. Może ty jako matematyk mógłbyś mi pomóc tak projektować grę by trwała pomiędzy pół godziny a czterdzieści minut?

- Na to nie ma gotowego wzoru, a poza tym wiele zależy od tego jak szybko sobie podają kostkę, rzucają i dodatkowo dyskutują. Ale jak widzę u ciebie pola są ponumerowane od 0 do pewnej liczby n, więc pewnie dużo zależy jaka to liczba. Można tu podać następujący wzór na średnią liczbę rzutów jakie musi wykonać jeden gracz by przejść od początku do końca: n/3,5.

- To jest oczywiste, że im więcej pól tym gra dłużej trwa, ale miałam już kilka przypadków gier o równej liczbie pól i zupełnie różnych czasach rozgrywek dla nich.

- Ach widzę, że jeszcze masz wiele pól z nagrodami i karami.

- Zatrzymanie się na takim polu po rzucie kostką powoduje, że gracz jest zmuszany do przejścia na zupełnie inne pole planszy przez odliczenie pól kary lub nagrody.

- To komplikuje obliczenia, ale mogę spróbować je zrobić dla tej twojej planszy.

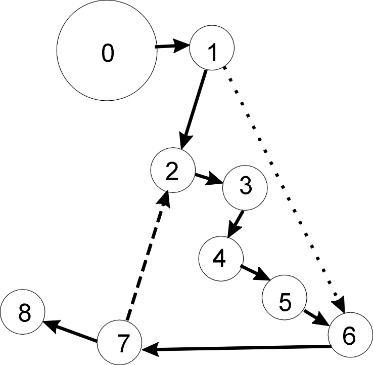
Wychodząc z pola zero prawdopodobieństwo zatrzymania się w jednym rzucie na polach od 1 do 6 wynosi po 1/6. Zróbmy więc tabelkę:

Teraz możemy doliczyć prawdopodobieństwo z pola 1 do pola 6, bo tam zostanie automatycznie przeniesiony pionek jak zatrzyma się na polu 1..

W kolejnym rzucie prawdopodobieństwa znowu się podzielą przez 6, a że rzuty będą następowały z pól 2,3,4,5,6 to będzie to tak wyglądało. Nie będzie rzutu z 1, bo tu pionek przeniesie się na 6 i z 6 będzie do podzielenia większe prawdopodobieństwo:

- A z 7 pradobodobieństwo przeniesie się na 2.

- I teraz znowu to prawdopodobieństwo powróciło na początkowe pola i trzeba będzie liczyć od nowa. Daj mi trochę czasu to ci to wszystko ze spokojem powyliczam.

- Ale ładna tabelka. Tylko gdzie ja tu znajdę ile potrwa ta gra?

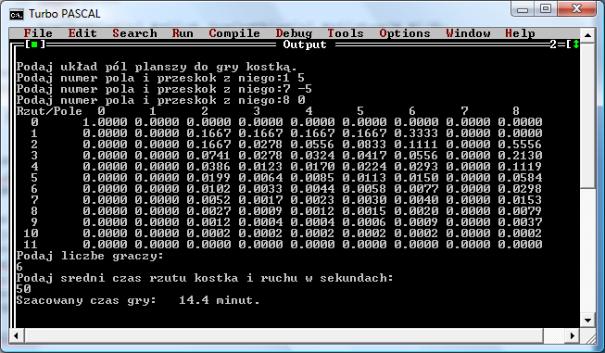
- Teraz wystarczy, że elementy ostatniej kolumny czyli prawdopodobieństwa dotarcia do ostatniego pola przemnożymy przez liczbę rzutów, liczbę osób uczestniczących w grze i czas na wykonanie pojedynczego rzutu, a wyjdzie nam średni czas trwania gry. Tutaj wyjdzie 14.4 minuty po przyjęciu, że uczestniczy sześciu graczy rzucających co pięćdziesiąt sekund.

- To trochę mało.

- No to wystarczy, że zwiększysz liczę pól i dodasz trochę więcej kar. Ale ja już mam dosyć tego liczenia na piechotę, wolę ci napisać program, który to będzie sam robił.

program GRA;

const

n=50;

m=80;

eps=0.001;

var

Los: array[0..n]of array[0..m]of extended;

Uklad: array[0..n]of integer;

z:boolean;

nn,p,r:integer;

function Rzut(P,R:integer):boolean;

var i,j:integer;

begin

   if Los[P,R]>eps

   then begin

      for i:=P+1 to P+6 do begin

         if i>nn

         then j:=nn

         else j:=i;

         Los[j,R+1]:=Los[j,R+1]+Los[P,R]/6;

         if Uklad[j]<>0

         then begin

            Los[j+Uklad[j],R+1]:= Los[j+Uklad[j],R+1]+Los[P,R]/6;

            Los[j,R+1]:=0;

         end;

      end;

      Rzut:=true;

   end

   else Rzut:=false;

end;

procedure Drukuj;

var i,j,g,k:integer;

s:extended;

begin

   write('Rzut/Pole');

   for j:=0 to nn do

      write(j:3,' ':4);

   writeln;

   for i:=0 to r do begin

      write(i:3,' ':6);

      for j:=0 to nn do

         write(Los[j,i]:0:4,' ');

      writeln;

   end;

   s:=0;

   for i:=0 to r do

     s:=s+Los[nn,i]*i;

   writeln('Podaj liczbe graczy:');

   readln(g);

   writeln('Podaj sredni czas rzutu kostka i ruchu w sekundach:');

   readln(k);

   writeln('Szacowany czas gry:',s*g*k/60:7:1,' minut.');

   readln;

end;

procedure Czytaj;

  var p,r,nast:integer;

begin

   for p:=0 to n do

      for r:=0 to m do

         Los[p,r]:=0;

writeln('Podaj ukˆad p¢l planszy do gry kostk¥.');

   nast:=-1;

   while(nast<>0)do begin

      write('Podaj numer pola i przeskok z niego:');

      readln(p,nast);

      Uklad[p]:=nast;

   end;

   nn:=p;

end;

begin

   Czytaj;

   r:=0;

   z:=true;

   Los[0,0]:=1;

   while z and (R<m) do begin

      z:= false;

      for p:=0 to nn-1 do

         z:= Rzut(p,r) or z;

      r:=r+1;

   end;

   Drukuj;

end.

- Spróbuję więc teraz skorzystać z twojego programu i wpiszę więcej pól:

45 -40

30 -20

20 20

50 0

I tyle co poprzednio graczy i czasu rzutu.

- No widzisz teraz wyszło znacznie więcej niż potrzebujesz, bo aż

80.6 minut. Musisz jeszcze poeksperymentować, a na pewno z łatwością będziesz uzyskiwała oczekiwane wyniki.