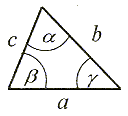
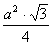Trójkąt jest wielokątem o trzech bokach | Suma miar kątów wewnętrznych trójkąta jest równa 180°. + +  + +  = 180°. = 180°. |
Każdy bok trójkąta jest mniejszy od sumy dwóch pozostałych boków tego trójkąta.
|AB| < |AC| + |BC|, |AC| < |AB| + |BC| i |BC| < |AB| + |AC|
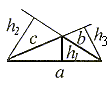
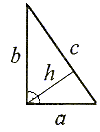
Wysokości trójkąta
Wysokością trójkąta nazywamu odcinek poprowadzony z wierzchołka trójkąta prostopadle do przeciwległego boku lub do przedłużenia tego boku.
Każdy trójkąt ma trzy wysokości, które przecinają sie w jednym punkcie zwanym ortocentrum (p.O).
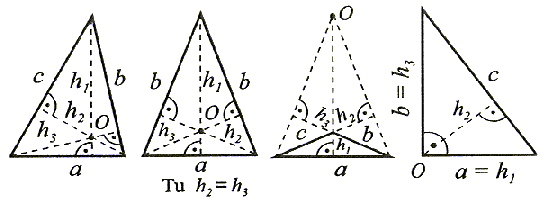
Środkowe boków trójkąta
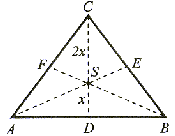 |DS| = 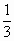 |CD|, |ES| = |CD|, |ES| = 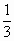 |AE| |AE|oraz |FS| = 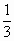 |BF| |BF| | Środkową boku trójkąta nazywamy odcinkiem łączącym środek tego boku z przeciwległym bokiem tego trójkąta. Każdy trójkąt ma trzy srodkowe przecinające się w jednym punkcie (p.S), który nazywamy środkiem ciężkości tego trójkąta. |
Punkt S (środek ciężkości) dzieli każdą środkową w stosunku 1:2, czyli:
|DS| =
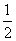 |CS|, |ES| =
|CS|, |ES| = 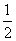 |AS| oraz |FS| =
|AS| oraz |FS| = 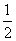 |BS|.
|BS|.Odcinki łączące środki boków trójkąta
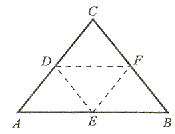 | Odcinki łączące środki boków trójkąta są równoległe do przeciwległych boków i równe ich połowie. |
DF||AB i |DF| =
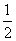 |AB|, EF||AC i |EF| =
|AB|, EF||AC i |EF| = 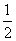 |AC| oraz DE||BC i |DE| =
|AC| oraz DE||BC i |DE| = 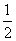 |BC|
|BC|Dwusieczne kątów trójkąta
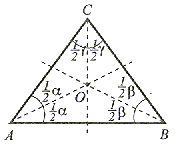 | Dwusieczna kąta jest to półprosta dzieląca kąt na połowy. Każdy trójkąt ma trzy dwusieczne przecinające się w jednym punkcie (p.O), który jest środkiem koła wpisanego w trójkąt. |
Symetralne boków trójkąta
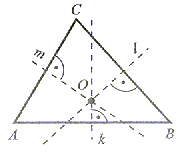 | Symetralną boku trójkąta nazywamy prostą prostopadłą do tego boku, przechodzącą przez jego środek. Każdy trójkąt ma trzy symetralne boków, przecinające się w jednym punkcie (p.O), który jest środkiem koła opisanego na tym trójkącie |
Środek O koła opisanego na trójkącie może leżeć wewnątrz lub na zewnątrz trójkąta, a w przypadku trójkąta prostokątngo na jego goku (w połowie przeciwprostokątnej).
Trójkąty nie mają środka symetrii.
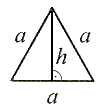
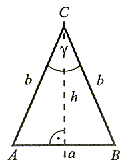 | Trójkąt równoramienny ma jedną oś symetrii i jest ona jednocześnie dwusieczną kąta ( ) zawartego między ramionami oraz pokrywa się z wysokością figury, symetralną i środkową podstawy. ) zawartego między ramionami oraz pokrywa się z wysokością figury, symetralną i środkową podstawy. |
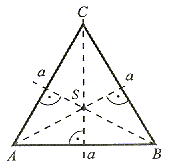 | Trójkąt równoboczny ma trzy osie symetrii, które są jednocześnie dwusiecznymi kątów, wysokościami, symetralnymi i środkowymi boków figury. |
Punkt przecięcia (C) osi symetrii jest środkiem koła wpisanego i opisanego na trójkącie równobocznym.
RODZAJE TRÓJKĄTÓW
| Podział trójkątów ze względu na boki | ||
| równoboczny (dowolny)  Każdy bok ma inną długość i każdy kąt ma inną miarę. | równoramienny Ma dwa boki równe i nazywamy je ramionami. Trzeci bok to podstawa. Kąty przy podstawie mają tę samą miarę. | równoboczny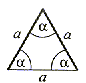 Ma wszystkie boki równej długości. Wszystkie kąty wewnętrzne są równe i mają po 60°. |
| Podział trójkątów ze względu na kąty | ||
| ostroktny (dowolny) 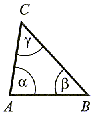  < 90° < 90° < 90° < 90° < 90° < 90°Każdy kąt wewnętrzny jest kątem ostrym. | prostokątny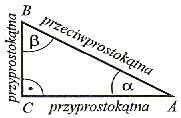 C = 90°,  < 90° i < 90° i  < 90° < 90°Ma jeden kąt prosty, a dwa pozostałe są ostre i takie, że  + +  = 90° = 90° | rozwarty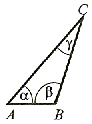  < 90° < 90° > 90° > 90° < 90° < 90°Ma jeden kąt rozwarty, a dwa pozostałe są ostre. |
PODZIAŁ TRÓJKĄTÓW ZE WZGLĘDU NA BOKI I KĄTY
ostrokątny | prostokątny | rozwartokątny | |
równoboczny (dowolny) | 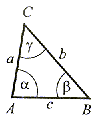  < 90° < 90° < 90° < 90° < 90° < 90° | 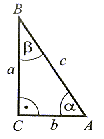  C = 90° C = 90° + +  = 90° = 90° | 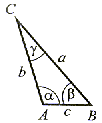 90° <  < 180° < 180° < 90° i < 90° i  < 90° < 90° |
równoramienny | 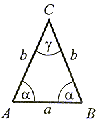  = =  , ,  < 90° < 90° < 90°, < 90°,  < 90° < 90° | 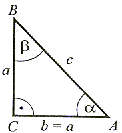  = =  = 45° = 45°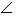 C = 90° C = 90° |   = =  , ,  < 90° < 90° < 90° < 90°90° <  < 180° < 180° |
równoboczny | 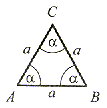  = 60° = 60° | Nie ma takiego trójkąta | Nie ma takiego trójkąta |
CECHY PRZYSTAWANIA TRÓJKĄTÓW
I cecha
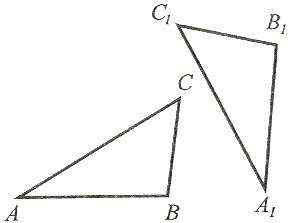 | Jeżeli boki jednego trójkąta są przystające (równe) do odpowiednich boków drugiego trójkąta, to te trójkąty są przystające. |
|AB| = |A1B1|, |BC| = |B1C1| oraz |AC| = |A1C1|, to
 ABC
ABC 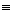
 A1B1C1
A1B1C1II cecha
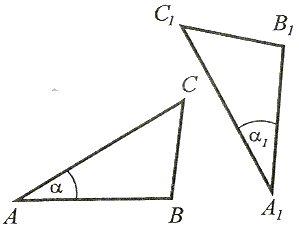 | Jeżeli dwa boki i kąt między nimi zawarty jednego trójkąta są przystające (równe) do odpowiednich boków i kąta zawartego między nimi w drugim trójkącie, to te trójkąty są przystające. |
|AB| = |A1B1|, |AC| = |A1C1| i
 =
=  1, to
1, to  ABC
ABC 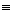
 A1B1C1
A1B1C1III cecha
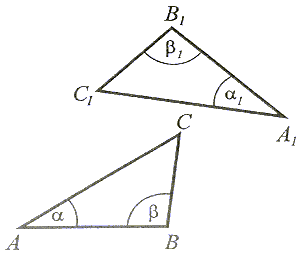 | Jeżeli bok i dwa kąty do niego przyległe jednego trójkąta są przystające (równe) do odpowiedniego boku i kątów do niego przyległych w drugim trójkącie, to te trójkąty są przystające. |
|AB| = |A1B1|,
 =
=  1 oraz
1 oraz  =
=  1, to
1, to  ABC
ABC 
 A1B1C1
A1B1C1CECHY PRZYSTAWANIA TRÓJKĄTÓW PROSTOKĄTNYCH
| I cecha | Przyprostokątne jednego trójkąta są odpowiednio równe (przystające) przyprostokątnym drugiego trójkąta. |
| II cecha | Przyprostokątna i kąt ostry do niej przeciwległy jednego trójkąta są odpowiednio równe przyprostokątnej i kątowi do niej przyległemu w drugim trójkącie. |
| III cecha | Przyprostokątna i kąt do niej przeciwległy jednego trójkąta są odpowiednio równe przyprostokątnej i kątowi do niej przyległemu w drugim trójkącie. |
| VI cecha | Przeciwprostokątna i jeden z kątów ostrych jednego trójkąta są odpowiednio równe przeciwprostokątnej i jednemu z kątów ostrych w drugim trójkącie. |
| V cecha | Przeciwprostokątna i jedna z przyprostokątnych jednego trójkąta są odpowiednio równe przeciwprostokątnej i jednej z przyprostokątnych w drugim trójkącie. |
CECHY PODOBIEŃSTWA TRÓJKĄTÓW
Własność, która pozwala na określenie podobieństwa pewnej rodziny figur, nazywa się cechą podobieństwa figur tej rodziny.
Wyróżniamy trzy cechy podobieństwa trójkątów:
I cecha
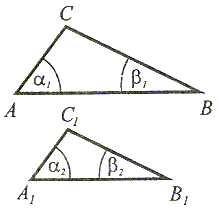  1 = 1 =  2 oraz 2 oraz  1 = 1 =  2 2 | Jeżeli dwa kąty jednego trójkąta są przystające do odpowiednich kątów drugiego trójkąta, to trójkąty te są podobne. |
II cecha
  | Jeżeli stosunki wszystkich boków jednego trójkąta do odpowiednich boków drugiego trójkąta są równe, to trójkąty są podobne. |
III cecha
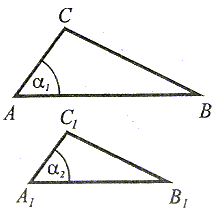 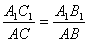 oraz  1 = 1 =  | Jeżeli stosunki dwóch boków jednego trójkąta do odpowiednich boków drugiego trójkąta są równe oraz kąty zawarte między tymi bokami są przystające (równe), to trójkąty te są podobne. |
CECHY PODOBIEŃSTWA TRÓJKĄTÓW PROSTOKĄTNYCH
I cecha
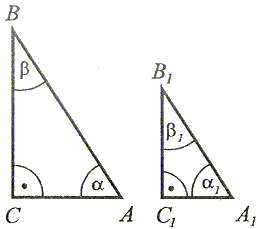  1 = 1 =  lub lub  1 = 1 =  | Jeżeli dwa trójkąty prostokątne mają po jednym kącie ostrym przystającym, to te trójkąty są przystające. |
II cecha
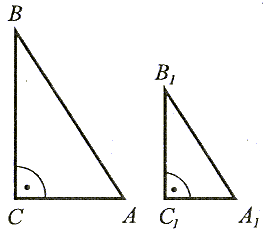 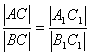 | Jeżeli stosunek długości przyprostokątnych jednego trójkąta jest równy stosunkowi długości przyprostokątnych drugiego trójkąta, to te trójkąty są podobne. |
III cecha
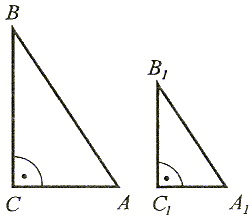 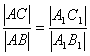 | Jeżeli stosunek długości przyprostokątnej do długości przeciwprostokątnej jednego trójkąta jest równy stosunkowi odpowiedniej przyprostokątnej do przeciwprostokątnej drugiego trójkąta, to te trójkąty są podobne. |
Można też rozpatrywać stosunki przeciwprostokątnych do odpowiednich przyprostokątnych.
OBWÓD TRÓJKĄTA
różnoboczny | równoranienny | równoboczny |
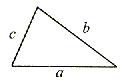 | 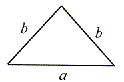 | 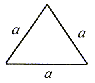 |
| L = a + b + c | L = a + 2b | L = 3a |
POLE TRÓJKĄTA
|
|
|
|
|
P = | P = | P = | P = | P = |
TWIERDZENIE PITAGORASA
 | Jeżeli trójkąt jest prostokątny, to suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. a2 + b2 = c2 |
TWIERDZENIE ODWROTNE DO TWIERDZENIA PITAGORASA
Jeżeli w trójkącie o bokach długości a, b i c zachodzi równość a2 + b2 = c2, to trójkąt jest prostokątny.
OKRĄG OPISANY NA TRÓJKACIE
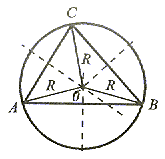 | Na każdym trójkącie można opisać okrąg. Środkiem okręgu opisanego jest punkt przecięcia się symetralnych boków trójkąta. |
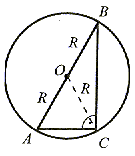 | Środek okręgu opisanego na trójkącie prostokątnym leży w połowie przeciwprostokątnej. |
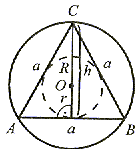 | Środek okręgu opisanego na trójkącie równobocznym i środek okręgu wpisanegow trójkąt równoboczny pokrywają się. |
Promień okręgu opisanego jest: R =
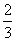 h.
h.Promień okręgu wpisanego jest: r =
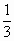 h.
h.Zależność między obydwoma promieniami: R = 2r.
Opracował: Krzysztof Leszczyński & Marta Sulowska
Źródło: matematyka.net
Licencja: Creative Commons - bez utworów zależnych

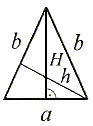
 h1
h1