Polak rozwikłał tajemnicę liczb pierwszych cz. 2 - Uniwersalny kod liczb odkryty

Przedstawiony kod liczb naturalnych ma co najmniej podobną wartość naukową w matematyce, jak okresowy układ pierwiastków Mendelejewa w chemii.

Uniwersalny kod liczb naturalnych został odkryty

Zanim przejdę do zasadniczego wątku chcę się odwołać do moich wcześniejszych artykułów pt. pt."Polak rozwikłał tajemnicę liczb pierwszych cz.1" (EIOBA, 11.03.2018), oraz "Liczby pierwsze, jedynka i grzebień" (EIOBA, 20.03.2018).

Przedstawiłem w tych publikacjach pogląd odmienny od obowiązującego w matematyce kanonu budowy liczb. Wykazałem, że elementarna budowa liczb naturalnych nie jest "atomowa", jak od stuleci przyjęło się uważać, ale krotnościowa, czyli że każda  liczba naturalna jest (wielo)krotnością/iloczynem jej najmniejszego dzielnika dzielącego ją bez reszty.  

Według tego nowego spojrzenia na liczby dla liczb pierwszych najmniejszym elementem iloczynu, który dzieli te liczby bez reszty, jest liczba 1. Podobnie dla każdej liczby parzystej liczba 2, dla liczb podzielnych przez trzy liczba 3, dla liczb podzielnych przez pięć liczba 5, dla liczb podzielnych przez siedem liczba 7, dla liczb podzielnych przez jedenaście liczba 11 itd.   

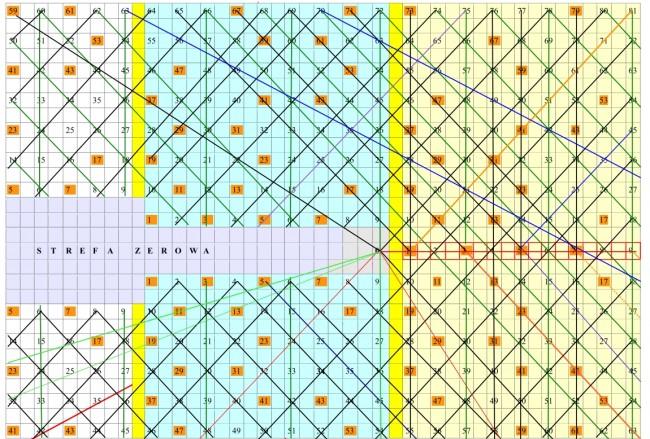
Wskazywałem w w/w artykułach na okoliczność, że liczba 1 jest liczbą pierwszą i że niesłusznie, i hamująco dla całej teorii liczb, została wykluczona z ich zbioru. O prawdziwości tego stwierdzenia można się naocznie przekonać na stworzonym przeze mnie schemacie uniwersalnego kodu liczb naturalnych (Rys. 1).

Niefortunnie, bo na podstawie błędnie przyjętego modelu budowy liczb umówiono się kiedyś w matematyce, że liczba 1 nie będzie zaliczana do zbioru liczb pierwszych. Powodem było to, iż przy błędnych założeniach o atomowej budowie liczb jedynka, jako liczba pierwsza, zakłócała wymóg jednoznaczności w takim (atomowym) ich przedstawianiu. Wobec tego, nie mając lepszego pomysłu na to, w jaki sposób jednoznacznie przedstawiać liczby, ułożono definicję, zwaną podstawowym prawem arytmetyki (lub inaczej; podstawowym twierdzeniem arytmetyki).

Mówi ona że:

                                               "każdą liczbę naturalną większą od 1,

                                                    nie będąca liczbą pierwszą,

                    można jednoznacznie przedstawić w postaci iloczynu liczb pierwszych"

            Jak widać; to usunięcie liczby 1 niewiele tu dało, bo powstałe na bazie tej amputacji prawo, będąc z pozoru matematycznie poprawnym, w istocie poprawnym nie jest. Nie dotyczy wszystkich liczb naturalnych, a tylko niektórych z nich. Nie zaprzecza logice jedynie w odniesieniu do obszaru sztucznie przyjętych ograniczeń, które w sobie zawiera. Stąd w istocie wszystko, co z tego twierdzenia wynika, ma jedynie pozory poprawności. Twierdzenie nie opisuje faktycznej budowy liczb naturalnych, ani wspólnego dla wszystkich bez wyjątku liczb klucza, decydującego o unikalności każdej z nich z osobna.

W gruncie rzeczy obowiązujące obecnie w matematyce podstawowe twierdzenie arytmetyki stwierdza włóaściwie jedynie to, że gdyby w zbiorze liczb naturalnych nie przeszkadzała obecność liczb pierwszych, liczby naturalne można by jednoznacznie przedstawiać w sposób, o jakim mówi to twierdzenie. 

Dokładnie mówiąc jest podwójnie błędne. Po pierwsze błędnie merytorycznie, bo nieprawdziwie opisuje rzeczywistość, a po drugie dlatego, że mieni się prawem podstawowym mimo, iż nie nie dotyczy wszystkich liczb naturalnych i nie funkcjonuje na poziomie ogólnym.

Odpowiednio; Wyklucza ze zbioru liczb pierwszych liczbę 1 i w konsekwencji fałszywie opisuje budowę liczb, oraz zawęża możliwość jednoznacznego ich przedstawiania tylko do większych od 1 i niepierwszych. Nazywanie prawem podstawowym definicji tak zawężonej i o tak rozbudowanej wybiórczości, jest nieporozumieniem.

Tradycyjna matematyka,  nazywając taką naciąganą definicję prawem podstawowym, nie tylko popełnia nadużycie, ale też sama się przyznaje, że nie wie jak liczby są zbudowane i tym samym jak jednoznacznie określać ich unikalność. Jednakże nawet teraz, kiedy już wiadomo jak liczby są zbudowane i według jakiej zasady rozpoznawać unikalność każdej z nich, tak zwana matematyka głównego nurtu nie chce przyjąć tego faktu do wiadomości. 

Oficjalna nauka, którą w Polsce reprezentuje zwłaszcza Polska Akademia Nauk, ignorując istnienie nowego, prawidłowego opisu budowy liczb oraz odkryć, które już dzięki niemu nastąpiły, działa nieracjonalnie i ze szkodą dla rozwoju wiedzy. Z pewnością za taką postawą PAN i i matematyków z pozostałych ośrodków naukowych nie stoją względy naukowe. 

Jest to postawa niewiarygodnie absurdalna, bo i tak nic przecież nie zmienia faktu - czy się to komuś podoba, czy nie - że powszechnie obecnie uznawane "podstawowe twierdzenie arytmetyki" nigdy nie opisywało właściwie budowy liczb i faktycznie nie miało rangi prawa podstawowego. Miało tą rangę tylko nominalnie, bo błędnie i na wyrost. Ma nazwę i miejsce w matematyce, na które nigdy nie zasługiwało, bo ani nie odzwierciedlało prawdy o budowie liczb, ani o tym, co stanowi o ich indywidualnej unikalności.

Prawdziwy matematyczny fakt jest taki, co opisuje nowo odkryte, właściwe tym razem, podstawowe prawo arytmetyki, że wszystkie liczby naturalne, bez żadnego wyjątku, są zbudowane według jednej, tej samej zasady. 

Reasumując; obowiązujące aktualnie w matematyce głównego nurtu podstawowe twierdzenie arytmetyki, jest niewiarygodnym, kompromitującym tę naukę bublem. Jakimś niezrozumiałym sposobem zostało powszechnie uznane za poprawne i przez prawie dwa pół tysiąca lat funkcjonuje jako jeden z kanonów matematyki. 

Słuszność powyższych krytycznych zastrzeżeń i stwierdzeń można sprawdzić na uniwersalnym układzie liczb naturalnych (rys.1).

Dokładnie na nim widać, jak liczby funkcjonują i jak układają się w ciągi. Widać że wszystkie są zbudowane według jednego wzorca, a unikalność każdej z nich wyrażana jest przez najmniejszy dzielnik danej liczby w parze z jej dzielnikiem największym. Iloczyn tych dwóch czynników daje wyłącznie tę jedną, unikalną liczbę. Ten dwuskładnikowy unikalny iloczyn, niepowtarzalny i jedyny w swoim rodzaju dla każdej liczby naturalnej, jednoznacznie i doskonale ją określa.

Opisuje ten stan nowe, tym razem poprawnie sformułowane podstawowe twierdzenie arytmetyki mające postać:

                              "Każdą liczbę naturalną, można jednoznacznie przedstawić

                                     w postaci unikalnego iloczynu dwóch liczb"

- Inaczej mówiąc w postaci iloczynu jej dzielników, z których jeden jest najmniejszym a drugi największym dzielnikiem tej liczby.

Sprowadzając powyższe prawo do twierdzenia najbardziej ogólnego stwierdzamy że:

                                          "Każda liczba naturalna jest krotnością jakiejś liczby naturalnej"

Jak można zauważyć; ta najbardziej ogólna i jednocześnie najbardziej uniwersalna postać definicji opisuje, nieznaną dotąd naturę liczb i ich rzeczywistą budowę. Jest dla teorii liczb definicją podstawową i kluczową. Pokazuje czym są liczby i jak je w związku z tym traktować i poznawać.

Kolejnym uszczegółowieniem tej definicji jest sformułowanie mówiące że:

                                   "Każda liczba naturalna jest krotnością jakiejś liczby pierwszej" ,

natomiast w następnej kolejności będzie stwierdzenie jeszcze bardziej szczegółowe mówiące że:  

             "Każda liczba naturalna jest krotnością jakiejś liczby pierwszej, zwanej/będącej liczbą macierzystą tej liczby"

Wynika stąd prawidłowość, że:

 Liczby mające różne liczebniki lecz tę samą liczbę macierzystą, należą zawsze do tego samego ciągu liczbowego. 

Nowe, podstawowe prawo arytmetyki, wyrażone zarówno w wersji uszczegółowionej, jak i w każdej wersji bardziej lub mniej ogólnej, jest w pełni uniwersalne. Jest prawdziwe dla wszystkich liczb bez wyjątku, w tym dla liczby 1 która, jako podstawowa, jest sama dla siebie jednocześnie dzielnikiem najmniejszym i największym.

Za pomocą iloczynu dwóch dzielników doskonale spełniony jest warunek jednoznaczności w przedstawianiu dowolnej liczby naturalnej. 

Nawiasem mówiąc; takie przedstawienie każdej liczby naturalnej stwarza między innymi możliwość unikalnego i jednoznacznego usytuowania jej również w układzie współrzędnych, co pośród wielu możliwości, jakie się dzięki nowemu prawu otworzyły, daje nowe pole do badań także z tej strony.

Łatwo zauważyć, i to jest konkluzją wieńczącą wyżej opisany stan rzeczy, że największym przełomem w obowiązujących dotychczas podstawach teorii liczb, jest zlikwidowanie podziału na liczby złożone oraz na liczby pierwsze - jako rzekomo niezłożone. Podział ten od początku był nielogiczny i błędny.

W rzeczywistości o złożoności liczb naturalnych i zajmowanym przez nie miejscu w ich świecie, nie decyduje suma pomniejszych liczb, z jakich się one składają, ale tworzące je iloczyny.

W rzeczywistości wszystkie liczby naturalne, włącznie z liczbami pierwszymi, są liczbami złożonymi, ponieważ każda liczba zbudowana jest podobnie, czyli z pewnej charakterystycznej dla niej ilości jednakowych elementów. Ściślej; z krotności jakiejś liczby pierwszej. To właśnie wyraża unikalny iloczyn dwóch dzielników danej liczby.

Mówiąc obrazowo; dzielnik najmniejszy danej liczby (i jednocześnie operator w arytmetycznym ciągu liczbowym tworzącym tę liczbę), to element budulca, konkretnej znormalizowanej "cegły" z której liczba jest "zrobiona", natomiast dzielnik największy, czyli liczebnik, to liczba wskazująca z ilu takich elementów liczba ta się składa.

Liczby pierwsze tworzą zbiór - tworząc niejako katalog tych "cegieł' - i z nich to właśnie zbudowane są wszystkie liczby. Cechą liczb naturalnych jest to, że każda z nich składa się z odpowiedniej ilości jednego tylko typu "cegieł", zwanych liczbami macierzystymi, lub też w zależności od potrzeby, operatorami. 

I o ile operator zawsze jest liczbą pierwszą, to liczebnik, w zależności od rodzaju liczby - czyli w zależności od tego czy  jest ona liczbą pierwszą, czy nie - może nią być, lub nie.

Jedynie gdy mamy do czynienia z liczbami pierwszymi; liczebnik liczby pierwszej zawsze jest liczbą pierwszą, a operator zawsze jest liczbą 1.

Generalnie:  Wszystkie liczby naturalne są zbudowane z liczb pierwszych, a te, które są zbudowane z tych samych liczb pierwszych (czyli mają tę samą liczbę macierzystą) należą do tego samego ciągu liczbowego. 

Bo, jak wyżej zostało powiedziane; każda liczba naturalna jest liczbą złożoną, składającą się z krotności jakiejś liczby pierwszej, będącej dla niej liczbą macierzystą.

Dopiero wychodząc od tego faktu, można w dalszej kolejności przyjąć kolejne podziały na liczby parzyste i nieparzyste, pierwsze i niepierwsze, dwudzielne i wielodzielne, podzielne przez konkretne liczby itd. itp.

Najważniejszym jest jednak fakt zdefiniowania czym w ogóle liczby są. Wiemy też dlatego, że liczby pierwsze, to liczby zbudowane wyłącznie z liczby 1, pomnożonej przez inną liczbę pierwszą, czyli podzielną tylko przez 1.

Zdanie sobie sprawy z tego prostego faktu pozwala na logiczne poruszanie się w świecie liczb, w tym liczb pierwszych.

Powyższe uporządkowanie pojęć ujawnia kolejną prawidłowość, że

       "każda liczba naturalna źródłowo należy do jednego i tylko jednego nieskończonego ciągu liczbowego, którego unikalne cechy wyraża jej najmniejszy dzielnik, będący liczbą pierwszą i jednocześnie liczbą macierzystą tego ciągu, czyli jego różnicą"

Znając unikalne, iloczynowe współrzędne każdej liczby naturalnej, a zatem i to, do którego ciągu ona należy, możemy zidentyfikować unikalne i jedynie dla niej przeznaczone miejsce, które zajmuje w całym świecie liczb, czyli w ściśle uporządkowanej strukturze ciągów liczbowych.  Wizualnie obrazuje tę sytuację uniwersalny układ liczb naturalnych, przedstawiony w tekście poniżej na rys.1. 

Reasumując: Znając już obecnie prawdziwą budowę liczb i miejsce każdej, wśród wszystkich innych, możemy w sposób logiczny i pewny, rozpracowywać prawidłowości rządzące liczbami, oraz panujące między nimi zależności.

Jest to zupełnie nowa możliwość, bo odkąd istnieją nauki matematyczne z powodu zakorzenionych błędów, takich możliwości i o takim potencjale poznawczym w dziedzinie liczb naturalnych, dotąd nie było. Nastąpił przełom, który w przeciągu kilku miesięcy umożliwił mi dokonanie większej ilości odkryć z zakresu wiedzy o liczbach pierwszych, niż miało to miejsce w całej światowej matematyce na przestrzeni ostatnich stu lat. I żeby nie być gołosłownym, zostało to wypunktowane w tekście poniżej.

Zważywszy, że w dodatku odkrycia te dokonane zostały przeze mnie w ciągu niespełna roku, jednoosobowo i jedynie z pomocą komputera osobistego, można wyrobić sobie pojęcie o skali możliwości, jakie otwierają na nowo sformułowane podstawy teorii liczb, oraz nowo odkryty uniwersalny układ liczb naturalnych. Ponadto, co istotne i wielce obiecujące, otworzyła się dzięki niemu olbrzymia ilość zupełnie nowych ścieżek badawczych, a ich ilość rośnie w miarę odkryć, które te badania przynoszą.

Ten uniwersalny układ daje nowe i szerokie możliwości zwłaszcza naukowcom wyposażonym w najnowocześniejszy sprzęt i zaawansowane, specjalistyczne programy informatyczne. Kwestia tylko w tym, czy korzystanie z niego przez tradycyjną naukę - a z pewnością już ma to miejsce - będzie uczciwe. Innymi słowy; czy naukowcy pracując i dokonując nowych odkryć, na bazie mojego uniwersalnego układu liczb naturalnych i moich dotychczasowych oraz przyszłych odkryć, będą się do tego przyznawać, czy dalej będą udawać, że o niczym takim nie wiedzą i z moich prac nie korzystają.

Nawiasem mówiąc; w dniu 2 października 2018 r. przesłałem polskiemu środowisku naukowemu, z Polską Akademią Nauk i kilku uniwersytetami włącznie, opis i schemat odkrytego przeze mnie uniwersalnego układu liczb naturalnych, wraz z prezentowanymi poniżej rysunkami 1, 2 i 3. 

Dodam, że zgłoszenie tego odkrycia nie spotkało się z jakimkolwiek odzewem, podobnie jak zgłoszenia innych moich odkryć posyłanych do tych instytucji, począwszy od stycznia 2018 roku.

Swoją drogą milczenie środowiska naukowego jest dość dziwne zważywszy, że odkryty przeze mnie i zgłoszony kod -układ liczb naturalnych, jest absolutnie matematycznie poprawny i skuteczny, oraz ma w dodatku co najmniej podobny potencjał w teorii liczb i matematyce w ogóle, jak okresowy układ pierwiastków Mendelejewa w chemii. Jeśli wierzyć w to, jak określano taki, wcześniej jedynie teoretyczny, oczekiwany przez ponad dwa tysiąclecia układ, odkrycie go, jest odkryciem epokowym. Z bliżej nie znanych mi przyczyn jednocześnie odkryciem ignorowanym przez polską, instytucjonalną matematykę i nie wiedzieć czemu ukrywanym przez nią, przed światem.

Trudno stwierdzić czemu ma to służyć zwłaszcza, że uniwersalny układ liczb naturalnych, jak wyżej wspomniałem, już we wstępnych analizach dał dużo różnych i nieznanych wcześniej informacji.

Przechodząc do meritum;

Na planszy (Rys.1) układ ten, który w rzeczywistości jest trójwymiarowy, sferyczny, nieskończony, z punktem zerowym w środku, pokazany jest w formie dwuwymiarowej, jako płaski schemat, mający nieporównanie mniejsze możliwości od oryginału, ale też dający się w nieskończoność rozbudowywać we wszystkich kierunkach i nawet w wersji dwuwymiarowej pozwalający operować na dowolnie wielkich liczbach.

Oto niektóre informacje o budowie i funkcjach układu w wydaniu dwuwymiarowym;

1. Punktem centralnym całego układu, jest punkt zerowy pierwszego sektora (kolor seledynowy) znajdujący się w pobliżu kolumny komórek zaznaczonej kolorem żółtym .

2. Punkt zerowy jest punktem początkowym nieskończenie rozległej strefy zerowej, w której (poza zerem) nie ma innych liczb.

3. Kolejne sektory i ich punkty zerowe "przyrastają" w nieskończoność zarówno w lewą jak i prawą stronę układu, lecz tylko po lewej stronie od punktu zerowego tworzy się tzw. "strefa zerowa". Na prostej w prawo od centralnego punktu zerowego przyrastają liczby od zera do nieskończoności. Kolejne, pionowo w górę i w dół oraz na wszystkie strony rozprzestrzeniające się liczby tworzą sektory od 1 do 9 w systemie dziewiątkowym. Początkiem każdego sektora jest szereg  liczb zaczynający się od 1 do 9, następnie od 10 do 18, od 19 do 27 itd.

4. Podobne sektory, idące w górę i w dół, zaznaczone pionowymi liniami żółtych komórek, tworzą liczby usytuowane na lewo od punktu zerowego z tym, że są przedzielone strefą zerową.  

5. Linie przecinające układ prostopadle i skośnie łączą liczby tworzące wszelkie możliwe, nieskończone ciągi liczbowe. Ciągi te dają się wyznaczyć zarówno w  poszczególnych sektorach, jak w wersji gdy linie łączące punkty na prostej zerowej, w miejscach stacjonowania w/w liczb, są liniami granicznymi kolejnych sektorów. Zarówno w pierwszym, jak i w drugim przypadku, wszystkie sektory indywidualnie, jak i w połączeniu ze sobą, mogą wykonywać podobne operacje, na coraz większych liczbach.Wszystkie sektory ze wszystkimi są kompatybilne i doskonale, wzajemnie się przenikają i uzupełniają.

6. Rozbudowywany bez ograniczeń układ obejmuje wszystkie liczby naturalne od zera do nieskończoności i uwidacznia wszelkie zależności między nimi. 

7. Układ wskazuje, że wszystkie liczby są unikalnymi indywidualnościami zajmującymi własne i jedynie właściwe dla siebie miejsca.

8. Wszystkie, bez wyjątku, liczby układu są ze sobą powiązane właściwymi sobie, logicznymi, systemowymi zależnościami.

9. Liczby należące do określonych rodzajów i grup zajmują miejsca odpowiadające punktom na prostych zmierzających do nieskończoności, tworząc na nich w sumie wszystkie możliwe ciągi liczbowe.

10. Liczby znajdujące się na tych samych prostych – należące do tych samych ciągów - są krotnościami liczb macierzystych większych od zera, stojących na początku ciągów.

11. Jeśli jakaś zależność/ zasada liczbowa działa w jakimkolwiek wycinku układu, działa w całym układzie.

Rys. 1. Uniwersalny układ liczb naturalnych

• Co można odczytać z uniwersalnego układu liczb naturalnych?

  Oto ciekawsze informacje:

  • na planszy kodu (Rys.1) widać, że ciągi liczbowe mogą być wyprowadzane od wszystkich liczb. Liczby leżące na jednej, dowolnej linii, zawsze tworzą ciąg arytmetyczny. Rzeczywisty początek ciągu daje leżąca na tej linii najmniejsza liczba, będąca jednocześnie jego różnicą. Jeśli jest ona liczbą pierwszą, jest to tak zwana liczba macierzysta.

  • kod ujawnił, że istnieją cztery główne ciągi liczbowe dla liczb pierwszych (oznaczone na planszy pomarańczowymi liniami przerywanymi). Mają postać n+10, a ich liczbami macierzystymi n, tj. od których te ciągi się zaczynają, są liczby 1, 3, 7 i 9. Przez te cztery zbiory sprzężone wspólną formułą n+10, są generowane wszystkie bez wyjątku liczby pierwsze od 1 do nieskończoności. Ciągi te, chociaż nie są ciągami najbardziej zasobnymi w liczby pierwsze, zyskały taki status dlatego, że jest to jedyny istniejący w świecie liczb zestaw ciągów liczbowych rozdzielający je według cyfr stojących na końcach generowanych liczb, czyli cyfr 1, 3, 7 i 9.  Inne końcówki cyfrowe, wśród liczb pierwszych, wszakże nie występują

  • kod przyniósł m.in. rozstrzygnięcie popularnej i nierozwiązanej wcześniej hipotezy zawierającej się w pytaniu: "czy dla wyrażenia n²+1, gdzie n jest liczbą parzystą, istnieje nieskończona ilość rozwiązań w postaci liczby pierwszej?"

    Odpowiedź brzmi: TAK. Dowodem na to jest arytmetyczny ciąg liczbowy (n+42)²+1, w którym liczbę n daje zwykły ciąg arytmetyczny, dla którego liczbą początkową jest 0 a operatorem 42. Poszczególne składniki tego ciągu, po podniesieniu do kwadratu i dodaniu do nich liczby 1, dają ciąg o relatywnie dużym i dość stałym zagęszczeniu liczb pierwszych, gdzie statystycznie więcej niż co siódma liczba ciągu jest liczbą pierwszą. Odliczając dodatkowo naocznie rozpoznawalne liczby podzielne przez 5, statystyka ta poprawia się jeszcze o około 40% i w efekcie prawie co czwarta liczba tego, tak oczyszczonego ciągu,  jest liczbą pierwszą.

W miarę operowania na coraz większych liczbach częstotliwość liczb pierwszych w ciągu tym nie spada, a przynajmniej taką cechę daje się stwierdzić dla liczb do wielkości stu miliardów.

        Daje się też zauważyć w nim znaczną regularność sekwencyjnego występowania liczb pierwszych.

Specyficzne cechy tego ciągu nie biorą się z przypadku. Wszystkie liczby nieparzyste z których uzyskuje się w nim ich kwadraty, są liczbami bardzo specyficznymi. Każda z tych liczb stoi na schemacie (rys.1) w wyjątkowym, węzłowym miejscu, w którym krzyżują się wszystkie rodzaje linii podstawowej siatki wykluczeń, czyli liczb podzielnych jednocześnie przez 2, 3 i 7.

Osobna, dodatkowa i oczywista eliminacja z ciągu rozpoznawalnych naocznie liczb podzielnych przez 5 sprawia, że statystyka zagęszczenia liczb pierwszych odpowiednio się poprawia. W sumie, z nieskończonego zbioru wszystkich liczb naturalnych, wyeliminowanych jest wówczas ponad 80% liczb, które z definicji nie mogą być liczbami pierwszymi.

          Oznacza to, że w pozostałych niecałych 20 procentach liczb, pośród których działa ciąg (n+42)²+1, skumulowanie są wszystkie możliwe liczby pierwsze i siłą rzeczy musi się to odbijać na ich zwiększonym zagęszczeniu w tymże ciągu. Jest nie wykluczone i raczej pewne - chociaż jeszcze wymaga dokładniejszego sprawdzenia - że spośród wszelkich możliwych ciągów arytmetycznych, mogących działać w tych specyficznych 20-tu procentach liczb, zawierających wszystkie liczby pierwsze, ciąg (n+42)²+1, jest ciągiem najbardziej w nie bogatym.

Reasumując: Zważywszy że ciąg ten, aż do wielomiliardowych wartości regularnie, licznie oraz ze stałą częstotliwością i w bardzo zawężonym obszarze liczbowym generuje liczby pierwsze, byłoby bezsensem przyjmować iż mógłby w jakimś momencie przestać funkcjonować w typowy dla siebie sposób i przestać je generować. Gdyby chcieć jakkolwiek zakwestionować stałość zachowywania się ciągów liczbowych, trzeba by najpierw odpowiedzieć na pytanie: gdzie indziej i dlaczego wszystkie regularnie generowane liczby pierwsze w danym ciągu miałyby się podziać?  Z jakiej przyczyny miałyby się gdzieś w ogóle przenosić, i to w dodatku do ciągów teoretycznie mniej sprzyjających ich występowaniu? 

Biorąc pod uwagę powyższe logika nakazuje wniosek, że już samo istnienie ciągów liczb parzystych, w których kwadraty +1 niektórych liczb dają liczby pierwsze, jest wystarczające by stwierdzić, że ilość liczb pierwszych dla n²+1, gdzie n jest liczbą parzystą, jest nieskończona. 

• Dla pokazania  jednej z wielu przydatności kodu chciałbym posłużyć się przykładem tego, w jaki sposób przy jego wykorzystaniu można zrealizować i jednocześnie zilustrować wizualnie poszukiwanie liczb pierwszych.

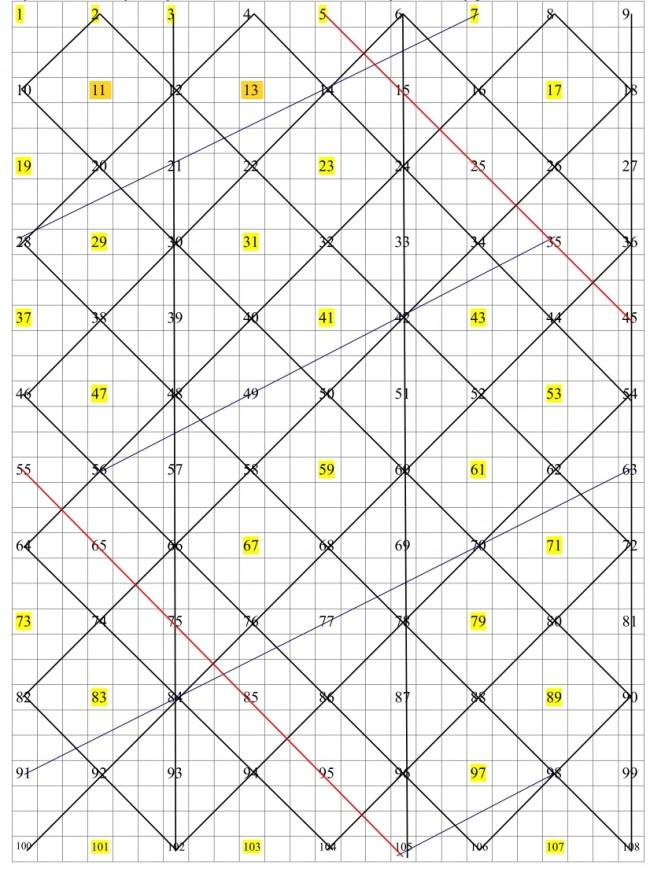
Posłużą do tego Rysunki 2 i 3

Rys. 2 poniżej pokazuje tzw. fazę podstawową wykresu. Ilustruje sposób używania schematu do znajdowania liczb pierwszych z użyciem tylko jednego sektora. Linie pionowe wykluczają liczby podzielne przez 3, natomiast skośne tworzące romby liczby podzielne przez 2. Czerwone linie wykluczają liczby podzielne przez 5 a niebieskie przez 7. Jest to tak zwana podstawowa siatka wykluczeń. Liczby niewykluczone, oznaczone kolorem żółtym, to liczby pierwsze.

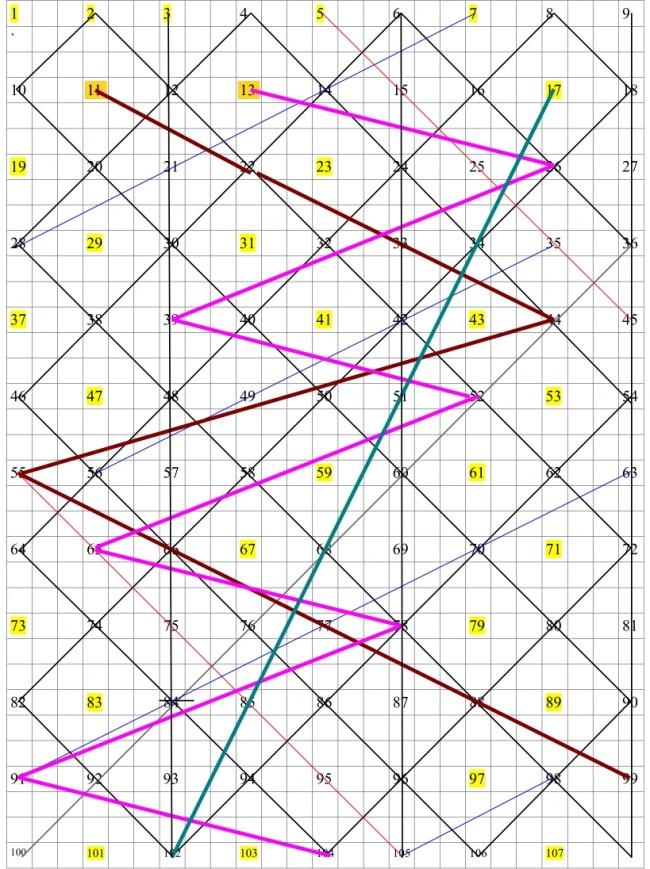
Rys.3 Wykluczanie większych liczb niepierwszych polega na nakładaniu na siatkę podstawową linii łączących wielokrotności kolejnych liczb pierwszych większych od 10 – tutaj poglądowo 11,13,17

Jak widać na rysunku przebadanie w podany sposób zbioru liczb naturalnych wyklucza wszystkie liczby z wyjątkiem liczb pierwszych, czyli wskazuje które liczby są liczbami pierwszymi.

Oczywiście w praktyce nie ma potrzeby pracować na takim zagęszczeniu linii, ponieważ każą z nich można wygodnie poprowadzić w zupełnie osobnym, dowolnie wybranym i równoważnym pod każdym względem sektorze, względnie alternatywnie można przyjąć metodę linii prostych i pracować na schemacie wielosektorowym (Rys.1), co umożliwia układ kodu.

Linie wielokrotności poszczególnych liczb (w tym wypadku liczb pierwszych) nie będą przy metodzie linii prostych łamane, ale proste. Będą one w sposób spójny z całym układem przecinać sąsiednie sektory i funkcjonować z identycznym, doskonale poprawnym skutkiem matematycznym - tak jak funkcjonuje cały kod.