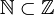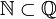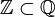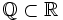Zbiór liczb naturalnych
Liczb naturalnych używamy do określenia ile jest osób w jakimś miejscu, do ustalania kolejności, ile sztuk czegoś mamy itp. Mówiąc o liczbach naturalnym mamy na myśli liczby należące do zbioru 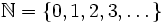 . Jednym z podzbiorów liczb naturalnych jest zbiór liczb naturalnych dodatnich, które oznaczamy
. Jednym z podzbiorów liczb naturalnych jest zbiór liczb naturalnych dodatnich, które oznaczamy 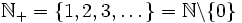 .
.
 | DEFINICJA Zbiorem liczb naturalnych nazywamy zbiór |
Podzbiorami liczb naturalnych jest zbiór liczb pierwszych i zbiór liczb złożonych.
Zbiór wszystkich liczb pierwszych czasami jest oznaczany przez 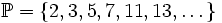 , a i-ta liczba pierwsza przez pi np. p3 = 5.
, a i-ta liczba pierwsza przez pi np. p3 = 5.
Zbiór liczb całkowitych
 | DEFINICJA Zbiorem liczb całkowitych nazywamy zbiór |
Ponadto zbiór liczb całkowitych możemy podzielić na dwa podzbiory -- zbiór liczb całkowitych dodatnich i zbiór liczb całkowitych ujemnych. Zbiór liczb całkowitych dodatnich oznaczamy przez 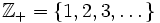 , natomiast zbiór liczb całkowitych ujemnych przez
, natomiast zbiór liczb całkowitych ujemnych przez 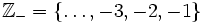 . Łatwo zauważyć, że
. Łatwo zauważyć, że 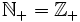 .
.
W polskiej literaturze czasami można się spotkać z oznaczeniem zbioru liczb całkowitych poprzez 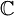 (jednak nie jest on znanym, międzynarodowym oznaczeniem, dlatego też nie będziemy korzystać z niego w tej książce).
(jednak nie jest on znanym, międzynarodowym oznaczeniem, dlatego też nie będziemy korzystać z niego w tej książce).
Zbiór liczb wymiernych
 | DEFINICJA Zbiór liczb wymiernych jest to zbiór wszystkich liczb, w których każdą liczbę można zapisać w postaci ułamka zwykłego |
Podobnie jak to było w zbiorze liczb całkowitych, zbiór liczb wymiernych dodatnich oznaczamy przez 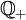 , a ujemnych przez
, a ujemnych przez 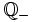 .
.
W niektórych polskich książkach zbiór liczb wymiernych jest oznaczany przez 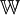 .
.
Zbiór liczb niewymiernych
 | DEFINICJA Zbiór liczb niewymiernych jest to zbiór tych liczb rzeczywistych, które nie są wymierne tzn. tych, których nie można zapisać w postaci ułamka zwykłego |
Zbiór liczb niewymiernych nie ma ogólnie przyjętego międzynarodowego oznaczenia. Możemy go zapisać wykorzystując polskie oznaczenie 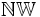 (które nie jest wykorzystywane na całym świecie), czy też jako różnicę zbioru liczb rzeczywistych i zbioru liczb wymiernych:
(które nie jest wykorzystywane na całym świecie), czy też jako różnicę zbioru liczb rzeczywistych i zbioru liczb wymiernych: 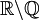 .
.
Przykładem liczby niewymiernej może być liczba 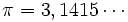 , czy też
, czy też 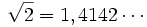 .
.
Zbiór liczb rzeczywistych
 | DEFINICJA Zbiór liczb rzeczywistych jest sumą zbiorów liczb wymiernych i zbioru liczb niewymiernych. |
Zbiór liczb rzeczywistych dodatnich oznaczamy przez 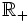 , a ujemnych przez
, a ujemnych przez 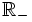 .
.
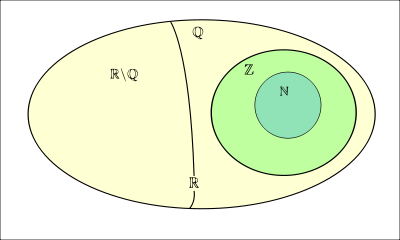
Pomiędzy liczbami naturalnymi, całkowitymi, wymiernymi i niewymiernymi możemy zaobserwować poniższe związki:
Rozwinięcie dziesiętne
Rozwinięcie dziesiętne części liczb rzeczywistych może być skończone np. 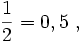
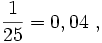
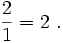 Jednak nie wszystkie liczby cechuje ta własność.
Jednak nie wszystkie liczby cechuje ta własność.
Przyjrzyjmy się bliżej liczbie 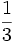 . Na pewno pamiętamy, że
. Na pewno pamiętamy, że 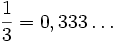 . Aby otrzymać rozwinięcie dziesiętne danej liczby, po prostu wykonujemy zwyczajne dzielenie. Ale jak przejść z rozwinięcia dziesiętnego na postać ułamka? Zobaczmy:
. Aby otrzymać rozwinięcie dziesiętne danej liczby, po prostu wykonujemy zwyczajne dzielenie. Ale jak przejść z rozwinięcia dziesiętnego na postać ułamka? Zobaczmy:
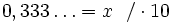

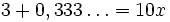 , ponieważ
, ponieważ 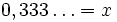
- 3 + x = 10x
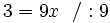
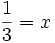
Otrzymaliśmy oczekiwany wynik.
Innym przykładem, trochę trudniejszym jest 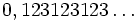 . Wprawni weterani mogą się domyślać, że będzie ona równa
. Wprawni weterani mogą się domyślać, że będzie ona równa 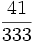 . Zobaczmy na rozwiązanie:
. Zobaczmy na rozwiązanie:

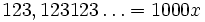 , ponieważ
, ponieważ 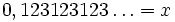
- 123 + x = 1000x
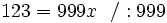
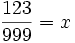
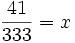
Szukaną liczbą jest 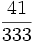 .
.
Liczbę 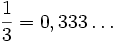 możemy zapisać także w formie
możemy zapisać także w formie 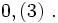 Podobnie
Podobnie 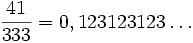 możemy zapisać jako
możemy zapisać jako 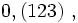 a także
a także  W takiej formie możemy zapisać dowolną liczbę o rozwinięciu dziesiętnym okresowym.
W takiej formie możemy zapisać dowolną liczbę o rozwinięciu dziesiętnym okresowym.
Nie wszystkie liczby rzeczywiste można zapisać w postaci rozwinięcia dziesiętnego skończonego, czy też nawet rozwinięcia nieskończonego okresowego. W takiej formie można zapisać wszystkie liczby wymierne, natomiast nie możemy zapisać w ten sposób rozwinięcia liczby niewymiernej. Przykładem liczby niewymiernej może być liczba Eulera 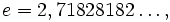 a także liczba
a także liczba 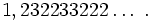 Jak widać, nie są one liczbami okresowymi.
Jak widać, nie są one liczbami okresowymi.
Treść udostępniana na licencji GNU Free Documentation License . Źródło: Wikibooks.pl
Autor: Wikibooks

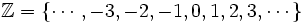 .
. , gdzie
, gdzie 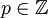 i
i 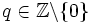 .
.