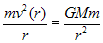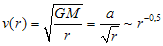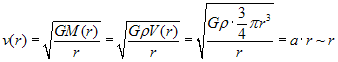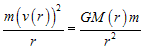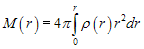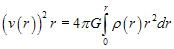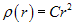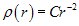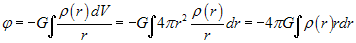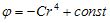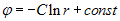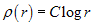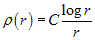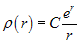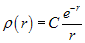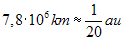Wstęp
Jedną z konsekwencji prawa odwrotnej proporcjonalności siły grawitacji do kwadratu odległości jest taka własność pola grawitacyjnego, że siła działająca na próbną masę punktową m w odległości r od środka cienkiej jednorodnej powłoki kulistej o promieniu R i masie M jest dla punktów leżących na zewnątrz powłoki (r > R) dokładnie taka, jakby cała masa powłoki była skupiona w jej środku. Natomiast wewnątrz powłoki (r < R) siła grawitacji nie występuje. Różne są sposoby dowodzenia tych twierdzeń; od czysto formalnych (całki), przy pomocy szeregów [1], a skończywszy na intuicyjnych, zakładających, że fragment powłoki kulistej jest zawsze regularną czaszą, niezależnie od położenia rozpatrywanego punktu.

Korzystając ze wspomnianej własności spróbujemy - w sposób dostępny dla ucznia - znaleźć kształt potencjału dla różnych rozkładów gęstości materii wewnątrz kuli. Dla Ziemi będzie to rozkład jednorodny (uśredniony), a np. dla jądra Galaktyki już nie. Mogłoby się wydawać, że traktowanie Ziemi czy galaktyk jako wydrążonej kuli jest sprawą czysto akademicką. Ale tak przecież postępował Izaak Newton, który w swoich Principiach rozpatrywał przypadek "pustej Ziemi", a następnie pełnej jednorodnej kuli, działającej na masę umieszczoną w jej wnętrzu. Problemem tym również zajmował się Leonard Euler, choć wnioski jakie formułował, nie do końca były precyzyjne [2].
Tytuł artykułu nawiązuje do potencjału grawitacyjnego, który określa rozkład mas (lub gęstości) danego układu fizycznego, względem wybranego układu współrzędnych (płaskiego lub przestrzennego). W niniejszej pracy ograniczymy się do obiektów astronomicznych o symetrii sferycznej.
Do lat osiemdziesiątych XX w. przyjmowano następujący rozkład mas w Galaktyce:- łączna masa 11 • 1011 mas Słońca, tj. 2,1 • 1045 kg, promień 36 kiloparseków (kpc), grubość 1 kpc,
- zagęszczenie (bulge) centralne o masie 1,4 • 1010 mas Słońca i promieniu 120 pc,
- jądro o średnicy ok. 120 pc i masie 5 • 109 mas Słońca,
- dysk o masie 1,3 • 1011 mas Słońca, promieniu 6 kpc i grubości 0,5 kpc,
- sferyczne halo o masie 2 • 1011 mas Słońca i promieniu 50 kpc.Bardzo zróżnicowany jest również rozkład gęstości:
- średnia gęstość całej Galaktyki:
0,1 • Mo pc3 - w sąsiedztwie Słońca:
0,1 • Mo pc3 - w odległości 100 pc od Centrum:
100 • Mo pc3 - w odległości 10 pc od Centrum:
7000 • Mo pc3 - w odległości 1 pc od Centrum:
400000 • Mo pc3 gdzie: Mo - masa Słońca, pc (parsek - 3,086 • 1016 m).
Widzimy tutaj bliską analogię do Układu Słonecznego. Słońce zawiera w sobie 99,866% masy zawartej w ciałach Układu Słonecznego (bez gazu i pyłu międzygwiezdnego), tzn. skupia 99,87% masy całego układu. Rozmiary układu Słonecznego mierzone promieniem orbity Plutona wynoszą 12 mld km (80 j. a.), a promień Słońca 696 tys. km czyli 1,4 • 10-5 - w grubym przybliżeniu jedna milionowa całkowitych rozmiarów Układu [3].
0znaczmy przez M masę Słońca i potraktujmy ją jako masę punktową, a przez m - masę dowolnej planety naszego układu, przyjmując, że poruszają się one po orbitach kołowych. Z warunku równowagi siły dośrodkowej i siły grawitacji mamy:
(1)
, stąd (2)Zależność tę ilustruje poniższa tabela i rys. 1a
Planeta Merkury Wenus Ziemia Mars Jowisz Saturn Uran Neptun Pluton Odległość [AU] 0,387 0,723 1,000 1,540 5,203 9,539 19,18 30,058 39,75 Promień orbity
(średni) [mln km]57,9 108,2 149,5 227,9 778,0 1427,0 2870,0 4497,0 5947,0 Prędkość orbitalna
(średnia) [km/s]47,8 25,0 29,0 24,1 13,1 9,7 6,8 4,4 4,7
Rys.1 a) b) Przyjmijmy teraz, że rozmiary Słońca nie są zaniedbywalne; rozpatrzmy punkt położony wewnątrz jednorodnej kuli (o luźnej strukturze) w odległości r od jej środka. Masa oddziaływującą grawitacyjnie jest zawarta w sferze o promieniu r, zatem:
Otrzymujemy proporcjonalną zależność między prędkością, a odległością od środka Słońca (Rys.1b).
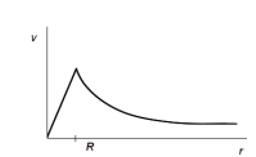
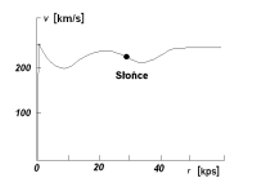
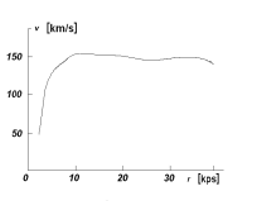
Oczekiwano podobnej zależności dla galaktyk, nawet, jeżeli rozkład gwiazd jest raczej chmuro-podobny (cloud-like), a nie dokładnie sferyczny. Wykorzystując nowoczesne metody pomiarów astrofizycznych (przesunięcie dopplerowskie linii spektralnych (gwiazdy), obserwacje radioastronomiczne neutralnego wodoru (21cm), a ostatnio również obserwacje wodoru zjonizowanego i linii absorpcyjnych gorącego gazu w zakresie optycznym) stwierdzono, że gwiazdy na brzegu galaktyk poruszają się szybciej niż oczekiwano. Pozwoliło to na sporządzenie tzw. krzywej rotacji, czyli zależności prędkości gwiazdy w odległości od centrum galaktyki. Astronomowie nazywają to zjawisko spłaszczeniem krzywej rotacji galaktyki (flat rotation curve) (Rys.2b) . W chwili obecnej dla najbliższych galaktyk spiralnych wyznaczono już dokładnie krzywe rotacji. Rys. 2a, b przedstawią zależności v = f(r) dla Drogi Mlecznej i galaktyki NGC 3198 [4], [5].
Zatem model rotacji Galaktyki jest niezgodny z obserwowanym obrotem galaktyk a twierdzeniami aktualnych teorii fizycznych. Próby rozwiązania problemu rotacji Galaktyki zawierają w sobie hipotezę ciemnej materii, znanej jako Zmodyfikowana Dynamika Newtona.
Skomplikowany wykres rotacji Galaktyki jest spowodowany złożoną budową naszej Galaktyki (typ morfologiczny - galaktyka spiralna), głównie niejednorodnym rozkładem przestrzennym materii gwiazdowej i międzygwiazdowej. Biorąc pod uwagę rozkład mas i prędkości, gęstość przestrzenną i jej gradient możemy wyróżnić w budowie galaktyki spiralnej z grubsza następujące składowe:
- podsystemy płaskie (dysk z ramionami),
- podsystemy sferyczne (jądro, halo galaktyczne).Ruchy gwiazd w galaktykach są określone nie przez oddziaływania dwuciałowe (jak to ma miejsce np. dla cząsteczek gazu), ale przez wypadkowe pole grawitacyjne wytworzone przez całkowitą masę układu. Z analizy prędkości przestrzennych gwiazd wynika, że wszystkie obiekty Galaktyki obiegają jej środek (środek masy układu); obiekty należące do różnych podsystemów wykazują jednak odmienne cechy kinematyczne.
Rys.2 a) b) Ciała podsystemu płaskiego poruszają po orbitach niemal kołowych, z dużymi, niewiele różniącymi się od siebie prędkościami (mała dyspersja prędkości). Obiekty podsystemów sferycznych poruszają się po nieuporządkowanych orbitach eliptycznych (keplerowskich), prędkości są niewielkie, a dyspersja prędkości - duża. Prędkości obiegu dla podsystemu płaskiego zależą od odległości od środka Galaktyki (rotacja różniczkowa).
Z dydaktycznego punktu widzenia korzystne - jak się wydaje - byłoby rozpatrzenie pewnych dynamicznych modeli ruchu obrotowego galaktyk, ponieważ rozkład prędkości gwiazd w Galaktyce ma duże znaczenie kosmologiczne. Gwiazdy obiegające środek galaktyki mają zbyt duże prędkości, niżby to wynikało z obliczeń opartych na newtonowskiej teorii grawitacji. Nasuwa się tutaj pewna analogia; jeżeli popatrzymy na Układ Słoneczny jako całość, to prędkości planet maleją wraz ze wzrostem odległości od Słońca. Łatwo to możemy sprawdzić na lekcjach astronomii w dziale Astronomia i grawitacja. Tymczasem prędkości gwiazd dla większości obserwowanych galaktyk spiralnych wraz ze wzrostem odległości od centrum ruchu są mniej więcej stałe, a nawet się zwiększają (!). Ale dla gwiazd w Galaktyce obliczenia wykonywano dla masy świecącej materii. To sugeruje z kolei, że materia rozproszona w naszej Galaktyce zawiera jakiś ciemny składnik (halo galaktyczne). Szacuje się, że masa tego składnika jest około 10 razy większa niż masa wszystkich widocznych gwiazd. Astrofizycy powiadają, że 90% masy Galaktyki ”grawituje”, a tylko 10% ”świeci” [6].
Zacznijmy od najczęściej spotykanych modeli [7]:
(3)
a) b) c) v(r) ~ r v(r) ~ r 0,5 v(r) ~ r -0,5 Ażeby uzyskać rozkład gęstości w funkcji odległości od centrum Galaktyki, należy przyjąć założenie, że wewnątrz powłoki sferycznej nie ma pola grawitacyjnego. Jeżeli przyjmiemy, że rozkład materii w halo galaktycznym ma rozkład sferyczny [6], to siła dośrodkowa działająca na masę m jest równa sile grawitacji pochodzącej od kuli o promieniu r.
, gdzie , stąd Różniczkując stronami ostatnie równanie i uwzględniając (3) uzyskujemy odpowiednio następujące rozkłady gęstości:
(4)
a) b) c) 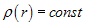
C - stała
po uwzględnieniu wzorów (4):
(4)
a) b) c) 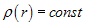
z dokładnością do stałej (potencjał niecechowany) otrzymujemy:
(5)
a) b) c) 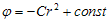
Przykłady prostych potencjałów na zewnątrz jednorodnej kuli (2a) i sfery możemy spotkać w [8]. Są one takie same jak dla masy punktowej i nie będziemy się w tej pracy nimi zajmować. Wyznaczanie potencjałów o bardziej skomplikowanej strukturze matematycznej (np. wzory (5)) wymaga już znajomości rachunku całkowego i leży poza możliwościami ucznia szkoły średniej.
Wykresy potencjałów - program komputerowy
Poniższy program pozwala w sposób numeryczny obliczać potencjały i jednocześnie uzyskać ich trójwymiarową reprezentację graficzną. Program jest napisany w darmowo dostępnym języku FreeBasic. Język ten został wybrany ze względu na prostotę operacji graficznych oraz osobiste preferencje autora.
' STUDNIA POTENCJAŁU GRAWITACYJNEGO
'----------------------------------
'(C)2007 mgr Tadeusz Sypek
OPTION EXPLICIT
PUBLIC FUNCTION f(BYVAL r AS DOUBLE) AS DOUBLE
RETURN -r * r + 33
END FUNCTION
CLS: SCREEN 9: WINDOW (-320, 175)-(319, -174)
' USTALANIE DOLNEGO HORYZONTU
DIM min(629) AS DOUBLE
DIM AS INTEGER a, b
DIM AS DOUBLE r, pot, x, y, dr
FOR a = 1 TO 629
min(a) = -50 * SIN((a - 1) / 100)
NEXT
dr = 0.01
FOR r = 1 TO .01 STEP -dr
pot -= f(r) * r * dr
FOR a = 1 TO 629 STEP 20
x = -150 * r * COS((a - 1) / 100)
y = -50 * r * SIN((a - 1) / 100) + 10 * pot
' PRZESŁANIANIE
IF a < 314 THEN PSET (x, y)
IF y >= -min(a) AND a > 314 THEN PSET (x, y)
IF 100 * r MOD 10 = 0 THEN
FOR b = 1 TO 629
x = -150 * r * COS((b - 1) / 100)
y = - 50 * r * SIN((b - 1)/ 100) + 10 * pot
IF b < 315 THEN PSET (x, y)
IF y >= -min(b) AND b > 315 THEN PSET (x, y)
NEXT
END IF
NEXT
NEXT
SLEEP
END
Komentarz do programu
RETURN -r * r + 33
END FUNCTIONFunkcja f wyznacza wartości funkcji gęstości, dla której pragniemy uzyskać przestrzenny wykres potencjału.
min(a) = -50 * SIN((a - 1) / 100)
NEXTW celu przyspieszenia obliczeń wypełniamy tablicę min() wartościami funkcji sinus z przedziału 0 do 2π, wymnożonymi przez -50.
FOR r = 1 TO .01 STEP -dr
pot -= f(r) * r * dr
FOR a = 1 TO 629 STEP 20
x = -150 * r * COS((a - 1) / 100)
y = -50 * r * SIN((a - 1) / 100) + 10 * potw pierwszej pętli obliczamy wartości dla dolnego horyzontu, który jest wykorzystywany do tworzenia linii przesłaniania,
w drugiej pętli liczone są wartości potencjału w funkcji odległości od środka ruchu,
IF y >= -min(a) AND a > 314 THEN PSET (x, y)
IF 100 * r MOD 10 = 0 THEN
FOR b = 1 TO 629
x = -150 * r * COS((b - 1) / 100)
y = - 50 * r * SIN((b - 1)/ 100) + 10 * pot
IF b < 315 THEN PSET (x, y)
IF y >= -min(b) AND b > 315 THEN PSET (x, y)
NEXT
END IF
NEXT
NEXTinstrukcje warunkowe pozwalające kreślić linie równoleżnikowe i południkowe (głębne).
Zwróćmy uwagę, że linie równoleżnikowe są liniami ekwipotencjalnymi.
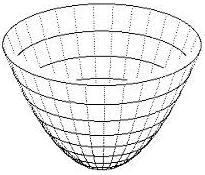
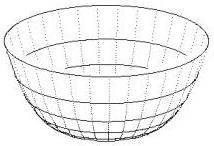
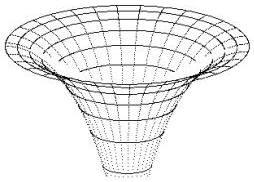
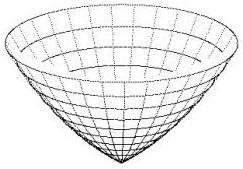
Ryc.3 a, b, c przedstawiają wyniki działania programu dla rozkładów gęstości określonych wzorami (4a, b, c).
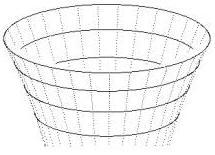
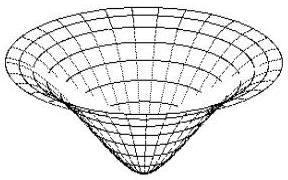
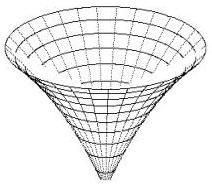
Wykresy przestrzenne potencjałów mają kształt charakterystycznych tworów, które nazywamy jamami lub studniami potencjału. Dokładniej: jama (studnia) potencjału to ograniczony obszar przestrzeni, w którym energia potencjalna punktu materialnego (cząstki) przyjmuje wartość mniejszą (w mechanice klasycznej i kwantowej) niż w otoczeniu tego obszaru. Podstawową własnością jamy potencjału jest zdolność do zatrzymywania w niej cząstki o energii mniejszej od energii potencjalnej brzegu jamy. W takim stanie, cząstka porusza się tylko wewnątrz jamy potencjału, czyli pozostaje w ograniczonym obszarze przestrzeni. W mechanice klasycznej jama potencjału ma zawsze skończone rozmiary i cząstka w ogóle nie może przeniknąć poza granice tego obszaru.
Wielkości charakteryzujące jamę (studnię) potencjału:
- głębokość jamy; cechuje intensywność oddziaływania,
- szerokość; określa zasięg oddziaływania [9].Użytkownik również sam może zaproponować inne rozkłady gęstości przestrzennej materii wewnątrz kuli, które go interesują. Może to być także swoistą formą zabawy fizyczno-intelektualnej. Rys. 4a-d przedstawiają - zdaniem autora - takie ciekawe przypadki:
Już pobieżna analiza ryc. 3 i 4 pokazuje, że niektóre studnie potencjału nie mają dna. Matematycy kwitują to krótko: wartość r = 0 nie należy do dziedziny funkcji V(r), albo: funkcja V(r) nie jest określona dla r = 0. Fizyk natomiast mówi o osobliwości w tym punkcie i opisuje lub stara się opisać naturę fizyczną tego fragmentu przestrzeni, o ile oczywiście pozwala na to aktualny stan wiedzy.

Ponieważ zaczęliśmy nasze rozważania od galaktyk, postawmy pytanie jak w tytule rozdziału.
Jeszcze przed powstaniem astronomii gwiazdowej, zwanej wówczas (koniec XVIII w. - pocz. XIX.), "astronomią odległych gwiazd", wygłaszane były poglądy o obecności w centrum naszej Galaktyki masywnych gwiazd. Angielski uczony Tomas Wright w 1750 r. twierdził na przykład, że widzialny pas Drogi Mlecznej oraz otaczające go gwiazdy tworzą system o kształcie młyńskiego koła lub płaskiego dysku. Według Immanuela Kanta (1755 r.) w środku Galaktyki musi istnieć ciało o wyjątkowej dużej masie; uważał, że mógłby być nim Syriusz(!) Z kolei, Johann Heirich Lambert (1761 r.), formułując pogląd o strukturalnej nieskończoności Wszechświata sądził, że Droga Mleczna jest tworem wyższego rzędu, skupionym wokół gigantycznego ciała centralnego [10].
W następnych dziesięcioleciach, badania nad ruchami własnymi gwiazd i ich paralaksami prowadzą do odkrycia, że centrum naszej Galaktyki znajduje się w gwiazdozbiorze Strzelca. Oczywiście, przystąpiono natychmiast do obserwacji tego fragmentu nieba, ale niczego ciekawego tam nie znaleziono. Dzisiaj wiemy, dlaczego; pył międzygwiazdowy utrudnia obserwacje w części widzialnej widma (absorpcja promieniowania wynosi 99%) [11].
Mimo tych ograniczeń astronomia gwiazdowa rozwija się szybko, wykorzystując osiągnięcia powstających nowych dziedzin fizyki i astronomii. Zastosowanie metod statystyki matematycznej, mechaniki statystycznej, astrofizyki i astrometrii oraz kinematyki i dynamiki układów gwiazdowych doprowadziło w latach dwudziestych do odkrycia ruchu obrotowego Galaktyki. Olbrzymie triumfy na polu obserwacyjnym (Oort, Zwicky) i teoretycznym (Kepteyn, Seeliger) odnosiła astronomia gwiazdowa w latach 20-30 - tych XX w., ale prawdziwy skok jakościowy nastąpił w latach 50-60-tych, w związku z rozwojem nowych technik obserwacyjnych (próbniki balonowe i radio-astronomia, obserwacje w podczerwieni, sztuczne satelity - astronomia pozaatmosferyczna), które pozwoliły na zbieranie danych z całego zakresu widma fal elektromagnetycznych.

Bardzo wcześnie, jeszcze w latach sześćdziesiątych, zaczęto podejrzewać, że w procesie emisji energii z Centrum Galaktyki muszą mieć swój udział obiekty o masach miliardy razy większych niż masa Słońca. Rozważano różne możliwości, wśród nich i taką, że w centrum galaktyki znajduje się ogromna gromada gwiazd, w której pojedyncze gwiazdy, jedna po drugiej, wybuchają jako supernowe. Jednak w 1963 r. F. Hoyle i W. A. Fowler wysuwają pogląd, że źródłem energii z Centrum może być grawitacyjne kurczenie się bardzo masywnego ciała. Logiczną konsekwencją tej hipotezy jest koncepcja masywnej czarnej dziury w Centrum, a wraz nią tzw. model standardowy.
Założenia wspomnianego modelu są następujące: w sąsiedztwie czarnej dziury znajduje się materia (pył i gaz), która posiada moment pędu związany z ruchem dookoła środka galaktyki. Gaz spadając po spirali w kierunku czarnej dziury wyzwala energię potencjalną grawitacji, która następnie, poprzez procesy termiczne może zostać wypromieniowana. Gaz opada na czarną dziurę nie wprost, ale tworzy rozgrzany wir, zwany dyskiem akrecyjnym (łac. acretio - wzrost, przybywanie). Dysk rotuje różnicowo, tzn., że różne jego warstwy mają różną prędkość, co prowadzi do nagłego wzrostu temperatury gazu. Olbrzymia wydajność procesu akrecji, powoduje, że dysk rozgrzewa się do kilku milionów stopni, a gorąca korona wokół dysku - do kilku miliardów stopni (!). W rezultacie obserwujemy radiowe i wysokoenergetyczne promieniowanie termiczne opisane prawem Plancka.
Ostatnie lata to następny, znaczący krok w rozwoju w narzędzi obserwacyjnych: (teleskopy Keck - 10m, teleskop kosmiczny Hable’a, astronomia rentgenowska i gamma); najnowsze doniesienia, na podstawie bardzo starannych obserwacji w Centrum, oceniono masę czarnej dziury na 2,6.106 mas Słońca [10]. Jeżeli przyjmiemy, że promień czarnej dziury odpowiadającej masie Słońca wynosi 3 km, to szacuje się, że rozmiary Centrum wynoszą:
(au = astronomical unit - jednostka astronomiczna - odległość Ziemia-Słońce). Mówimy oczywiście o tzw. promieniu grawitacyjnym, zwanym też promieniem Swarzchilda.
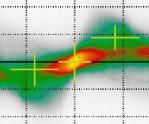
Czarna dziura w Centrum Galaktyki jest identyfikowana z radioźródłem Sgr A* (Sagittarius – Strzelec), które wysyła ogromne ilości energii, ok. 10 % emisji całej Galaktyki. Emisja tego radioźródła pochodzi od promieniowania synchrotronowego relatywistycznych elektronów, poruszających się w silnych polach magnetycznych. Dowody potwierdzające te hipotezę nie są jednak wystarczająco silne. Zwraca się uwagę na małe rozmiary Sgr A* (mniejsze niż promień orbity Marsa) i kształt widma, typowy dla promieniowania gazu spadającego na czarną dziurę. Dodatkowym argumentem jest niewielka prędkość Sgr A*. Obiekt o masie typowej dla gwiazdy w silnym polu grawitacyjnym, jakie mamy w środku Galaktyki, powinien poruszać się ze znaczną prędkością. Przeciwnicy twierdzą, że czarna dziura, która zbiera materię z otoczenia, musi być silnym źródłem promieniowania X (takie źródło rzeczywiście wykryto, ale jest ono dość słabe). Pozostawała jednak inna, choć mniej prawdopodobna, możliwość: pole grawitacyjne jest wytwarzane przez bardzo gęstą gromadę słabo świecących obiektów (np. gwiazd neutronowych) [12].
Jednym ze sposobów rozwiązania tych kontrowersji jest badanie ruchów gwiazd w Centrum Drogi Mlecznej. Można w ten sposób określić kształt i natężenie pola grawitacyjnego. Jak wiemy z lekcji fizyki natężenie pola jest ścisłe związane z potencjałem. Wracamy zatem jeszcze raz do postawionego w tytule artykułu pytania:
CO ZNAJDUJE SIĘ W CENTRUM GALAKTYKI?
Musimy jednak pamiętać, że badanie opisanego wyżej modelu, jego różnych rozwinięć i modyfikacji, a następnie ich weryfikacja jest dopiero pierwszym przybliżeniem opisu skomplikowanych zjawisk zachodzących w Centrum. Mimo rozpowszechnienia wspomnianego modelu nie brak wśród astrofizyków zwolenników innych rozwiązań. Jeszcze pod koniec lat 90-tych, pojawiały się doniesienia o gromadach białych karłów i pulsarów w Centrum, populacji pulsarów czy słabo świecących gwiazd neutronowych. W pobliżu centrum Galaktyki brak jakichkolwiek dramatycznych wydarzeń i dlatego do niedawna Drogę Mleczną zaliczano do tzw. galaktyk normalnych, to jest takich, że wokół centrum nie tworzy się dysk akrecyjny wskutek wyczerpania ”paliwa”. Ostatnio jednak pojawiła się hipoteza, że nasza galaktyka należy jednak do galaktyk aktywnych, tzn. w Centrum znajduje się aktywne jądro, gdzie źródłem promieniowania są nie tylko gwiazdy; przypuszczenie to ma coraz więcej zwolenników [13].
Rozważania o potencjale dotyczyły obiektów o symetrii sferycznej. Do takich należą również zwarte, silnie skoncentrowane skupiska gwiazd zwane gromadami kulistymi. Ale gromady i galaktyki nie są ostatnim szczeblem kosmicznej struktury, lecz grupują się w gromady galaktyk i supergromady. Rozmiary galaktyk sięgają 300 tysięcy lat świetlnych, gromad - 30 mln lat świetlnych, supergromad - 300 mln. Gromady zawierają od kilku-dziesięciu do kilku tysięcy galaktyk, supergromady - to kilka lub kilkanaście bogatych gromad galaktyk. Droga Mleczna znajduje w zespole 30 galaktyk zwanych Grupą Lokalną, która wraz z najbliższą gromadą w gwiazdo-zbiorze Panny wchodzi skład Lokalnej Supergromady.
Zakończenie
Przedstawiony program może również posłużyć do znajdowania potencjałów elektrostatycznych, gdy znany jest przestrzenny rozkład ładunków; należy tylko pamiętać o dwóch rodzajach oddziaływań, a zatem o znaku potencjału. Po niewielkich zmianach (usuwamy całkowanie numeryczne) łatwo dostosujemy program do bez-pośredniego, wizualnego przedstawiania potencjałów, o ile oczywiście jest znany ich kształt matematyczny. W ten sposób można przybliżyć poglądowo np. potencjały oscylatora czy rotatora harmonicznego, potencjały Yukawy, Van der Waalsa, grawitacyjnego z poprawkami relatywistycznymi itd. Możemy także, w pracy z uczniem uzdolnionym, pokusić się o przedstawienie graficzne różnych potencjałów rozpatrywanych w mechanice kwantowej. Przykłady takich potencjałów można znaleźć w [14], [15].
Literatura
| [1] | Kittel C., Knight W., Ruderman M., Mechanika, PWN, W-wa 1969, |
| [2] | Kleine M., Matematyka a świat fizyczny, PWN, W-wa 1964, |
| [3] | http://pl.wikipedia.org/wiki/Droga Mleczna, |
| [4] | Druga seria I etapu, XL Olimpiada Astronomiczna 1996/97, Komitet Główny Olimpiady Astronomicznej, Planetarium i Obserwatorium Astronomiczne w Chorzowie, |
| [5] | Pierwsza seria I etapu, XXXIX Olimpiada Astronomiczna 1995/96, Komitet Główny Olimpiady Astronomicznej, Planetarium i Obserwatorium Astronomiczne w Chorzowie, |
| [6] | Reeves H., Najnowsze wiadomości z Kosmosu. W stronę pierwszej sekundy, Wyd. Cyklady, 1996, |
| [7] | Kiraga M., Ciemna materia we Wszechświecie, Urania 7-8/95, |
| [8] | Salach J., Sagnowska B., Kreiner J., Fizyka z astronomią dla klasy II liceum ogólnokształcącego, WSiP, W-wa 1995, |
| [9] | Encyklopedia fizyki, t. 2, PWN, 1993, |
| [10] | Horský Z., Plavec M., Człowiek poznaje Wszechświat, PWN, W-wa 1966, |
| [11] | Życki P., Aktywne jądra galaktyk, Postępy Astronomii, 4/1996, |
| [12] | Czerny M. w: http://www.wiw.pl/nowinki/astronomia, |
| [13] | Sołtan A., Galaktyki normalne, Urania - Postępy Astronomii, 5/98, p. także: R. M. Hazen, Dlaczego czarne dziury nie są czarne; Prószyński i S-ka, 2002; Kitty Ferguson, Czarne dziury, czyli uwięzione światło, Prószyński i S-ka, 2002; Paul Devies, Czas. Niedokończona ewolucja Wszechświata, Prószyński i S-ka, 2002, |
| [14] | Średniawa B., Mechanika kwantowa, PWN, W-wa 1978, |
| [15] | Greczko L. K. i in., Sbornik zadacz po teorieticzieskoj fizikie, Wyższa Szkoła, Moskwa 1984. |
Dokument ten rozpowszechniany jest zgodnie z zasadami licencji GNU Free Documentation License. Źródło: http://www.i-lo.tarnow.pl/edu/ast/sim/sg/index.html
Autor: mgr Tadeusz Sypek