Gaz doskonały

POJĘCIE GAZU DOSKONAŁEGO

W fizyce bardzo często mamy do czynienia z modelami - idealizacjami pewnych zjawisk. Dzięki nim możemy chociaż w przybliżeniu opisywać pewne procesy, które zachodzą w rzeczywistości. W tym rozdziale będziemy częto posługiwać się modelem gazu doskonałego:

Gaz doskonały - definicja
Jedynym rodzajem oddziaływań cząsteczek w gazie doskonałym są zderzenia sprężyste pomiędzy cząsteczkami oraz ze ściankami naczynia.
Objętość cząsteczek gazu doskonałego jest zaniedbywalnie mała w porównaniu z objętością naczynia.

Gazy rzeczywiste zachowują się jak gaz doskonały tylko w odpowiednich warunkach: w wysokiej temperaturze (energia kinetyczna cząsteczek jest na tyle duża, że można zaniedbać energię oddziaływań elektromagnetycznych) i niskim ciśnieniu (gaz jest rozrzedzony, a dzięki temu rozmiary cząsteczek są małe w porównaniu do odległości między nimi).

Model ten ma zastosowanie do wszystkich gazów rzeczywistych, ale istnieją granice jego zastosowania, z którymi wiąże się kolejne pojęcie:

Temperatura zera bezwzględnego - definicja
Jest to najniższa temperatura, do której możemy się zbliżać, ale jej osiągnięcie jest niemożliwe (ciśnienie i objętość musiałyby być równe zeru). W temperaturze tej zanika całkowicie ruch cząsteczek. Temperatura ta jest równa -273,15 oC lub 0 K (kelwinów).

Skala Kelvina nazywana jest również bezwzględną skalą temperatur. Jednostkowy przyrost temperatury w obydwu skalach jest taki sam:

Δt = 1oC = 1K
T = t(oC) + 273,15 T - temp. w kelwinach

RÓWNANIE STANU GAZU DOSKONAŁEGO - RÓWNANIE CLAPEYRONA

Równanie Clapeyrona pokazuje zależność pomiędzy trzema jego właściwościami, które pozwalaja opisać go oraz wpływają na jego zachowanie: ciśnieniem, temperaturą i objętością.
Z teorii kinetyczno-molekularnej wiemy, że:

p = (2N)/(3V) .Eśr W fizyce jest wiele różnorakich stałych, niektóre z nich nie mają nawet nazwy. Podczas wyprowadzania równania Clapeyrona pojawi się ich kilka. Jedną z nich jest stała oznaczana symbolem C. Wyraża ona stosunek energii średniej cząsteczek gazu do jego temperatury: C=Eśr / T Zatem:p = (2N)/(3V) .Eśr i Eśr = T . C =>p = (2NTC)/(3V) Wprowadzamy kolejną stałą - k - zwaną stałą Boltzmana: k = 2/3 . C I po podstawieniu otrzymujemy:p = (kNT) / V Po obustronnym pomnożeniu przez V i podzieleniu przez T otrzymujemy: (pV)/T = kN Widać już, że iloraz iloczyny ciśnienia i objętości przez temperaturę (pV)/T jest zawsze stały, ponieważ k jest stałą, a i N=const (liczba cząsteczek nie ulega zmianie).
Rozpatrzmy teraz 1 mol gazu (mol to nie taki denerwujący owad, ale jednostka liczności materii, to powinno być na chemii :) Dla 1 mola gazu N = NA (NA - stałą Avogadro) - w jednym molu substancji jest zawsze tyle samo cząsteczek - 6,022 . 1023 - i to jest właśnie NA. Zatem można zapisać: (pV)/T = kNA Pojawia się już ostatnia stała w tym wyprowadzeniu, ale stała bardzo ważna - R - stała gazowa (R = 8,31 J / (mol . K)) : R = kNA Zatem po podstawieniu: (pV)/T = RDla n moli gazu: (pV)/T = nR

Po przekształceniu otrzymujemy równanie Clapeyrona:

pV = nRT  n = m/M jak wiadomo z chemii :) gdzie m to masa substacji, a M to masa molowe tej substancji. Zatem można zapisać jeszcze jedną postać tego równania: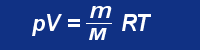

PRZEMIANY GAZOWE

Dla wszystkich przemian prawdziwa jest zależność:

(p1V1)/T1 = (p1V2)/T2 czyli, innymi słowy stosunek iloczyny ciśnienia i objętości do temperatury gazu jest zawsze taki sam.

Przemiana izotermiczna jest nazywana również prawem Boyle'a - Mariotte'a. Jak sama nazwa wskazuje, w przemianie tej temperatura nie ulega zmianie:

T = const w związku z tym również: pV = const  

   Wykres ten przedstawia zależność ciśnienia od   objętośći dla gazu w przemianie izotermicznej. Krzywa   ta nazywa się izotermą.

 

Przemiana izohoryczna stałej masy gazu charakteryzuje się niezmiennością objętości. Przyrost ciśnienia jest wprost proporcjonalny do przyrostu temperatury.

V = const

p / T = const

 

 

 

Równanie tej prostej, zwanej również izochorą można zapisać :

p = (Δp / Δt) . t + p0

Przemiana izobaryczna zachodzi, gdy ciśnienie stałej masy gazu nie ulega zmianie. Przyrots objętości jest wprost proporcjonalny do przyrostu temperatury.

p = const

V / T = const

  Równaniej tej prostej zwanej izobarą można zapisać:

V = (ΔV / Δt) . t + V0

 

Źródło: http://www.superfizyka.za.pl/