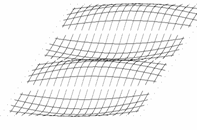
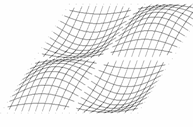
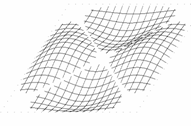
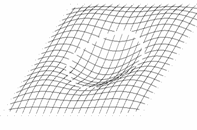
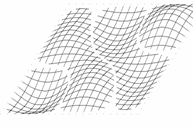
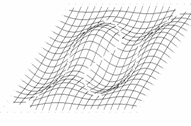
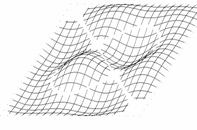
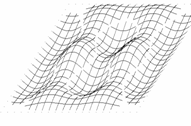
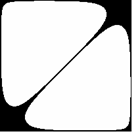
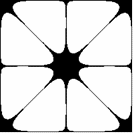
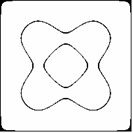
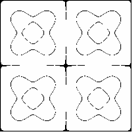
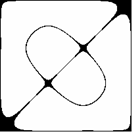
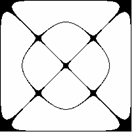
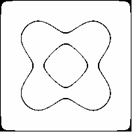
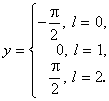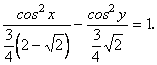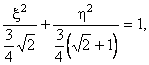Przyjmijmy, że poruszamy się w obszarze zmienności funkcji (1.1), określonym przez rozmiary płyty:
(x,y)
D2, D = <0,p>.
Wygodniej będzie badać linie funkcyjne, gdy układ współrzędnych przeniesiemy do środka figury
(translacja o wektor). W pierwszej chwili formalny zapis komplikuje się:
| a) | b) | c) |
| d) | e) | f) |
| g) | h) | i) |
ale jak się okaże niżej, w ogólnym rozrachunku będzie to opłacalne. Obszar zmienności funkcji (1.2) wówczas:
(x,y)
D12, D1 =
a) okresowość funkcji i wielokrotność argumentu
a)
1 : 2; -p/4b)
2 : 4; -p/4c)
1 : 5; p/4d)
2 : 10; p/4Mówiąc o okresie funkcji (1.2) musimy osobno rozróżniać okres względem zmiennej x i zmiennej y. Z uwagi na podobieństwo wyrażeń występujących w rozpatrywanej funkcji wystarczy udowodnić, że
jest funkcją okresową, czyli że:
T - okres funkcji.
Po przeniesieniu wyrazów na jedną stronę i zastosowaniu wzoru na sinus różnicy kątów:
Ponieważ pierwszy czynnik nie jest tożsamościowo równy zeru:
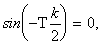
k
C \ {0}, T = 2p jest okresem podstawowym (zasadniczym).
Z pojęciem okresu wiąże się również problem wielokrotności argumentu funkcji.
Rozpatrzmy prosty przypadek a = 0.
k
<0, m>, k Î C, l <0,n>, l Î C.
np. dla m = 3, n = 2 (Rys. 4b) otrzymujemy siatkę prostych:
Ç
a)
2 : 2; 0b)
3 : 2; 0b) analiza matematyczna niektórych figur płaskich
Stosunek częstotliwości drgań własnych 3 : 1 (a = p/4 i a = -p/4):
Wprowadzamy fazę: a = p/4 i a= -p/4. Po drobnych przekształceniach otrzymujemy:
dla a = p/4:
dla a = -p/4:
Stosując wzór na funkcje wielokrotności kąta: sin3j = 3sinj - 4sin3j, a następnie wzory redukcyjne i odpowiednio grupując wyrazy:
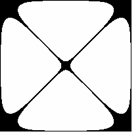
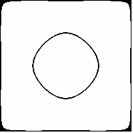
Wprowadźmy nowe zmienne: cosx = x i cosy = h. Pierwsze równanie (2.2) można by nazwać równaniem quasiokręgu x2 + h2 = 2/3 (Rys. 5a), a drugie jest po prostu równaniem pary prostych x = h Ç x = -h (Rys. 5b). Oprócz równań otrzymujemy równania brzegów figury (xh = 0), które w tym przykładzie i następnych pomijamy.
Rys. 5
a)
3 : 1; -p/4b)
3 : 1; p/4Stosunek częstotliwości drgań własnych 3 : 1 (a = p/8 i a = -p/8)
Zauważmy od razu, że:
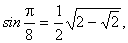
Stosując wzór na funkcję wielokrotności kąta: sin3j = 3sinj - 4 sin3j a następnie wzory redukcyjne otrzymujemy:
dla :
dla :
Opuszczając nawiasy i grupując wyrazy
i odpowiednio:
Po przekształceniach:
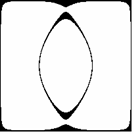
Wprowadźmy w podobny sposób, jak wyżej, nowe zmienne: cos2x = x i cos2y = h Powyższe równania można by nazwać odpowiednio równaniem elipsy (Rys. 6a) i quasi-hiperboli (Rys. 6b):
Rys. 6
a)
3 : 1; p/8b)
3 : 1; -p/8Stosunek częstotliwości drgań własnych 4 : 1 ( a = p/4 i a = -p/4 )
dla a = p/4:
dla a = -p/4:
Skorzystajmy dwukrotnie ze wzoru na sinus kąta podwojonego:
Posługując się nim, a następnie grupując wyrazy (wzory na sumę i różnicę sześcianów) otrzymujemy:
i odpowiednio
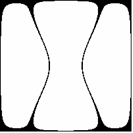
Jeżeli oznaczymy sinx = x oraz siny = h, to dla a = p/4 oprócz prostej x = -h otrzymujemy równanie quasielipsy x2 + 3h2 = 1 obróconej o kąt a = p/4 (x2 - xh + h2 = 1/2) (Rys. 7a), a dla a = -p/4 prostą x = h oraz równanie tej samej quasielipsy w obrocie o kąt a = -p/4 (x2 xh + h2 = 1/2) (Rys. 7b).
a)
4 : 1; p/4b)
4 : 1; -p/4Stosunek częstotliwości drgań własnych 5 : 1 (a = p/4 i a = -p/4)
Posłużmy się tożsamością: Poprawności jej dowodzimy korzystając np. ze wzoru na sinus sumy kątów
, albo posługując się gotowym wzorem na sinka, który wyprowadza się na gruncie liczb zespolonych, przy pomocy dwumianu Newtona i formuły Moivre'a [4].
+Po wprowadzeniu fazy a i zastosowaniu wzorów redukcyjnych
dla a = p/4, 5cos2x - 4cos4x - 5cos2y + 4cos4y = 0,
dla a = -p/4, 5 - 20cos2x + 16cos4x + 5 - 20cos2y + 16cos4y = 0.
Stosując wzory skróconego mnożenia oraz grupując wyrazy otrzymujemy następujące rozwiązania:
i odpowiednio:
Jeżeli w równaniu (2.4) wprowadzimy oznaczenia: cosx = x, cosy = h, a w (2.5) ![]()
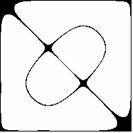
![]() to wówczas równanie (2.4) przedstawia parę prostych x = h Ç x = -h i quasiokrąg x2 + h2 = 5/4 (Rys. 8a), natomiast równanie (2.5) przedstawia wtedy równanie quasiokręgu rzędu 2-go (Rys. 8b).
to wówczas równanie (2.4) przedstawia parę prostych x = h Ç x = -h i quasiokrąg x2 + h2 = 5/4 (Rys. 8a), natomiast równanie (2.5) przedstawia wtedy równanie quasiokręgu rzędu 2-go (Rys. 8b).
| a) | b) |
GNU Free Documentation License.
Źródło: mgr Tadeusz Sypek