
Z definicji liczb pierwszych wynika, iż wszystkie liczby naturalne większe od jeden dzielą się na dwa rodzaje:
- liczby pierwsze, które mają tylko jeden dzielnik pierwszy - same siebie
- liczby złożone, które są iloczynem dzielników pierwszych.
Rozkład liczby na czynniki pierwsze polega na znalezieniu wszystkich jej dzielników pierwszych. Na przykład liczba 40 rozkłada się na następujące czynniki pierwsze:
40 = 2  2
2  2
2  5
5
Czynniki pierwsze mogą występować wielokrotnie. W rozdziale o generacji liczb pierwszych podaliśmy rozkład czynników pierwszych dowolnej liczby naturalnej. Wynika z niego, iż czynniki pierwsze koncentrują się w przedziale od 2 do pierwiastka z n. Poza tym przedziałem może być co najwyżej jeden czynnik pierwszy.

| Rozkład liczby 330 na czynniki pierwsze |
| n | p | Opis | g | Czynniki | Uwagi |
| 330 | : 2 | = 165 | [√330] = 18 | 2 | p = liczba pierwsza |
| 165 | : 2 | - nie dzieli się, p := p + 1, p < g | 2 | |
| 165 | : 3 | = 55 | 2 3 | p = liczba pierwsza |
| 55 | : 3 | - nie dzieli się, p := p + 1, p < g | 2 3 | |
| 55 | : 4 | - nie dzieli się, p := p + 1, p < g | 2 3 | 4 = 2  2, a te czynniki już były 2, a te czynniki już były |
| 55 | : 5 | = 11 | 2 3 5 | p = liczba pierwsza |
| 11 | : 5 | - nie dzieli się, p := p + 1, p < g | 2 3 5 | |
| 11 | : 6 | - nie dzieli się, p := p + 1, p < g | 2 3 5 | 6 = 2  3, czynniki już były 3, czynniki już były |
| 11 | : 7 | - nie dzieli się, p := p + 1, p < g | 2 3 5 | p = liczba pierwsza |
| 11 | : 8 | - nie dzieli się, p := p + 1, p < g | 2 3 5 | 8 = 2  2 2  2, czynniki już były 2, czynniki już były |
| 11 | : 9 | - nie dzieli się, p := p + 1, p < g | 2 3 5 | 9 = 3  3, czynniki już były 3, czynniki już były |
| 11 | : 10 | - nie dzieli się, p := p + 1, p < g | 2 3 5 | 10 = 2  5, czynniki już były 5, czynniki już były |
| 11 | : 11 | = 1 | 2 3 5 11 | p = liczba pierwsza |
| 1 | | n = 1, kończymy | 2 3 5 11 | |
Zwróć uwagę, iż pomimo tego, że p przebiega kolejne liczby naturalne, n dzieli się bez reszty przez p tylko wtedy, gdy p jest liczbą pierwszą. Działa tutaj podobny mechanizm do sita Eratostenesa - liczbę n dzielimy dotąd przez p, aż przestanie to być możliwe. Jest to równoważne wyrzucaniu wszystkich wielokrotności danego podzielnika z n. W wyniku n przestaje być podzielne przez wszystkie dotychczasowe p. Zatem nie jest również podzielne przez liczby złożone z poprzednio wyznaczonych podzielników.

jeśli wyznaczyliśmy wszystkie czynniki 2 i 3, to wynikowa liczba n nie dzieli się już przez 4 (2  2), 6 (2
2), 6 (2  3), 9 (3
3), 9 (3  3) itd. jedynymi możliwymi podzielnikami są dalsze liczby pierwsze nie zawierające już wyznaczonych czynników.
3) itd. jedynymi możliwymi podzielnikami są dalsze liczby pierwsze nie zawierające już wyznaczonych czynników.

Dane wejściowe
| n | - liczba rozkładana na czynniki pierwsze, n  N N |
Dane wyjściowe
Ciąg liczb pierwszych, których iloczyn daje liczbę n.
Zmienne pomocnicze
| g | - górna granica dzielników pierwszych, g  N N |
| p | - dzielnik, p  N N |

| krok 1: | Czytaj n |
| krok 2: | p 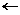 2; g 2; g 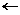 pierwiastek całkowity z n pierwiastek całkowity z n |
| krok 3: | Dopóki p 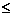 g, wykonuj kroki 4...7. Inaczej idź do kroku 8. g, wykonuj kroki 4...7. Inaczej idź do kroku 8. |
| krok 4: | Dopóki (n mod p) = 0, wykonuj kroki 5,6. Inaczej idź do kroku 7. |
| krok 5: | n 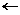 [n : p] [n : p] |
| krok 6: | Pisz p |
| krok 7: | Jeśli n > 1, to zwiększ p 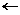 p + 1 i kontynuuj pętlę od kroku 3. Inaczej zakończ algorytm. p + 1 i kontynuuj pętlę od kroku 3. Inaczej zakończ algorytm. |
| krok 8: | Jeśli n > 1, to pisz n |
| krok 9: | Zakończ algorytm |

Odczytujemy liczbę n.
Jako pierwszy podzielnik p przyjmujemy liczbę 2. Granicą podzielników będzie pierwiastek całkowity z liczby n. Wartość tę zapamiętujemy w zmiennej g.
Pętla nr 1 wykonuje się do wyczerpania podzielników p.
Pętla nr 2 wykonuje się dotąd, aż podzielnik p przestaje dzielić bez reszty liczbę n.
Po wyjściu z pętli nr 2 sprawdzamy, czy n = 1. Jeśli tak, to zostały znalezione już wszystkie dzielniki liczby n. Przerywamy zatem pętlę nr 1 i kończymy algorytm.
W przeciwnym razie zwiększamy p o 1, czyli bierzemy następny podzielnik i kontynuujemy pętlę nr 1
Po zakończeniu pętli nr 1 zostały znalezione wszystkie podzielniki z przedziału od 2 do całkowitego pierwiastka z n. Jeśli końcowe n > 1, to ma ono wartość ostatniego podzielnika leżącego poza tym przedziałem. W takim przypadku wypisujemy go i kończymy algorytm.

| Wydruk z uruchomionego programu |
Rozkład liczby n na czynniki pierwsze
--------------------------------------
(C)2005 mgr Jerzy Wałaszek I LO Tarnów
Podaj n = 25347
Czynniki pierwsze liczby 25347 to:
3 7 17 71
Koniec, naciśnij klawisz ENTER... |
| Microsoft Visual Basic 2005 Express Edition |
Borland
Delphi 7.0
Personal
Edition | // Rozkład liczby naturalnej na czynniki pierwsze
// (C)2004 mgr Jerzy Wałaszek I LO w Tarnowie
//-----------------------------------------------
program czprw;
{$APPTYPE CONSOLE}
var
n,p,g : cardinal;
begin
writeln('Rozklad liczby n na czynniki pierwsze');
writeln('--------------------------------------');
writeln('(C)2004 mgr Jerzy Walaszek I LO Tarnow');
writeln;
write('Podaj n = '); readln(n);
writeln;
if n < 2 then
writeln('Zle dane! Liczba n musi byc wieksza od 1')
else
begin
writeln('Czynniki pierwsze liczby ',n,' to:');
writeln;
p := 2;
g := round(sqrt(n));
while p <= g do
begin
while (n mod p) = 0 do
begin
n := n div p;
write(p,' ');
end;
if n = 1 then break;
p := p + 1;
end;
if n > 1 then write(n);
writeln;
end;
writeln; writeln('Nacisnij Enter...'); readln;
end. |
Borland
C++ Builder
6.0
Personal
Edition | // Rozkład liczby naturalnej na czynniki pierwsze
// (C)2004 mgr Jerzy Wałaszek I LO w Tarnowie
//-----------------------------------------------
#include <cmath>
#include <iostream>
using namespace std;
main()
{
unsigned n,p,g;
char s[1];
cout << "Rozklad liczby n na czynniki pierwsze\n"
"--------------------------------------\n"
"(C)2004 mgr Jerzy Walaszek I LO Tarnow\n\n"
"Podaj n = ";
cin >> n;
cout << endl;
if(n < 2)
cout << "Zle dane! Liczba n musi byc wieksza od 1\n";
else
{
cout << "Czynniki pierwsze liczby " << n << " to:\n\n";
p = 2; g = (unsigned)sqrt((double)n);
while(p <= g)
{
while(!(n % p))
{
n /= p; cout << p << ' ';
}
if(n == 1) break;
p++;
}
if(n > 1) cout << n;
}
cout << "\n\nKlawisz Enter = KONIEC";
cin.getline(s,1);
cin.getline(s,1);
} |
Microsoft
Visual
Basic 2005
Express
Edition | ' Rozkład liczby naturalnej na czynniki pierwsze
' (C)2005 mgr Jerzy Wałaszek I LO w Tarnowie
'-----------------------------------------------
Option Explicit On
Module Module1
Sub main()
Dim n, p, g As UInteger
Console.WriteLine("Rozkład liczby n na czynniki pierwsze")
Console.WriteLine("--------------------------------------")
Console.WriteLine("(C)2005 mgr Jerzy Wałaszek I LO Tarnów")
Console.WriteLine()
Console.Write("Podaj n = ")
n = Val(Console.ReadLine)
Console.WriteLine()
If n < 2 Then
Console.WriteLine("Złe dane! Liczba n musi być większa od 1")
Else
Console.WriteLine("Czynniki pierwsze liczby {0} to:", n)
Console.WriteLine()
p = 2 : g = Int(Math.Sqrt(n))
While p <= g
While (n Mod p) = 0
n = n \ p : Console.Write("{0} ", p)
End While
If n = 1 Then Exit While
p += 1
End While
If n > 1 Then Console.Write(n)
Console.WriteLine()
End If
Console.WriteLine()
Console.WriteLine("Koniec, naciśnij klawisz ENTER...")
Console.ReadLine()
End Sub
End Module |
| Python | # -*- coding: cp1250 -*-
# Rozkład liczby naturalnej na czynniki pierwsze
# (C)2005 mgr Jerzy Wałaszek I LO w Tarnowie
#-----------------------------------------------
import math
print "Rozklad liczby n na czynniki pierwsze"
print "--------------------------------------"
print "(C)2005 mgr Jerzy Walaszek I LO Tarnow"
print
n = int(raw_input("Podaj n = "))
print
if n < 2: print "Zle dane! Liczba n musi byc wieksza od 1"
else:
print "Czynniki pierwsze liczby", n, "to:"
print
p, g = 2, int(math.sqrt(n))
while p <= g:
while not (n % p):
n //= p
print p,
if n == 1: break
p += 1
if n > 1: print n,
print
print
raw_input("Nacisnij Enter...") |
| JavaScript | <html>
<head>
</head>
<body>
<form name="frmrozkld"
style="border: 1px outset #FF9933;
padding-left: 4px;
padding-right: 4px;
padding-top: 1px;
padding-bottom: 1px;
background-color: #FFCC66">
<h3 style="text-align: center">
Rozkład liczby n na czynniki pierwsze
</h3>
<p style="text-align: center">
(C)2004 mgr Jerzy Wałaszek - I LO w Tarnowie
</p>
<hr>
<p style="text-align: center">
n = <input type="text" name="inp_n" size="20" value="1012">
</p>
<p style="text-align: center">
<input type="button" value="Czynniki" name="B1" onclick="main()">
</p>
<p id="data_out" style="text-align: center">...</p>
</form>
<script language=javascript>
// Rozkład liczby naturalnej na czynniki pierwsze
// (C)2004 mgr Jerzy Wałaszek I LO w Tarnowie
//-----------------------------------------------
function main()
{
var n,p,g,s;
n = parseInt(document.frmrozkld.inp_n.value);
if(isNaN(n) || (n < 2))
s = "<font color=Red><b>Złe dane!</b></font>";
else
{
s = ""; p = 2; g = Math.floor(Math.sqrt(n));
while(p <= g)
{
while(!(n % p))
{
n /= p; s += p + " ";
}
if(n == 1) break;
p++;
}
if(n > 1) s += n;
}
document.getElementById("data_out").innerHTML = s;
}
</script>
</body>
</html> |
Dokument ten rozpowszechniany jest zgodnie z zasadami licencji
GNU Free Documentation License.
Źródło: mgr Jerzy Wałaszek
2
2
5
![]()
2, a te czynniki już były
3, czynniki już były
2
2, czynniki już były
3, czynniki już były
5, czynniki już były
![]()
2), 6 (2
3), 9 (3
3) itd. jedynymi możliwymi podzielnikami są dalsze liczby pierwsze nie zawierające już wyznaczonych czynników.
N
N
N
2; g
pierwiastek całkowity z n
g, wykonuj kroki 4...7. Inaczej idź do kroku 8.
[n : p]
p + 1 i kontynuuj pętlę od kroku 3. Inaczej zakończ algorytm.
