Zastosowanie komputera do symulacji różnych procesów świata rzeczywistego wymaga konieczności stwarzania sytuacji losowych. Osiągamy to za pomocą specjalnej funkcji, która nosi nazwę Generatora Liczb Losowych (Random Number Generator - RNG). Przez liczby losowe będziemy rozumieć ciąg liczb, pomiędzy którymi nie zachodzi zależność funkcyjna, tzn. pojawienie się danej liczby w tym ciągu można przewidzieć tylko z pewnym prawdopodobieństwem. Rozkład liczb losowych będzie liniowo równomierny, jeśli każda z nich pojawia się z tym samym prawdopodobieństwem (możliwe są również nieliniowe rozkłady generowanych liczb, np. rozkład Gaussa).
"Czyste" liczby losowe są bardzo trudne do uzyskania w komputerze, który jest maszyną deterministyczną, co oznacza, iż każda wykonywana przezeń operacja jest ściśle określona (zdeterminowana). Wymagany jest dostęp do zewnętrznego źródła sygnałów losowych, np. szumu radiowego, szumu elektrycznego w układach cyfrowych, itp. Odczytany sygnał losowy przetwarza się na postać cyfrową i odpowiednio obrabia, aby otrzymać liczbę losową w zadanym zakresie wartości. Ponieważ sygnał zewnętrzny nie jest zależny od procesów obliczeniowych komputera, to otrzymamy liczbę losową, której jakość zależy od jakości sygnału użytego jako źródło (najlepszy jest tzw. biały szum - sygnał, który zawiera składowe o równomiernym rozkładzie w całym paśmie odbiorczym). Tak wygenerowanej liczby nie da się w żaden sposób konkretnie przewidzieć na podstawie liczb wygenerowanych wcześniej (podobnie jak nie da się przewidzieć numerów w losowaniu Multilotka).
Jednakże takie podejście nie zawsze jest możliwe do zastosowania w typowym komputerze osobistym z uwagi na brak odpowiednich urządzeń (były co prawda próby wykorzystania jako źródła sygnałów losowych wejścia mikrofonowego karty dźwiękowej, jednakże nie wszystkie komputery są wyposażane w mikrofony, a karty dźwiękowe posiadają bardzo duży rozrzut parametrów, więc projekt nie powiódł się), dlatego zadawalamy się tworzeniem liczb pseudolosowych (pseudo oznacza jakby). Liczby takie wyglądają jak losowe, posiadają ich własności rozkładu prawdopodobieństwa, lecz są tworzone algorytmicznie. Dlatego znając generator liczb pseudolosowych (Pseudorandom Number Generator - PRNG) można przewidzieć kolejną liczbę pseudolosową na podstawie liczb poprzednio wygenerowanych. Co więcej, liczby pseudolosowe tworzą ciąg wartości, który po pewnym okresie jest powtarzany.
Funkcje generujące liczby pseudolosowe korzystają z różnych wzorów, w zależności od których dokonujemy podziału generatorów liczb pseudolosowych. W naszym opracowaniu opiszemy, ze względu na powszechność, generatory liniowe (Linear Congruential Generators - LCG), które korzystają z następującego wzoru przy wyliczaniu kolejnych liczb pseudolosowych:
| Liniowy Generator Liczb Pseudolosowych | |
|---|---|
| Xi = (aXi-1 + c) mod m | X - liczba pseudolosowa a - mnożnik c - przyrost m - moduł |
| Xi = (aXi-1 + c) mod m | c |
| Xi = aXi-1 mod m | c = 0 - generator multiplikatywny |
Na podstawie wzoru generacyjnego można wysnuć wiele własności generatora liczb pseudolosowych. Dla przykładu rozważmy generator mieszany:
Xi = (aXi-1 + c) mod m
Kolejne liczby pseudolosowe są resztami z dzielenia wyrażenia (aXi-1 + c) przez moduł m. Jakie wartości mogą przyjmować reszty z dzielenia? Oczywiście od 0 (gdy wyrażenie jest podzielne przez moduł) do m-1 (reszta z dzielenia jest zawsze mniejsza od dzielnika).
Ile różnych liczb pseudolosowych może być wygenerowane? Tyle, ile mieści się w przedziale od 0 do m-1, czyli m liczb.
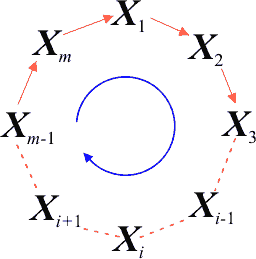
Ponieważ kolejne liczby pseudolosowe powstają z poprzednich, to ich następstwo w wygenerowanym ciągu nie jest dowolne, lecz wytyczone podanym wzorem. Liczby tworzą zamknięty pierścień, gdzie po Xm następuje ponownie X1.
Wzór pozwala wygenerować nową liczbę pseudolosową Xi na podstawie poprzednio wygenerowanej Xi-1. Problem pojawia się przy pierwszej liczbie X1, gdy nie istnieje jeszcze poprzednio wygenerowana liczba pseudolosowa. W takim przypadku za Xi-1 wstawiamy Xo, które nosi nazwę ziarna generatora pseudolosowego (ang. Random Seed). Wartość Xo jest równa dowolnej wartości z przedziału od 0 do m-1. Ze ziarna powstają pozostałe liczby pseudolosowe.
Na co wpływa ziarno Xo? Przyjrzyjmy się pierścieniowi. Następstwo kolejno generowanych liczb pseudolosowych jest zawsze takie samo i tego ziarno nie zmienia. Ziarno może jednak wybrać liczbę pseudolosową w pierścieniu, od której rozpocznie się generacja następnych liczb. Zatem określa ono punkt startowy pierścienia.
Podsumujmy:
- Mieszany generator liniowy liczb pseudolosowych tworzy liczby pseudolosowe w zakresie od 0 do m-1.
- Jeśli współczynniki generatora są dobrane prawidłowo, to generowane jest m różnych liczb pseudolosowych.
- Liczby pseudolosowe tworzą zamknięty pierścień wartości, w którym ustalona jest kolejność generowanych liczb.
- Liczby pseudolosowe powtarzają się w pierścieniu z okresem m.
- Pierwszą liczbę pseudolosową tworzymy na podstawie ziarna Xo.
- Ziarno wybiera punkt startowy pierścienia wartości liczb pseudolosowych.
- Ziarno nie wpływa na kolejność wartości liczb pseudolosowych w pierścieniu.
Dobór współczynników dla generatora liczb pseudolosowych Oto podstawowe reguły, które pozwalają zaprojektować dowolny mieszany generator liczb pseudolosowych:
1. Określamy przedział liczbowy, w obrębie którego mają być generowane liczby pseudolosowe:
n - maksymalna liczba pseudolosowa.
[0...n] - przedział dla generatora mieszanego
[1...n] - przedział dla generatora multiplikatywnego2. Moduł jest zawsze o 1 większy niż największa liczba pseudolosowa wygenerowana przez dany generator.
m = n + 1, gdzie n - maksymalna liczba pseudolosowa.3. Przyrost c i moduł m muszą być względnie pierwsze. Oznacza to, iż nie mogą posiadać wspólnych czynników pierwszych. Sam przyrost c nie musi być liczbą pierwszą. Krok ten pomijamy dla generatora multiplikatywnego. 4. Wartość wyrażenia (a - 1) musi być podzielna przez każdy czynnik pierwszy modułu m. Jeśli moduł m dzieli się przez 4, to (a - 1) również powinno dzielić się przez 4. Każdy liniowy generator liczb pseudolosowych można jednoznacznie zdefiniować za pomocą czwórki liczb:
LCG(m,a,c,Xo)
czyli modułu, mnożnika, przyrostu i ziarna.
![]()
Projekt generatora liczb pseudolosowych Określamy przedział wartości generowanych liczb pseudolosowych od 0 do 7.
n = 7.
Stąd m = n + 1 = 7 + 1 = 8Aby obliczyć przyrost c, najpierw rozbijamy moduł m na czynniki pierwsze:
m = 8 = 22
2
Przyrost c jest dowolną liczbą, która nie posiada czynnika 2. Przyjmujemy pierwszą liczbę o tej własności:
c = 3 (8 i 3 są liczbami względnie pierwszymi)Wyrażenie (a - 1) musi być podzielne przez 2 i 4 (wystarczy oczywiście podzielność przez 4), ponieważ 2 jest czynnikiem pierwszym modułu i dodatkowo moduł jest podzielny przez 4. Możemy zatem przyjąć:
(a - 1) = 4 czyli a = 4 + 1 = 5Posiadamy już komplet danych do utworzenia generatora liczb pseudolosowych: a = 5, c = 3 i m = 8. Zatem nasz generator wyraża się wzorem: Xi = (5Xi-1 + 3) mod 8
Jest to generator typu LCG(8,5,3,Xo), gdzie Xo przybiera wartości od 0 do 7.
Policzmy dla przykładu kilka liczb pseudolosowych za pomocą otrzymanego wzoru. Za Xo przyjmijmy liczbę 0:
X1 = (5
Xo + 3) mod 8 = (5
0 + 3) mod 8 = 3 mod 8 = 3
X2 = (5X1 + 3) mod 8 = (5
3 + 3) mod 8 = (15 + 3) mod 8 = 18 mod 8 = 2
X3 = (5X2 + 3) mod 8 = (5
2 + 3) mod 8 = (10 + 3) mod 8 = 13 mod 8 = 5
X4 = (5X3 + 3) mod 8 = (5
5 + 3) mod 8 = (25 + 3) mod 8 = 28 mod 8 = 4
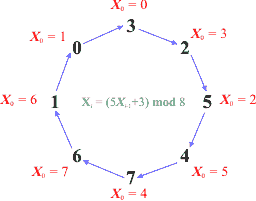
Poniżej umieściliśmy pierścień liczb pseudolosowych wygenerowanych przez ten generator. Czerwonym kolorem oznaczyliśmy punkt startowy pierścienia dla danego ziarna Xo.
Po wygenerowaniu 8 liczb pseudolosowych (ogólnie m liczb) wracamy do tej samej wartości, zatem kolejne liczby powtarzają się z okresem m. Wynika stąd wniosek, iż użyteczny generator (o ile nie służy on do specjalnych celów) powinien generować liczby z dużego przedziału wartości, np. od 0 do 232-1. Wtedy cykl obejmuje aż 4 miliardy liczb. Za dobry generator LCG przyjmuje się, zgodnie z profesorem Donaldem Knuthem, generator:
Xi = (3141592653Xi-1 + 2718281829) mod 235
Generator LCG( 235, 3141592653, 2718281829, Xo ) tworzy liczby pseudolosowe z zakresu od 0 do 235 - 1. Zwróć uwagę, iż mnożnik a jest równy części całkowitej z 109p, natomiast przyrost c jest równy części całkowitej z 109e, gdzie e - podstawa logarytmów naturalnych. Ciekawe, nieprawdaż?
Opisane generatory liniowe tworzą ciągi liczb pseudolosowych o wartościach całkowitych. W wielu zastosowaniach potrzebne są liczby losowe rzeczywiste, które powstają w zadanym przedziale. Najczęściej będzie to przedział domknięty od 0 i otwarty do 1 (inne przedziały wartości mogą być otrzymywane poprzez proste transformacje arytmetyczne, co pokażemy w dalszej części tego rozdziału).
0
L < 1, L - rzeczywista liczba pseudolosowa.
Rzeczywistą liczbę pseudolosową L leżącą w przedziale <0,1) uzyskujemy w bardzo prosty sposób z całkowitej liczby pseudolosowej wg poniższych wzorów:
Generacja rzeczywistych liczb
pseudolosowychGenerator Multiplikatywny c = 0
L = Xi - 1 m - 1 Generator Mieszany c > 0
L = Xi m Xi - nowa liczba pseudolosowa
L - liczba pseudolosowa w przedziale <0,1)
c - przyrost
m - modułAby wygenerowane rzeczywiste liczby pseudolosowe były dobrej jakości i gęsto zapełniały przedział, moduł generatora LCG musi być odpowiednio duży (co najmniej 2 miliardy).
Liniowe generatory liczb pseudolosowych są powszechnie stosowane w różnych językach programowania do tworzenia liczb pseudolosowych. Ponieważ dla danego ziarna generują one takie same ciągi pseudolosowe, w programach występuje konieczność zainicjowania generatora wartością ziarna, która będzie przy każdym uruchomieniu inna. Najczęściej stosuje się do tego celu odczyt wewnętrznego zegara działającego niezależnie od komputera. Odczytany czas przekształcany jest na liczbę całkowitą i wpisywany do zmiennej pełniącej funkcję ziarna liczb pseudolosowych. Ponieważ czasu uruchomienia programu nie da się z góry przewidzieć, jest to dobre rozwiązanie, które umożliwia zwiększenie "przypadkowości" wygenerowanych liczb pseudolosowych.
Poniżej zebraliśmy zestaw instrukcji języków programowania związanych z generacją liczb pseudolosowych.
Obsługa liczb pseudolosowych w językach wysokiego poziomu Pascal randomize - procedura wpisuje do ziarna liczb pseudolosowych wartość odczytaną z zegara systemowego. Procedurę tę wywołujemy tylko raz przed wywołaniem funkcji generujących liczby pseudolosowe.
RandSeed - zmienna typu longint przechowująca ziarno liczb pseudolosowych. Przy starcie programu inicjowana jest zawsze na 0. Dlatego należy użyć procedury Randomize, aby uzyskiwać różne ciągi liczb pseudolosowych. Zapis tej samej wartości do ziarna umożliwia generację identycznych ciągów pseudolosowych, co może być przydatne np. przy szyfrowaniu informacji zadanym kluczem.
random - funkcja generująca liczbę pseudolosową. Występuje w dwóch odmianach:
- random bez parametrów zwraca wartość zmiennoprzecinkową leżącą w przedziale <0,1).
- random(max : integer) - zwraca wartość całkowitą leżącą w przedziale od 0 do max-1
Przed pierwszym wywołaniem tej funkcji należy zainicjować ziarno liczb pseudolosowych RandSeed lub wywołać procedurę randomize.
C++ void srand(unsigned int seed) - funkcja wpisuje podaną wartość seed do ziarna liczb pseudolosowych. Najczęściej wywołuje się ją raz na początku programu z wartością odczytaną z zegara systemowego:
srand((unsigned)time(NULL));
Gwarantuje to, iż przy każdym uruchomieniu programu będzie tworzona inna sekwencja liczb pseudolosowych. Jeśli parametr seed ma wartość 1, to ziarno zostanie zainicjowane ponownie poprzednio użytą wartością argumentu wywołania srand(). Umożliwia to w prosty sposób powtórzenie ciągu wygenerowanych liczb pseudolosowych.
int rand(void) - funkcja zwraca wyliczoną wartość liczby pseudolosowej, która wpada w zakres od 0 do RAND_MAX. Stała RAND_MAX jest równa 32767 - 0x7fff. Jak widzimy, nie jest to zbyt dobry generator, lepiej skorzystać z informacji podanych w naszym opracowaniu i zaprojektować własny.
Basic RANDOMIZE n - ustawia ziarno generatora pseudolosowego na wartość n. Jeśli chcemy, aby przy każdym uruchomieniu programu komputer generował inny ciąg liczb pseudolosowych, to powinniśmy zastosować polecenie: RANDOMIZE TIMER
Liczbę pseudolosową z zakresu od <0,1) generuje funkcja RND lub RND(1).
Python W języku Python generację liczb pseudolosowych rozwiązuje moduł random. Jeśli chcemy wykorzystywać zawarte w nim funkcje i procedury (których jest bardzo wiele), to na początku programu dodajemy deklarację: import random
random.seed(n) - funkcja ustawia ziarno generatora liczb pseudolosowych na n. Jeśli argument n zostanie pominięty, to jako wartość ziarna zostanie pobrany stan zegara systemowego. Zwykle nie musimy używać tej funkcji (o ile nie chcemy rozpoczynać sekwencji pseudolosowych od zadanych wartości), ponieważ jest ona automatycznie wywoływana przy inicjalizacji modułu random.
random.random() - zwraca rzeczywistą liczbę pseudolosową z przedziału <0,1)
random.uniform(a,b) - zwraca rzeczywistą liczbę pseudolosową z przedziału <a,b)
random.randint(a,b) - zwraca całkowitą liczbę pseudolosową z przedziału <a,b>
Moduł random posiada o wiele więcej funkcji związanych z generacją liczb pseudolosowych, których opis zająłby zbyt wiele miejsca. Dlatego zainteresowanych odsyłam do odpowiedniej literatury.
JavaScript Math.random(seed) - generuje liczbę pseudolosową z ziarna seed wpadającą w przedział <0,1) Math.random() - generuje kolejną liczbę pseudolosową w przedziale <0,1).
Liniowy generator liczb pseudolosowych w JavaScript jest automatycznie inicjowany stanem zegara systemowego. Jeśli jednak chcemy mieć większą kontrolę nad jego działaniem, to w skryptach używających liczb pseudolosowych powinniśmy stosować następujący fragment kodu:
var czas = new Date();
var ziarno = czas.getSeconds();
var liczba_losowa = Math.random(ziarno);
...Poniżej zebraliśmy kilka wersji użytecznych, liniowych generatorów liczb pseudolosowych:
Przykładowe generatory liczb pseudolosowych LCG(233280,9301,49297,X), X [0...233279]
LCG(714025,4096,150889,X), X [0...714024]
LCG(231,1103515245,12345,X), X [0...231 - 1] - ANSIC
LCG( 235,3141592653,2718281829,X), X [0...235 - 1] - Knuth
Po omówieniu podstawowych metod tworzenia liczb pseudolosowych przejdziemy do ich konkretnych zastosowań.
Generacja całkowitych liczb pseudolosowych
W drodze losowania chcielibyśmy otrzymywać wartości całkowite z przedziału <a...b>, a,b ![]() C, tzn. wygenerowana liczba pseudolosowa powinna spełniać nierówność a £ X[a,b] £ b. Wszystkie liczby całkowite zawarte w przedziale <a...b> możemy zapisać jako ciąg:
C, tzn. wygenerowana liczba pseudolosowa powinna spełniać nierówność a £ X[a,b] £ b. Wszystkie liczby całkowite zawarte w przedziale <a...b> możemy zapisać jako ciąg:
a + 0, a + 1, a + 2, ... a + (b - a) - 1, a + (b - a)
Każda liczba jest więc sumą a + c, gdzie c = 0, 1, 2, 3, ..., (b - a) - 1, (b - a). Aby wylosować dowolną liczbę z tego przedziału, należy do wartości a dodać liczbę pseudolosową należącą do przedziału <0...(b - a)>. W tym celu liczbę pseudolosową otrzymaną z generatora poddajemy operacji modulo (b - a) + 1. Oczywiście zakres liczb pseudolosowych powinien być dużo większy od (b - a) + 1, w przeciwnym razie nie otrzymamy wszystkich pożądanych wartości lub rozkład przestanie być równomierny.
Ostatecznie, liczbę pseudolosową wygenerujemy w przedziale <a...b> za pomocą poniższego wzoru:
X[a,b] = a + X mod (b - a + 1)
W tabeli pokazujemy, jak wykonać tę operację w kilku wybranych językach programowania:
| Generacja liczby pseudolosowej w przedziale <a...b> | |
|---|---|
| Pascal | X[a,b] := a + random(b - a + 1); |
| C++ | X[a,b] = a + rand() % (b - a + 1); |
| Basic | X[a,b] = a + INT(RND(1) * (b - a + 1) |
| Python | X[a,b] = random.randint(a, b + 1) |
| JavaScript | X[a,b] = a + Math.floor(Math.random() * (b - a + 1)); |
Generacja rzeczywistych liczb pseudolosowych
W przypadku liczb rzeczywistych postępujemy w sposób podobny. Załóżmy, iż chcemy otrzymać liczbę pseudolosową należącą do przedziału <a,b) (domkniętego od a i otwartego od b). Każdą liczbę w tym przedziale można przedstawić w postaci sumy: a + c, c ![]() <0,(b - a))
<0,(b - a))
Z kolei liczby w przedziale <0,(b - a)) można przedstawić jako iloczyn
(b - a)d, d ![]() <0,1)
<0,1)
Wystarczy zatem wygenerować liczbę pseudolosową w przedziale <0,1), pomnożyć ją przez (b - a) i dodać a, aby otrzymać liczbę pseudolosową z przedziału <a,b):
X[a,b> = a + X<0,1) ![]() (b-a)
(b-a)
W poniższej tabeli pokazujemy, jak wykonać tę operację w kilku wybranych językach programowania:
| Generacja rzeczywistej liczby pseudolosowej w przedziale <a,b) | |
|---|---|
| Pascal | X<a,b) := a + random * (b - a); |
| C++ | X<a,b) = a + ((double)rand() / (double)(RAND_MAX+1) * (b -a); |
| Basic | X<a,b) = a + RND * (b - a) |
| Python | X<a,b) = random.uniform(a, b) |
| JavaScript | X<a,b) = a + Math.random() * (b - a); |
GNU Free Documentation License.
Źródło: mgr Jerzy Wałaszek