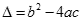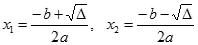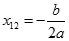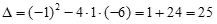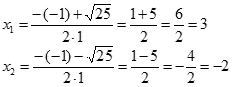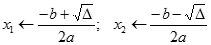JustPaste.it

Miejsca zerowe funkcji - Równania wielomianowe

3903bcb18e96be5b42f5d0c72c7bfdfe.gif

Równanie kwadratowe posiada następującą postać:

ax2 + bx + c = 0,  a 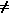5e71e4f629ad4e71a77fa74767ea1d6a.gif 0

gdzie x to poszukiwana niewiadoma, a a, b, c to współczynniki równania. Pierwiastkiem równania jest taka wartość niewiadomej x, która podstawiona w jej miejsce do równania spełnia je. Zwykle równanie kwadratowe posiada dwa pierwiastki rzeczywiste (lub zespolone - nie będziemy się nimi zajmować). Jeśli istnieje tylko jedna taka liczba, to mówimy, iż jest ona pierwiastkiem podwójnym.

a152a6c4fb2ef4fa0223014e65f74f79.gif

Pierwiastkami równania kwadratowego x2 - x - 6 = 0 są dwie liczby x1 = 3 i x2 = -2, ponieważ:

(x1)2 - (x1) - 6 = 32 - 3 - 6 = 9 - 3 - 6 = 0 - równanie jest spełnione

(x2)2 - (x2) - 6 = (-2)2 - (-2) - 6 = 4 + 2 - 6 = 0 - równanie jest spełnione

Matematycy opracowali na przestrzeni wieków rozwoju matematyki wiele metod rozwiązywania równań kwadratowych. My wykorzystamy metodę "szkolną", którą powinien doskonale znać uczeń liceum.

Obliczamy wyróżnik równania kwadratowego Δ:

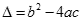
c7ec2d51af1040aa021210eec3aac9ee.gif

W zależności od wartości wyróżnika Δ mamy trzy możliwe przypadki:

1. Δ > 0, istnieją dwa pierwiastki rzeczywiste:

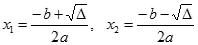
da223d799786de5a20932580490688ce.gif

2. Δ = 0, istnieje jeden pierwiastek podwójny:

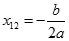
3573d657a7b4db4c2f488b71000391d4.gif

3. Δ < 0, nie istnieją pierwiastki rzeczywiste (równanie posiada jedynie pierwiastki zespolone, które są liczbami sprzężonymi).

a152a6c4fb2ef4fa0223014e65f74f79.gif

Rozwiążmy podaną metodą równanie z poprzedniego przykładu:

x2 - x - 6 = 0

a = 1,  b = -1,  c = -6

Obliczamy wyróżnik Δ: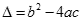

c7ec2d51af1040aa021210eec3aac9ee.gif

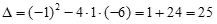
33fc33cc72ffff0bf50cb9165dce76c9.gif

Wyróżnik Δ jest większy od 0, zatem równanie posiada dwa pierwiastki rzeczywiste: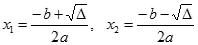

da223d799786de5a20932580490688ce.gif

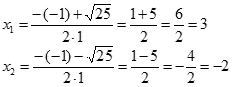
850aaeb5b4d7475ad795415a2403c619.gif

3c0b30d1f9266443d0a5c9eda139b227.gif

Dane wejściowe

a, b, c - współczynniki równania kwadratowego. a,b,c a7c7918756762daecbfdef28cc40abba.gif R

Dane wyjściowe

x1, x2 - pierwiastki równania kwadratowego lub informacja, iż równanie nie posiada pierwiastków rzeczywistych.
x1, x2 a7c7918756762daecbfdef28cc40abba.gif R

Zmienne pomocnicze i funkcje

Δ - wyróżnik równania kwadratowego. Δ a7c7918756762daecbfdef28cc40abba.gif R
ε - określa dokładność porównania z zerem. ε = 0.0000000001
a3011067ac9671597a79d74dede9f39b.gif
krok 1: Odczytaj współczynniki a, b, c
krok 2: Jeśli | a | < ε, pisz "To nie jest równanie kwadratowe" i zakończ algorytm
krok 3: Δ 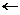3f1f8f17e2fd6e997a73f31a61399b79.gif b2 - 4ac
krok 4: Jeśli | Δ | < ε, to Δ 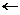3f1f8f17e2fd6e997a73f31a61399b79.gif 0
krok 5: Jeśli Δ < 0, pisz "Brak pierwiastków rzeczywistych" i zakończ algorytm
krok 6: 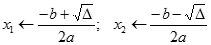20efb3c8da1c77364f94734e3dd45e93.gif
krok 7: Pisz x1, x2 i zakończ algorytm

8b64130616b0d56aedd67377a1d36a42.gif

 

Algorytm obliczania pierwiastków równania kwadratowego rozpoczynamy od wczytania wartości współczynników a, b oraz c.

Jeśli współczynnik a przy x2 wynosi 0 (wpada w otoczenie 0 o promieniu ε) to nie mamy do czynienia z równaniem kwadratowym. Wypisujemy odpowiedni komunikat i kończymy algorytm.

Obliczamy wyróżnik Δ. Następnie sprawdzamy, czy Δ jest w otoczeniu ε zera. Jeśli tak, to zerujemy go - w ten sposób uprościmy znacznie algorytm.

Kolejny test sprawdza, czy wyróżnik Δ jest mniejszy od zera (kolejność testów jest tutaj bardzo ważna). Jeśli tak, to równanie nie posiada pierwiastków rzeczywistych. Wypisujemy odpowiedni komunikat i kończymy algorytm.

Pozostał przypadek, gdy wyróżnik Δ jest albo równy, albo większy od 0. W obu przypadkach obliczamy dwa pierwiastki x1 i x2. Wypisujemy je i kończymy algorytm.


be8afe1eb394d868f43b35c3207adc14.gif

0fa0a2049bc53a82957ad6f82f72a48e.gif    
   
   

0c4c19a59ae8b7752785fdfec58e674f.gif

Poniższe, przykładowe programy są praktyczną realizacją omawianego w tym rozdziale algorytmu. Zapewne można je napisać bardziej efektywnie. To już twoje zadanie. Dokładny opis stosowanych środowisk programowania znajdziesz we wstępie. Programy przed opublikowaniem w serwisie edukacyjnym zostały dokładnie przetestowane. Jeśli jednak znajdziesz jakąś usterkę (co zawsze może się zdarzyć), to prześlij o niej informację do autora. Pozwoli to ulepszyć nasze artykuły. Będziemy Ci za to wdzięczni.

  
       

Programy wczytują wartości współczynników a, b i c, a następnie wyznaczają, o ile jest to możliwe, pierwiastki równania kwadratowego o wprowadzonych współczynnikach.

Wydruk z uruchomionego programu 
Demonstracja rozwiązywania równania kwadratowego:
ax^2 + bx + c = 0
-------------------------------------------------
(C)2006 mgr Jerzy Wałaszek        I LO w Tarnowie

Podaj kolejno współczynniki a,b i c:

a = 1
b = -1
c = -6

-------------------------------------------------

WYNIKI:

x1 =      3,00000
x2 =     -2,00000

-------------------------------------------------
Koniec. Naciśnij klawisz Enter...
Microsoft Visual Basic 2005 Express Edition

 

Borland
Delphi 7.0
Personal
Edition		 
// Program rozwiązuje równanie kwadratowe
//---------------------------------------
// (C)2006 mgr J.Wałaszek I LO w Tarnowie

program mzfk1;

{$APPTYPE CONSOLE}

const
  EPS   = 0.0000000001; // dokładność porównania z zerem
var
  a,b,c,delta,x1,x2 : real;
begin
  writeln('Demonstracja rozwiazywania rownania kwadratowego:');
  writeln('ax^2 + bx + c = 0');
  writeln('-------------------------------------------------');
  writeln('(C)2006 mgr Jerzy Walaszek        I LO w Tarnowie');
  writeln;
  writeln('Podaj kolejno wspolczynniki a,b i c:');
  writeln;
  write('a = '); readln(a);
  write('b = '); readln(b);
  write('c = '); readln(c);
  writeln;
  writeln('-------------------------------------------------');
  writeln;
  writeln('WYNIKI:');
  writeln;
  if abs(a) < EPS then
    writeln('To nie jest rownanie kwadratowe')
  else
  begin
    delta := b * b - 4 * a * c;
    if abs(delta) < EPS then delta := 0;
    if delta < 0 then
      writeln('Brak pierwiastkow rzeczywistych')
    else
    begin
      x1 := (-b + sqrt(delta)) / 2 / a;
      x2 := (-b - sqrt(delta)) / 2 / a;
      writeln('x1 = ',x1:12:5);
      writeln('x2 = ',x2:12:5);
    end;
  end;
  writeln;
  writeln('-------------------------------------------------');
  writeln('Koniec. Nacisnij klawisz Enter...');
  readln;
end.
Borland
C++ Builder
6.0
Personal
Edition		 
// Program rozwiązuje równanie kwadratowe
//---------------------------------------
// (C)2006 mgr J.Wałaszek I LO w Tarnowie

#include <iostream>
#include <iomanip>
#include <cmath>

using namespace std;

int main(int argc, char* argv[])
{
  const double EPS   = 0.0000000001; // dokładność porównania z zerem

  double a,b,c,delta,x1,x2;

  cout.precision(5);     // 5 cyfr po przecinku
  cout.setf(ios::fixed); // format stałoprzecinkowy

  cout << "Demonstracja rozwiazywania rownania kwadratowego:\n"
          "ax^2 + bx + c = 0\n"
          "-------------------------------------------------\n"
          "(C)2006 mgr Jerzy Walaszek        I LO w Tarnowie\n\n"
          "Podaj kolejno wspolczynniki a,b i c:\n\n";
  cout << "a = "; cin >> a;
  cout << "b = "; cin >> b;
  cout << "c = "; cin >> c;
  cout << "\n-------------------------------------------------\n\n"
          "WYNIKI:\n\n";
  if(fabs(a) < EPS)
    cout << "To nie jest rownanie kwadratowe\n";
  else
  {
    delta = b * b - 4 * a * c;
    if(fabs(delta) < EPS) delta = 0;
    if(delta < 0)
      cout << "Brak pierwiastkow rzeczywistych\n";
    else
    {
      x1 = (-b + sqrt(delta)) / 2 / a;
      x2 = (-b - sqrt(delta)) / 2 / a;
      cout << "x1 = " << setw(12) << x1 << endl
           << "x2 = " << setw(12) << x2 << endl;
    }
  }
  cout << "\n------------------------------------------------\n";
  system("pause");
  return 0;
}
Microsoft
Visual
Basic 2005
Express
Edition		 
' Program rozwiązuje równanie kwadratowe
'---------------------------------------
' (C)2006 mgr J.Wałaszek I LO w Tarnowie

Module Module1

  Sub Main()

    Const EPS = 0.0000000001   ' dokładność porównania z zerem

    Dim a, b, c, delta, x1, x2 As Double
    
    Console.WriteLine("Demonstracja rozwiązywania równania kwadratowego:")
    Console.WriteLine("ax^2 + bx + c = 0")
    Console.WriteLine("-------------------------------------------------")
    Console.WriteLine("(C)2006 mgr Jerzy Wałaszek        I LO w Tarnowie")
    Console.WriteLine()
    Console.WriteLine("Podaj kolejno współczynniki a,b i c:")
    Console.WriteLine()
    Console.Write("a = ") : a = Val(Console.ReadLine)
    Console.Write("b = ") : b = Val(Console.ReadLine)
    Console.Write("c = ") : c = Val(Console.ReadLine)
    Console.WriteLine()
    Console.WriteLine("-------------------------------------------------")
    Console.WriteLine()
    Console.WriteLine("WYNIKI:")
    Console.WriteLine()
    If Math.Abs(a) < EPS Then
      Console.WriteLine("To nie jest równanie kwadratowe")
    Else
      delta = b * b - 4 * a * c
      If Math.Abs(delta) < EPS Then delta = 0
      If delta < 0 Then
        Console.WriteLine("Brak pierwiastków rzeczywistych")
      Else
        x1 = (-b + Math.Sqrt(delta)) / 2 / a
        x2 = (-b - Math.Sqrt(delta)) / 2 / a
        Console.WriteLine("x1 = {0,12:F5}", x1)
        Console.WriteLine("x2 = {0,12:F5}", x2)
      End If
    End If
    Console.WriteLine()
    Console.WriteLine("-------------------------------------------------")
    Console.WriteLine("Koniec. Naciśnij klawisz Enter...")
    Console.ReadLine()
  End Sub

End Module
Python 
# -*- coding: cp1250 -*-
# Program rozwiązuje równanie kwadratowe
#---------------------------------------
# (C)2006 mgr J.Wałaszek I LO w Tarnowie

import math

EPS   = 0.0000000001   # dokładność porównania z zerem

print "Demonstracja rozwiazywania rownania kwadratowego:"
print "ax^2 + bx + c = 0"
print "-------------------------------------------------"
print "(C)2006 mgr Jerzy Walaszek        I LO w Tarnowie"
print
print "Podaj kolejno wspolczynniki a,b i c:"
print
a = float(raw_input("a = "))
b = float(raw_input("b = "))
c = float(raw_input("c = "))
print
print "-------------------------------------------------"
print
print "WYNIKI:"
print
if abs(a) < EPS:
  print "To nie jest rownanie kwadratowe"
else:
  delta = b * b - 4 * a * c
  if abs(delta) < EPS: delta = 0
  if delta < 0:
    print "Brak pierwiastkow rzeczywistych"
  else:
    x1 = (-b + math.sqrt(delta)) / 2 / a
    x2 = (-b - math.sqrt(delta)) / 2 / a
    print "x1 = %12.5f" % x1
    print "x2 = %12.5f" % x2
print
print "---------------------------------------------------------"
raw_input("Koniec. Nacisnij klawisz Enter...")
JavaScript 
<html>
  <head>
  </head>
  <body>
    <div align="center">
      <form style="BORDER-RIGHT: #ff9933 1px outset; PADDING-RIGHT: 4px;
                   BORDER-TOP: #ff9933 1px outset; PADDING-LEFT: 4px;
                   PADDING-BOTTOM: 1px; BORDER-LEFT: #ff9933 1px outset;
                   PADDING-TOP: 1px; BORDER-BOTTOM: #ff9933 1px outset;
                   BACKGROUND-COLOR: #ffcc66" name="frmbincode">
        <h3 style="TEXT-ALIGN: center">
          Demonstracja rozwiązywania równania kwadratowego
        </h3>
        <p style="TEXT-ALIGN: center">
          <i>ax<sup>2</sup> + bx + c = 0</i>
        </p>
        <p style="TEXT-ALIGN: center">
          (C)2006 mgr Jerzy Wałaszek I LO w Tarnowie
        </p>
        <hr>
        <p style="text-align: center">
          Wpisz do pól edycyjnych kolejne współczynniki równania
        </p>
        <div align="center">
          <table border="0" id="table146" cellpadding="8"
                 style="border-collapse: collapse">
            <tr>
              <td>
                a = <input type="text" name="wsp_a" size="15" value="1"
                           style="text-align: right">
              </td>
              <td>
                b = <input type="text" name="wsp_b" size="15" value="-1"
                           style="text-align: right">
              </td>
              <td>
                c = <input type="text" name="wsp_c" size="15" value="-6"
                           style="text-align: right">
               </td>
               <td>
                 <input type="button" value="Rozwiąż równanie" name="B1"
                        onclick="main()">
               </td>
             </tr>
           </table>
         </div>
         <div id="out" align="center">...</div>
       </form>

<script language=javascript>

// Program rozwiązuje równanie kwadratowe
//---------------------------------------
// (C)2006 mgr J.Wałaszek I LO w Tarnowie

function main()
{
  var EPS = 0.0000000001; // dokładność porównania z zerem
  var a,b,c,delta,x1,x2,t;

  a = parseFloat(document.frmbincode.wsp_a.value);
  b = parseFloat(document.frmbincode.wsp_b.value);
  c = parseFloat(document.frmbincode.wsp_c.value);
  if(isNaN(a) || isNaN(b) || isNaN(c))
    t = "<font color=red><b>Nieprawidłowe współczynniki!</b></font>";
  else if(Math.abs(a) < EPS)
    t = "<font color=red><b>To nie jest rownanie kwadratowe</b></font>";
  else
  {
    delta = b * b - 4 * a * c;
    if(Math.abs(delta) < EPS) delta = 0;
    if(delta < 0)
      t = "<font color=red><b>Brak pierwiastkow rzeczywistych</b></font>";
    else
    {
      x1 = (-b + Math.sqrt(delta)) / 2 / a;
      x2 = (-b - Math.sqrt(delta)) / 2 / a;
      t = "x<sub>1</sub> = " + x1 + "<BR>x<sub>2</sub> = " + x2;
    }
  }
  document.getElementById("out").innerHTML = t;
}

</script>
    </div>
  </body>
</html>
 
 
Dokument ten rozpowszechniany jest zgodnie z zasadami licencji
GNU Free Documentation License.
   document.frmadminemail.adminemail_tytul.value = parent.document.title + " : " + document.title;  

 

Źródło: mgr Jerzy Wałaszek

technologia programowanie