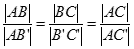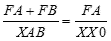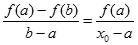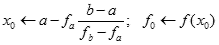Mamy daną funkcję f(x) oraz przedział <a,b> poszukiwań pierwiastka. W przedziale tym funkcja musi spełniać następujące warunki:
- Funkcja f(x) jest określona - dla każdej wartości argumentu x z przedziału <a,b> potrafimy policzyć wartość funkcji.
- Funkcja f(x) jest ciągła - jej wartości nie "wykonują" nagłych skoków. Funkcja przebiega przez wszystkie wartości pośrednie - nie istnieją zatem przerwy w kolejnych wartościach funkcji.
- Funkcja f(x) na krańcach przedziału <a,b> przyjmuje różne znaki. Ponieważ funkcja, zgodnie z poprzednim wymogiem, jest ciągła, to przyjmuje w przedziale <a,b> wszystkie wartości pośrednie pomiędzy f(a) i f(b). Wartości te mają różne znaki (czyli leżą po różnych stronach osi OX), zatem musi być taki punkt xo w przedziale <a,b>, dla którego funkcja przyjmuje wartość pośrednią:
f(a) < f(xo) = 0 < f(b) lub f(a) > f(xo) = 0 > f(b)
Gdy funkcja f(x) spełnia podane warunki, to w przedziale <a,b> zagwarantowane jest istnienie pierwiastka i możemy go wyszukać algorytmem regula falsi.
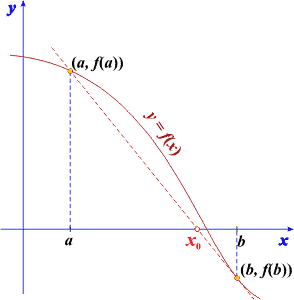
W języku łacińskim regula falsi oznacza fałszywą prostą. Ideą tej metody jest założenie, iż funkcja w coraz mniejszych przedziałach wokół pierwiastka zaczyna przypominać funkcję liniową. Skoro tak, to przybliżenie pierwiastka otrzymujemy prowadząc linię prostą (sieczną) z punktów krańcowych przedziału. Sieczna przecina oś OX w punkcie xo, który przyjmujemy za przybliżenie pierwiastka - gdyby funkcja faktycznie była liniowa, otrzymany punkt xo byłby rzeczywistym pierwiastkiem.
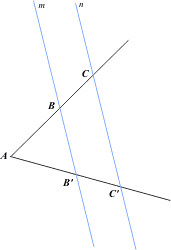
Wzór dla xo można wyprowadzić na kilka sposobów. My wybierzemy znane twierdzenie Talesa, które mówi, iż jeżeli ramiona kąta przetniemy dwiema prostymi równoległymi, to długości odcinków wyznaczonych przez te proste na jednym ramieniu kąta będą proporcjonalne do długości odpowiednich odcinków wyznaczonych przez te proste na ramieniu drugim. Poniższy rysunek obrazuje tę sytuację:
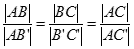
W naszym przypadku postępujemy następująco:
Kąt utworzą odpowiednie odcinki:
pionowo FA = (a,0)-(a,f(a)) powiększony o odcinek FB = (b,0)-(b,-f(b))
poziomo XAB = (a,0)-(b,0)
Prostymi równoległymi będzie cięciwa z punktów krańcowych przedziału, oraz ta sama cięciwa przesunięta pionowo w górę o długość odcinka FB.
Poniższy rysunek obrazuje otrzymaną sytuację:
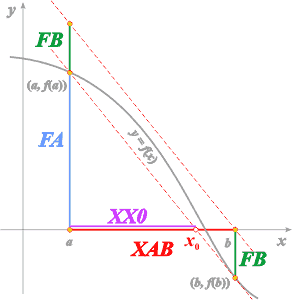
Zgodnie z twierdzeniem Talesa mamy:
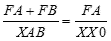
Jeśli podstawimy do tego wzoru długości odcinków:
FA = f(a)
FB = -f(b)
XAB = b - a
XX0 = xo - a
Otrzymamy:
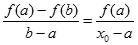
a dalej:
Ostatnie przekształcenie ma na celu otrzymanie wzoru o lepszej "zapamiętywalności". Mnożymy mianownik przez (-1), dzięki czemu staje się on spójny z licznikiem ułamka. Sam ułamek zmienia znak na minus.
Algorytm regula falsi jest bardzo podobny do opisanego w poprzednim rozdziale algorytmu bisekcji. Założenia wstępne dla badanej funkcji w obu algorytmach są identyczne. Różnią się one sposobem wyznaczania punktu xo. W algorytmie bisekcji punkt ten zawsze wyznaczany był w środku przedziału <a,b>. Z tego powodu algorytm bisekcji jest "nieczuły" na przebieg funkcji - zawsze zbliża się do pierwiastka w ten sam sposób.
W algorytmie regula falsi jest inaczej. Punk xo wyznaczany jest w zależności od wartości funkcji na krańcach przedziału poszukiwań. W efekcie w każdej iteracji otrzymujemy lepsze przybliżenie do rzeczywistej wartości pierwiastka. Zatem w większości przypadków algorytm regula falsi szybciej osiągnie założoną dokładność pierwiastka od algorytmu bisekcji (chociaż można oczywiście podać kontrprzykłady).
Po wyznaczeniu przybliżonego pierwiastka postępowanie w obu algorytmach jest w zasadzie takie samo. Sprawdzamy, czy wartość modułu różnicy pomiędzy dwoma ostatnimi przybliżeniami pierwiastka jest mniejsza od zadanego minimum. Jeśli tak, obliczenia kończymy zwracając xo.
Obliczamy wartość funkcji w punkcie xo i sprawdzamy, czy jest ona dostatecznie bliska zeru. Jeśli tak, zwracamy xo i kończymy. Jeśli nie, za nowy przedział przyjmujemy tą część przedziału <a,b> rozdzielonego przez xo, w której funkcja zmienia znak. Całą procedurę powtarzamy, aż do osiągnięcia pożądanego wyniku.

Dane wejściowe
| f(x) | - | funkcja, której pierwiastek liczymy. Musi spełniać warunki podane na początku tego rozdziału. |
| a,b | - | punkty krańcowe przedziału poszukiwań pierwiastka funkcji f(x). a,b  R R |
Dane wyjściowe
| xo | - | pierwiastek funkcji f(x) |
Zmienne pomocnicze i funkcje
| fa , fb , fo | - wartości funkcji odpowiednio w punktach a, b, xo. fa , fb , fo  R R |
| x1 | - przechowuje poprzednią wartość przybliżenia xo |
| εo | - określa dokładność porównania z zerem. εo = 0.0000000001 |
| εx | - określa dokładność wyznaczania pierwiastka xo. εx = 0.0000000001 |

| | krok 1: | Odczytaj a i b |
| | krok 2: | fa 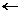 f(a) ; fb f(a) ; fb 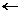 f(b); x1 f(b); x1  a; xo a; xo  b b |
| | krok 3: | Jeśli fa  fb > 0, pisz "Funkcja nie spełnia założeń" i zakończ algorytm fb > 0, pisz "Funkcja nie spełnia założeń" i zakończ algorytm |
| | krok 4: | Dopóki | x1 - xo | > εx: wykonuj kroki 5 ... 8 |
| krok 5: | x1  xo xo |
| krok 6: | 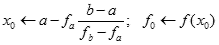 |
| krok 7: | Jeśli | fo | < εo, to idź do kroku 9 |
| krok 8: | Jeśli fa  fo < 0, to b fo < 0, to b 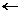 xo; fb xo; fb 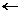 fo , inaczej a fo , inaczej a 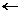 xo; fa xo; fa 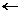 fo fo |
| | krok 9: | Pisz xo i zakończ algorytm |

Algorytm regula falsi jest bardzo podobny do algorytmu bisekcji. Zmiany zaznaczono na schemacie blokowym zielonym kolorem elementów.
Odczytujemy zakres poszukiwań pierwiastka danej funkcji. W zmiennych fa i fb umieszczamy wartość funkcji na krańcach tego zakresu. Inicjujemy x1 oraz xo tak, aby algorytm nie zatrzymał się przy pierwszym obiegu pętli.
Pierwszy test ma na celu sprawdzenie warunku różnych znaków wartości funkcji na krańcach przedziału <a,b>. Różne znaki gwarantują nam istnienie pierwiastka w danym zakresie. Jeśli funkcja na krańcach ma ten sam znak, wypisujemy odpowiedni komunikat i kończymy algorytm.
Rozpoczynamy pętlę wyliczania kolejnych przybliżeń pierwiastka funkcji. Pętla wykonywana jest do momentu, gdy dwa ostatnio obliczone pierwiastki różnią się o εx.
Na początku pętli do x1 wprowadzamy poprzednio wyliczony pierwiastek i obliczamy nowy. Następne obliczamy wartość funkcji w xo umieszczając ją w zmiennej fo. Sprawdzamy, czy wartość fo jest dostatecznie bliska zeru (wpada w otoczenie zera o promieniu εo), Jeśli tak, to przerywamy pętlę, co spowoduje wypisanie xo i zakończenie algorytmu.
Za nowy przedział <a,b> przyjmujemy tę część przedziału podzielonego przez xo, w której funkcja zmienia znak. Testujemy iloczyn fa przez fo. Jeśli jest ujemny, to funkcja zmienia znak przyjmuje w <a,xo>. Za nowy koniec b przyjmujemy xo i kontynuujemy pętlę. W przeciwnym razie zmiana znaku występuje w <xo,b>. Za nowy początek a przyjmujemy xo i kontynuujemy pętlę. W obu przypadkach przepisujemy również fo odpowiednio do fa lub fb w celu uniknięcia ponownych obliczeń wartości funkcji w nowych punktach krańcowych przedziału.

 | | |
| | |
| | | 
Poniższe, przykładowe programy są praktyczną realizacją omawianego w tym rozdziale algorytmu. Zapewne można je napisać bardziej efektywnie. To już twoje zadanie. Dokładny opis stosowanych środowisk programowania znajdziesz we wstępie. Programy przed opublikowaniem w serwisie edukacyjnym zostały dokładnie przetestowane. Jeśli jednak znajdziesz jakąś usterkę (co zawsze może się zdarzyć), to prześlij o niej informację do autora. Pozwoli to ulepszyć nasze artykuły. Będziemy Ci za to wdzięczni. | |
| | | | |
Programy wyznaczają miejsce zerowe funkcji:
f(x) = x3(x + sin(x2 - 1) - 1) - 1
Pierwiastków należy poszukiwać w przedziałach <-1,0> i <1,2>.
| Wydruk z uruchomionego programu |
Obliczanie pierwiastka funkcji - metoda regula falsi
f(x) = x^3*(x+sin(x^2-1)-1)-1
----------------------------------------------------
(C)2006 mgr Jerzy Wałaszek I LO w Tarnowie
Podaj zakres poszukiwań pierwiastka:
a = 1
b = 2
----------------------------------------------------
WYNIK:
x0 = 1,18983299
----------------------------------------------------
Koniec. Naciśnij klawisz Enter... |
| Microsoft Visual Basic 2005 Express Edition |
Borland
Delphi 7.0
Personal
Edition | // Program znajduje miejsce zerowe funkcji f(x)
// za pomocą algorytmu regula falsi
//---------------------------------------------
// (C)2006 mgr J.Wałaszek I LO w Tarnowie
program mzf1;
{$APPTYPE CONSOLE}
uses math;
const
EPS0 = 0.0000000001; // dokładność porównania z zerem
EPSX = 0.0000000001; // dokładność wyznaczenia pierwiastka
// Funkcja, której miejsce zerowe obliczamy
// f(x) = x^3*(x+sin(x^2-1)-1)-1
// <-1,0> i <1,2>
//-----------------------------------------
function f(x : real) : real;
begin
Result := x * x * x * (x + sin(x * x - 1) - 1) - 1;
end;
//-----------------------------------------------------
// Program główny
//-----------------------------------------------------
var
a,b,x0,x1,fa,fb,f0 : real;
begin
writeln('Obliczanie pierwiastka funkcji - metoda regula falsi');
writeln('f(x) = x^3*(x+sin(x^2-1)-1)-1');
writeln('----------------------------------------------------');
writeln('(C)2006 mgr Jerzy Walaszek I LO w Tarnowie');
writeln;
writeln('Podaj zakres poszukiwan pierwiastka:');
writeln;
write('a = '); readln(a);
write('b = '); readln(b);
writeln;
writeln('----------------------------------------------------');
writeln('WYNIK:');
writeln;
fa := f(a); fb := f(b); x1 := a; x0 := b;
if fa * fb > 0 then writeln('Funkcja nie spelnia zalozen')
else
begin
while abs(x1 - x0) > EPSX do
begin
x1 := x0;
x0 := a - fa * (b - a) / (fb - fa);
f0 := f(x0);
if abs(f0) < EPS0 then break;
if fa * f0 < 0 then
begin
b := x0; fb := f0;
end
else
begin
a := x0; fa := f0;
end;
end;
writeln('x0 = ',x0:15:8);
end;
writeln;
writeln('----------------------------------------------------');
writeln('Koniec. Nacisnij klawisz Enter...');
readln;
end. |
Borland
C++ Builder
6.0
Personal
Edition | // Program znajduje miejsce zerowe funkcji f(x)
// za pomocą algorytmu regula falsi
//---------------------------------------------
// (C)2006 mgr J.Wałaszek I LO w Tarnowie
#include <iostream>
#include <iomanip>
#include <math>
using namespace std;
const double EPS0 = 0.0000000001; // dokładność porównania z zerem
const double EPSX = 0.0000000001; // dokładność wyznaczenia pierwiastka
// Funkcja, której miejsce zerowe obliczamy
// f(x) = x^3*(x+sin(x^2-1)-1)-1
// <-1,0> i <1,2>
//-----------------------------------------
double f(double x)
{
return x * x * x * (x + sin(x * x - 1) - 1) - 1;
}
//-----------------------------------------------------
// Program główny
//-----------------------------------------------------
int main(int argc, char* argv[])
{
double a,b,x0,x1,fa,fb,f0;
cout.precision(8); // 8 cyfr po przecinku
cout.setf(ios::fixed); // format stałoprzecinkowy
cout << "Obliczanie pierwiastka funkcji - metoda regula falsi\n"
"f(x) = x^3*(x+sin(x^2-1)-1)-1\n"
"----------------------------------------------------\n"
"(C)2006 mgr Jerzy Walaszek I LO w Tarnowie\n\n"
"Podaj zakres poszukiwan pierwiastka:\n\n";
cout << "a = "; cin >> a;
cout << "b = "; cin >> b;
cout << "\n----------------------------------------------------\n\n"
"WYNIK:\n\n";
fa = f(a); fb = f(b); x1 = a; x0 = b;
if(fa * fb > 0) cout << "Funkcja nie spelnia zalozen\n";
else
{
while(fabs(x1 - x0) > EPSX)
{
x1 = x0;
x0 = a - fa * (b - a) / (fb - fa);
f0 = f(x0);
if(fabs(f0) < EPS0) break;
if(fa * f0 < 0)
{
b = x0; fb = f0;
}
else
{
a = x0; fa = f0;
}
}
cout << "x0 = " << setw(15) << x0 << endl;
}
cout << "\n------------------------------------------------\n";
system("pause");
return 0;
} |
Microsoft
Visual
Basic 2005
Express
Edition | ' Program znajduje miejsce zerowe funkcji f(x)
' za pomocą algorytmu regula falsi
'---------------------------------------------
' (C)2006 mgr J.Wałaszek I LO w Tarnowie
Module Module1
Const EPS0 = 0.0000000001 ' dokładność porównania z zerem
Const EPSX = 0.0000000001 ' dokładność wyznaczenia pierwiastka
' Funkcja, której miejsce zerowe obliczamy
' f(x) = x^3*(x+sin(x^2-1)-1)-1
' <-1,0> i <1,2>
'-----------------------------------------
Function f(ByVal x As Double) As Double
Return x * x * x * (x + Math.Sin(x * x - 1) - 1) - 1
End Function
'-----------------------------------------------------
' Program główny
'-----------------------------------------------------
Sub Main()
Dim a, b, x0, x1, fa, fb, f0 As Double
Console.WriteLine("Obliczanie pierwiastka funkcji - metoda regula falsi")
Console.WriteLine("f(x) = x^3*(x+sin(x^2-1)-1)-1")
Console.WriteLine("----------------------------------------------------")
Console.WriteLine("(C)2006 mgr Jerzy Wałaszek I LO w Tarnowie")
Console.WriteLine()
Console.WriteLine("Podaj zakres poszukiwań pierwiastka:")
Console.WriteLine()
Console.Write("a = ") : a = Val(Console.ReadLine)
Console.Write("b = ") : b = Val(Console.ReadLine)
Console.WriteLine()
Console.WriteLine("----------------------------------------------------")
Console.WriteLine()
Console.WriteLine("WYNIK:")
Console.WriteLine()
fa = f(a) : fb = f(b) : x1 = a : x0 = b
If fa * fb > 0 Then
Console.WriteLine("Funkcja nie spełnia założeń")
Else
While Math.Abs(x1 - x0) > EPSX
x1 = x0
x0 = a - fa * (b - a) / (fb - fa)
f0 = f(x0)
If Math.Abs(f0) < EPS0 Then Exit While
If fa * f0 < 0 Then
b = x0 : fb = f0
Else
a = x0 : fa = f0
End If
End While
Console.WriteLine("x0 = {0,15:F8}", x0)
End If
Console.WriteLine()
Console.WriteLine("----------------------------------------------------")
Console.WriteLine("Koniec. Naciśnij klawisz Enter...")
Console.ReadLine()
End Sub
End Module |
| Python | # -*- coding: cp1250 -*-
# Program znajduje miejsce zerowe funkcji f(x)
# za pomocą algorytmu regula falsi
#---------------------------------------------
# (C)2006 mgr J.Wałaszek I LO w Tarnowie
import math
EPS0 = 0.0000000001 # dokładność porównania z zerem
EPSX = 0.0000000001 # dokładność wyznaczenia pierwiastka
# Funkcja, której miejsce zerowe obliczamy
# f(x) = x^3*(x+sin(x^2-1)-1)-1
# <-1,0> i <1,2>
#-----------------------------------------
def f(x):
return x * x * x * (x + math.sin(x * x - 1) - 1) - 1
#-----------------------------------------------------
# Program główny
#-----------------------------------------------------
print "Obliczanie pierwiastka funkcji - metoda regula falsi"
print "f(x) = x^3*(x+sin(x^2-1)-1)-1"
print "----------------------------------------------------"
print "(C)2006 mgr Jerzy Walaszek I LO w Tarnowie"
print
print "Podaj zakres poszukiwan pierwiastka:"
print
a = float(raw_input("a = "))
b = float(raw_input("b = "))
print
print "-----------------------------------------------------"
print
print "WYNIK:"
print
fa, fb, x1, x0 = f(a), f(b), a, b
if fa * fb > 0: print "Funkcja nie spelnia zalozen"
else:
while abs(x1 - x0) > EPSX:
x1 = x0
x0 = a - fa * (b - a) / (fb - fa)
f0 = f(x0)
if abs(f0) < EPS0: break
if fa * f0 < 0: b, fb = x0, f0
else: a, fa = x0, f0
print "x0 = %15.8f" % x0
print
print "-----------------------------------------------------"
raw_input("Koniec. Nacisnij klawisz Enter...") |
| JavaScript | <html>
<head>
</head>
<body>
<div align="center">
<form style="BORDER-RIGHT: #ff9933 1px outset; PADDING-RIGHT: 4px;
BORDER-TOP: #ff9933 1px outset; PADDING-LEFT: 4px;
PADDING-BOTTOM: 1px; BORDER-LEFT: #ff9933 1px outset;
PADDING-TOP: 1px; BORDER-BOTTOM: #ff9933 1px outset;
BACKGROUND-COLOR: #ffcc66" name="frmbincode">
<h3 style="TEXT-ALIGN: center">
Obliczanie pierwiastka funkcji metodą regula falsi
</h3>
<p style="TEXT-ALIGN: center">
<i>f(x) = x<sup>3</sup>(x + sin(x<sup>2</sup> - 1) - 1) - 1</i>
</p>
<p style="TEXT-ALIGN: center">
(C)2006 mgr Jerzy Wałaszek I LO w Tarnowie
</p>
<hr>
<p style="text-align: center">
Wpisz do pól edycyjnych zakres przedziału poszukiwań pierwiastka
</p>
<div align="center">
<table border="0" id="table144" cellpadding="8"
style="border-collapse: collapse">
<tr>
<td>
a = <input type="text" name="wsp_a" size="20" value="1"
style="text-align: right">
</td>
<td>
b = <input type="text" name="wsp_b" size="20" value="2"
style="text-align: right">
</td>
<td>
<input type="button" value="Szukaj pierwiastka" name="B1"
onclick="main()">
</td>
</tr>
</table>
</div>
<div id="out" align=center>...</div>
</form>
<script language=javascript>
// Program znajduje miejsce zerowe funkcji f(x)
// za pomocą algorytmu regula falsi
//---------------------------------------------
// (C)2006 mgr J.Wałaszek I LO w Tarnowie
var EPS0 = 0.0000000001; // dokładność porównania z zerem
var EPSX = 0.0000000001; // dokładność wyznaczenia pierwiastka
// Funkcja, której miejsce zerowe obliczamy
// f(x) = x^3*(x+sin(x^2-1)-1)-1
// <-1,0> i <1,2>
//-----------------------------------------
function f(x)
{
return x * x * x * (x + Math.sin(x * x - 1) - 1) - 1;
}
//-----------------------------------------------------
// Program główny
//-----------------------------------------------------
function main()
{
var a,b,x0,x1,fa,fb,f0,t;
a = parseFloat(document.frmbincode.wsp_a.value);
b = parseFloat(document.frmbincode.wsp_b.value);
if(isNaN(a) || isNaN(b))
t = "<font color=red><b>Złe krańce zakresu poszukiwań pierwiastka!</b></font>";
else
{
t = "x<sub>o</sub> = ";
fa = f(a); fb = f(b); x1 = a; x0 = b;
if(fa * fb > 0)
t = "<font color=red><b>Funkcja nie spelnia zalozen</b></font>";
else
{
while(Math.abs(x1 - x0) > EPSX)
{
x1 = x0;
x0 = a - fa * (b - a) / (fb - fa);
f0 = f(x0);
if(Math.abs(f0) < EPS0) break;
if(fa * f0 < 0)
{
b = x0; fb = f0;
}
else
{
a = x0; fa = f0;
}
}
t += x0;
}
}
document.getElementById("out").innerHTML = t;
}
</script>
</div>
</body>
</html> |
Dokument ten rozpowszechniany jest zgodnie z zasadami licencji
GNU Free Documentation License. document.frmadminemail.adminemail_tytul.value = parent.document.title + " : " + document.title;
Źródło: mgr Jerzy Wałaszek



R
R
f(a) ; fb
f(b); x1
a; xo
b
fb > 0, pisz "Funkcja nie spełnia założeń" i zakończ algorytm
xo
fo < 0, to b
xo; fb
fo , inaczej a
xo; fa
fo