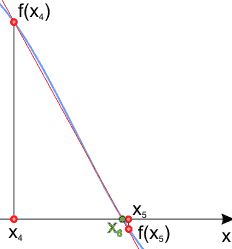
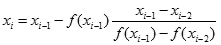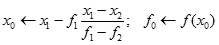Mamy daną funkcję f(x), dwa punkty startowe x1 oraz x2 i przedział <a,b> poszukiwań pierwiastka, do którego należą punkty x1, x2. W przedziale poszukiwań pierwiastka funkcja musi spełniać następujące warunki:
- Funkcja f(x) jest określona - dla każdej wartości argumentu x z przedziału <a,b> potrafimy policzyć wartość funkcji.
- Funkcja f(x) jest ciągła - jej wartości nie "wykonują" nagłych skoków. Funkcja przebiega przez wszystkie wartości pośrednie - nie istnieją zatem przerwy w kolejnych wartościach funkcji.
- Funkcja f(x) na krańcach przedziału <a,b> przyjmuje różne znaki (nie obowiązuje to punktów x1 i x2). Ponieważ funkcja, zgodnie z poprzednim wymogiem, jest ciągła, to przyjmuje w przedziale <a,b> wszystkie wartości pośrednie pomiędzy f(a) i f(b). Wartości te mają różne znaki (czyli leżą po różnych stronach osi OX), zatem musi być taki punkt xo w przedziale <a,b>, dla którego funkcja przyjmuje wartość pośrednią:
f(a) < f(xo) = 0 < f(b) lub f(a) > f(xo) = 0 > f(b)
- Dodatkowo w przedziale <a,b> pierwsza pochodna f '(x) jest różna od zera. Nie istnieje zatem minimum lub maksimum lokalne. Ten warunek gwarantuje nam, iż sieczna nie będzie równoległa do osi OX, co uniemożliwiłoby wyznaczenie jej punktu przecięcia z tą osią.
Gdy funkcja f(x) spełnia podane warunki, to w przedziale <a,b> istnieje pierwiastek i możemy go wyszukać metodą siecznych.
Metoda siecznych (ang. secant method) jest ulepszeniem metody regula falsi. W metodzie regula falsi żądamy, aby funkcja f(x) zawsze przyjmowała różne znaki na krańcach przedziału poszukiwań pierwiastka. Różne znaki gwarantują nam istnienie pierwiastka w tym przedziale. Otóż w metodzie siecznych taki wymóg nie jest konieczny (za wyjątkiem pierwszego obiegu). Do wyznaczenia kolejnego przybliżenia pierwiastka funkcji wykorzystujemy dwa poprzednio wyznaczone punkty:
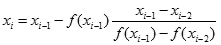
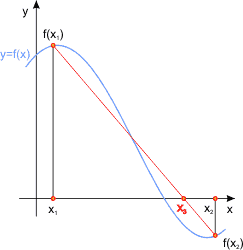
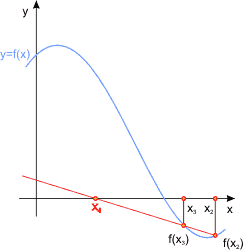
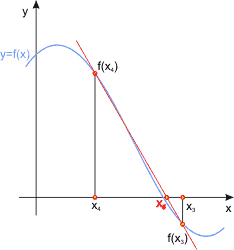
Okazuje się, iż takie podejście do problemu znacznie przyspiesza znajdowanie pierwiastka funkcji. Prześledźmy graficznie tok postępowania:
Jeśli punkty początkowe x1, x2 zostaną źle dobrane, to algorytm może nie dać rozwiązania. Dlatego stosujemy w nim dodatkowy licznik obiegów pętli wyznaczającej kolejne przybliżenia pierwiastka funkcji. Jeśli po wykonaniu zadanej liczby obiegów (u nas 64) nie zostanie znalezione rozwiązanie, to algorytm przerywa obliczenia z odpowiednim komunikatem. Obliczenia również będą przerwane w przypadku, gdy algorytm stwierdzi, iż sieczna jest równoległa do osi OX. Poprawnym warunkiem zakończenia algorytmu jest:
| xi-1 - xi-2 | < εx lub | f(xi) | < εo

Dane wejściowe
| f(x) | - | funkcja rzeczywista, której pierwiastek liczymy. Musi być ciągła i określona w przedziale poszukiwań pierwiastka. |
| x1, x2 | - | punkty krańcowe przedziału poszukiwań pierwiastka funkcji f(x). W dalszej fazie obliczeń punkty te przechowują dwie poprzednie wartości xo - x1 ostatnią, a x2 przedostatnią. x1, x2  R R |
Dane wyjściowe
| xo | - | pierwiastek funkcji f(x). xo  R R |
Zmienne pomocnicze i funkcje
| fo, f1 , f2 | - wartości funkcji odpowiednio w punktach x1, x2, xo. fo, f1 , f2  R R |
| i | - licznik obiegów pętli. Obiegi są zliczane wstecz od wartości i = 64. i  C C |
| εo | - określa dokładność porównania z zerem. εo = 0.0000000001 |
| εx | - określa dokładność wyznaczania pierwiastka xo. εx = 0.0000000001 |

| | krok 1: | Odczytaj x1 i x2 |
| | krok 2: | f1 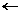 f(x1); f2 f(x1); f2 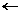 f(x2); i f(x2); i 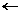 64 64 |
| | krok 3: | Dopóki i > 0 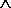 | x1 - x2 | > εx: wykonuj kroki 4..8 | x1 - x2 | > εx: wykonuj kroki 4..8 |
| krok 4: | Jeśli | f1 - f2 | < εo, pisz "Złe punkty startowe" i zakończ algorytm |
| krok 5: | 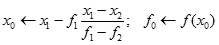 |
| krok 6: | Jeśli | fo | < εo, to idź do kroku 10 |
| krok 7: | x2 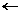 x1; f2 x1; f2 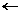 f1; x1 f1; x1 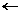 xo; f1 xo; f1 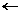 fo fo |
| krok 8: | i  i - 1 i - 1 |
| | krok 9: | Jeśli i = 0, pisz "Przekroczony limit obiegów" i zakończ algorytm |
| | krok 10: | Pisz xo i zakończ algorytm |

Wykonanie algorytmu siecznych rozpoczynamy od odczytu dwóch punktów x1 oraz x2. Punkty te posłużą do wyznaczenia pierwszej siecznej. Nie muszą one obejmować przedziału, w którym funkcja zmienia znak, jednakże jest to wskazane.
Dla obu punktów obliczamy wartości funkcji umieszczając je w zmiennych odpowiednio f1 i f2. Ponieważ algorytm siecznych może nie dać rozwiązania, stosujemy proste zabezpieczenie w postaci zliczania wykonanych obiegów pętli. Zmienna i pełni rolę licznika tych obiegów. Obiegi zliczane są wstecz. Na początku w zmiennej i określamy maksymalną ilość obiegów, po których algorytm zaprzestanie wykonywać obliczenia pierwiastka.
Rozpoczynamy pętlę obliczającą kolejne przybliżenia pierwiastka funkcji. Pętla kończy się w jednym z trzech przypadków:
1. Licznik i osiąga zero - wypisujemy odpowiedni komunikat i kończymy algorytm - pierwiastek nie został znaleziony, a xo zawiera zwykle jakieś przypadkowe wartości. Jest to sygnał, iż początkowe punkty x1 i x2 były zbyt odległe od pierwiastka funkcji.
2. Ostatnie dwa pierwiastki przybliżone x1 i x2 różnią się od siebie o εx lub mniej - w takim przypadku xo jest przybliżonym pierwiastkiem. Wypisujemy xo i kończymy algorytm.
3. Moduł różnicy wartości funkcji f1 i f2 dla dwóch ostatnich pierwiastków x1 i x2 jest równy zero. Ponieważ różnica ta występuje w mianowniku ułamka we wzorze obliczającym nowy pierwiastek xo, musimy przerwać obliczenia. Wypisujemy odpowiedni komunikat i kończymy algorytm.
Na początku pętli wyznaczamy nowe przybliżenie pierwiastka xo oraz wartość funkcji w tym punkcie fo. Do wyznaczenia xo stosujemy wzór siecznych, który wykorzystuje dwa ostatnio wyliczone przybliżenia pierwiastka x1 i x2.
Jeśli fo jest dostatecznie bliskie zeru, to xo jest przybliżonym pierwiastkiem, wypisujemy xo i kończymy algorytm.
W przeciwnym razie przesuwamy x1 i xo odpowiednio do x2 i x1 wraz z wartościami funkcji w tych punktach i kontynuujemy pętlę. Przesunięcie wartości funkcji f1 i fo zwalnia nas od konieczności ich ponownego wyliczania.

 | | |
| | |
| | | 
Poniższe, przykładowe programy są praktyczną realizacją omawianego w tym rozdziale algorytmu. Zapewne można je napisać bardziej efektywnie. To już twoje zadanie. Dokładny opis stosowanych środowisk programowania znajdziesz we wstępie. Programy przed opublikowaniem w serwisie edukacyjnym zostały dokładnie przetestowane. Jeśli jednak znajdziesz jakąś usterkę (co zawsze może się zdarzyć), to prześlij o niej informację do autora. Pozwoli to ulepszyć nasze artykuły. Będziemy Ci za to wdzięczni. | |
| | | | |
Programy wyznaczają miejsce zerowe funkcji:
f(x) = x3(x + sin(x2 - 1) - 1) - 1
Pierwiastków należy poszukiwać w przedziałach <-1,0> i <1,2>.
| Wydruk z uruchomionego programu |
Obliczanie pierwiastka funkcji - metoda siecznych
f(x) = x^3*(x+sin(x^2-1)-1)-1
-------------------------------------------------
(C)2006 mgr Jerzy Wałaszek I LO w Tarnowie
Podaj dwa wstępne punkty x1 i x2:
x1 = 1
x2 = 2
-------------------------------------------------
WYNIK:
x0 = 1,18983299
-------------------------------------------------
Koniec. Naciśnij klawisz Enter... |
| Microsoft Visual Basic 2005 Express Edition |
Borland
Delphi 7.0
Personal
Edition | // Program znajduje miejsce zerowe funkcji f(x)
// za pomocą algorytmu siecznych
//---------------------------------------------
// (C)2006 mgr J.Wałaszek I LO w Tarnowie
program mzf1;
{$APPTYPE CONSOLE}
uses math;
const
EPS0 = 0.0000000001; // dokładność porównania z zerem
EPSX = 0.0000000001; // dokładność wyznaczenia pierwiastka
// Funkcja, której miejsce zerowe obliczamy
// f(x) = x^3*(x+sin(x^2-1)-1)-1
// <-1,0> i <1,2>
//-----------------------------------------
function f(x : real) : real;
begin
Result := x * x * x * (x + sin(x * x - 1) - 1) - 1;
end;
//-----------------------------------------------------
// Program główny
//-----------------------------------------------------
var
x0,x1,x2,f0,f1,f2 : real;
i : integer;
begin
writeln('Obliczanie pierwiastka funkcji - metoda siecznych');
writeln('f(x) = x^3*(x+sin(x^2-1)-1)-1');
writeln('-------------------------------------------------');
writeln('(C)2006 mgr Jerzy Walaszek I LO w Tarnowie');
writeln;
writeln('Podaj dwa wstepne punkty x1 i x2:');
writeln;
write('x1 = '); readln(x1);
write('x2 = '); readln(x2);
writeln;
writeln('-------------------------------------------------');
writeln('WYNIK:');
writeln;
f1 := f(x1); f2 := f(x2); i := 64;
while (i > 0) and (abs(x1 - x2) > EPSX) do
begin
if abs(f1 - f2) < EPS0 then
begin
writeln('Zle punkty startowe');
i := 0;
break;
end;
x0 := x1 - f1 * (x1 - x2) / (f1 - f2);
f0 := f(x0);
if abs(f0) < EPS0 then break;
x2 := x1; f2 := f1;
x1 := x0; f1 := f0;
dec(i);
if i = 0 then writeln('Przekroczony limit obiegow');
end;
if i > 0 then writeln('x0 = ',x0:15:8);
writeln;
writeln('-------------------------------------------------');
writeln('Koniec. Nacisnij klawisz Enter...');
readln;
end. |
Borland
C++ Builder
6.0
Personal
Edition | // Program znajduje miejsce zerowe funkcji f(x)
// za pomocą algorytmu siecznych
//---------------------------------------------
// (C)2006 mgr J.Wałaszek I LO w Tarnowie
#include <iostream>
#include <iomanip>
#include <math>
using namespace std;
const double EPS0 = 0.0000000001; // dokładność porównania z zerem
const double EPSX = 0.0000000001; // dokładność wyznaczenia pierwiastka
// Funkcja, której miejsce zerowe obliczamy
// f(x) = x^3*(x+sin(x^2-1)-1)-1
// <-1,0> i <1,2>
//-----------------------------------------
double f(double x)
{
return x * x * x * (x + sin(x * x - 1) - 1) - 1;
}
//-----------------------------------------------------
// Program główny
//-----------------------------------------------------
int main(int argc, char* argv[])
{
double x0,x1,x2,f0,f1,f2;
int i;
cout.precision(8); // 8 cyfr po przecinku
cout.setf(ios::fixed); // format stałoprzecinkowy
cout << "Obliczanie pierwiastka funkcji - metoda siecznych\n"
"f(x) = x^3*(x+sin(x^2-1)-1)-1\n"
"-------------------------------------------------\n"
"(C)2006 mgr Jerzy Walaszek I LO w Tarnowie\n\n"
"Podaj dwa wstepne punkty x1 i x2:\n\n";
cout << "x1 = "; cin >> x1;
cout << "x2 = "; cin >> x2;
cout << "\n-------------------------------------------------\n\n"
"WYNIK:\n\n";
f1 = f(x1); f2 = f(x2); i = 64;
while(i && (fabs(x1 - x2) > EPSX))
{
if(fabs(f1 - f2) < EPS0)
{
cout << "Zle punkty startowe\n";
i = 0;
break;
}
x0 = x1 - f1 * (x1 - x2) / (f1 - f2);
f0 = f(x0);
if(fabs(f0) < EPS0) break;
x2 = x1; f2 = f1;
x1 = x0; f1 = f0;
if(!(--i)) cout << "Przekroczony limit obiegow\n";
}
if(i) cout << "x0 = " << setw(15) << x0 << endl;
cout << "\n---------------------------------------------\n";
system("pause");
return 0;
} |
Microsoft
Visual
Basic 2005
Express
Edition | ' Program znajduje miejsce zerowe funkcji f(x)
' za pomocą algorytmu siecznych
'---------------------------------------------
' (C)2006 mgr J.Wałaszek I LO w Tarnowie
Module Module1
Const EPS0 = 0.0000000001 ' dokładność porównania z zerem
Const EPSX = 0.0000000001 ' dokładność wyznaczenia pierwiastka
' Funkcja, której miejsce zerowe obliczamy
' f(x) = x^3*(x+sin(x^2-1)-1)-1
' <-1,0> i <1,2>
'-----------------------------------------
Function f(ByVal x As Double) As Double
Return x * x * x * (x + Math.Sin(x * x - 1) - 1) - 1
End Function
'-----------------------------------------------------
' Program główny
'-----------------------------------------------------
Sub Main()
Dim x0, x1, x2, f0, f1, f2 As Double
Dim i As Integer
Console.WriteLine("Obliczanie pierwiastka funkcji - metoda siecznych")
Console.WriteLine("f(x) = x^3*(x+sin(x^2-1)-1)-1")
Console.WriteLine("-------------------------------------------------")
Console.WriteLine("(C)2006 mgr Jerzy Wałaszek I LO w Tarnowie")
Console.WriteLine()
Console.WriteLine("Podaj dwa wstępne punkty x1 i x2:")
Console.WriteLine()
Console.Write("x1 = ") : x1 = Val(Console.ReadLine)
Console.Write("x2 = ") : x2 = Val(Console.ReadLine)
Console.WriteLine()
Console.WriteLine("-------------------------------------------------")
Console.WriteLine()
Console.WriteLine("WYNIK:")
Console.WriteLine()
f1 = f(x1) : f2 = f(x2) : i = 64
While (i > 0) And (Math.Abs(x1 - x2) > EPSX)
If Math.Abs(f1 - f2) < EPS0 Then
Console.WriteLine("Złe punkty startowe")
i = 0
Exit While
End If
x0 = x1 - f1 * (x1 - x2) / (f1 - f2)
f0 = f(x0)
If Math.Abs(f0) < EPS0 Then Exit While
x2 = x1 : f2 = f1
x1 = x0 : f1 = f0
i -= 1
If i = 0 Then Console.WriteLine("Przekroczony limit obiegów")
End While
If i > 0 Then Console.WriteLine("x0 = {0,15:F8}", x0)
Console.WriteLine()
Console.WriteLine("-------------------------------------------------")
Console.WriteLine("Koniec. Naciśnij klawisz Enter...")
Console.ReadLine()
End Sub
End Module |
| Python | # -*- coding: cp1250 -*-
# Program znajduje miejsce zerowe funkcji f(x)
# za pomocą algorytmu siecznych
#---------------------------------------------
# (C)2006 mgr J.Wałaszek I LO w Tarnowie
import math
EPS0 = 0.0000000001 # dokładność porównania z zerem
EPSX = 0.0000000001 # dokładność wyznaczenia pierwiastka
# Funkcja, której miejsce zerowe obliczamy
# f(x) = x^3*(x+sin(x^2-1)-1)-1
# <-1,0> i <1,2>
#-----------------------------------------
def f(x):
return x * x * x * (x + math.sin(x * x - 1) - 1) - 1
#-----------------------------------------------------
# Program główny
#-----------------------------------------------------
print "Obliczanie pierwiastka funkcji - metoda siecznych"
print "f(x) = x^3*(x+sin(x^2-1)-1)-1"
print "-------------------------------------------------"
print "(C)2006 mgr Jerzy Walaszek I LO w Tarnowie"
print
print "Podaj dwa wstepne punkty x1 i x2:"
print
x1 = float(raw_input("x1 = "))
x2 = float(raw_input("x2 = "))
print
print "--------------------------------------------------"
print
print "WYNIK:"
print
f1 = f(x1); f2 = f(x2); i = 64
while (i > 0) and (abs(x1 - x2) > EPSX):
if abs(f1 - f2) < EPS0:
print "Zle punkty startowe"
i = 0
break
x0 = x1 - f1 * (x1 - x2) / (f1 - f2)
f0 = f(x0)
if abs(f0) < EPS0: break
x2, f2 = x1, f1
x1, f1 = x0, f0
i -= 1
if i == 0: print "Przekroczony limit obiegow"
if i > 0: print "x0 = %15.8f" % x0
print
print "--------------------------------------------------"
raw_input("Koniec. Nacisnij klawisz Enter...") |
| JavaScript | <html>
<head>
</head>
<body>
<div align="center">
<form style="BORDER-RIGHT: #ff9933 1px outset; PADDING-RIGHT: 4px;
BORDER-TOP: #ff9933 1px outset; PADDING-LEFT: 4px;
PADDING-BOTTOM: 1px; BORDER-LEFT: #ff9933 1px outset;
PADDING-TOP: 1px; BORDER-BOTTOM: #ff9933 1px outset;
BACKGROUND-COLOR: #ffcc66" name="frmbincode">
<h3 style="TEXT-ALIGN: center">
Obliczanie pierwiastka funkcji metodą siecznych
</h3>
<p style="TEXT-ALIGN: center">
<i>f(x) = x<sup>3</sup>(x + sin(x<sup>2</sup> - 1) - 1) - 1</i>
</p>
<p style="text-align: center">
(C)2006 mgr Jerzy Wałaszek I LO w Tarnowie
</p>
<hr>
<p style="text-align: center">
Wpisz do pól edycyjnych dwa punkty dla pierwszej siecznej
</p>
<div align="center">
<table border="0" cellpadding="8" style="border-collapse: collapse">
<tr>
<td>
x<sub>1</sub> = <input type="text" name="wsp_x1" size="20"
value="1" style="text-align: right">
</td>
<td>
x<sub>2</sub> = <input type="text" name="wsp_x2" size="20"
value="2" style="text-align: right">
</td>
<td>
<input type="button" value="Szukaj pierwiastka" name="B1"
onclick="main()">
</td>
</tr>
</table>
</div>
<div id="out" align=center>...</div>
</form>
<script language=javascript>
// Program znajduje miejsce zerowe funkcji f(x)
// za pomocą algorytmu siecznych
//---------------------------------------------
// (C)2006 mgr J.Wałaszek I LO w Tarnowie
var EPS0 = 0.0000000001; // dokładność porównania z zerem
var EPSX = 0.0000000001; // dokładność wyznaczenia pierwiastka
// Funkcja, której miejsce zerowe obliczamy
// f(x) = x^3*(x+sin(x^2-1)-1)-1
// <-1,0> i <1,2>
//-----------------------------------------
function f(x)
{
return x * x * x * (x + Math.sin(x * x - 1) - 1) - 1;
}
//-----------------------------------------------------
// Program główny
//-----------------------------------------------------
function main()
{
var x0,x1,x2,f0,f1,f2,i,t;
x1 = parseFloat(document.frmbincode.wsp_x1.value);
x2 = parseFloat(document.frmbincode.wsp_x2.value);
if(isNaN(x1) || isNaN(x2))
t = "<font color=red><b>Nieprawidłowe dane!</b></font>";
else
{
f1 = f(x1); f2 = f(x2); i = 64;
while(i && (Math.abs(x1 - x2) > EPSX))
{
if(Math.abs(f1 - f2) < EPS0)
{
t = "<font color=red><b>Złe punkty startowe!</b></font>";
i = 0;
break;
}
x0 = x1 - f1 * (x1 - x2) / (f1 - f2);
f0 = f(x0);
if(Math.abs(f0) < EPS0) break;
x2 = x1; f2 = f1;
x1 = x0; f1 = f0;
if(!(--i))
t = "<font color=red><b>Przekroczony limit obiegów!</b></font>";
}
if(i) t = "x0 = " + x0;
}
document.getElementById("out").innerHTML = t;
}
</script>
</div>
</body>
</html> |
Dokument ten rozpowszechniany jest zgodnie z zasadami licencji
GNU Free Documentation License. document.frmadminemail.adminemail_tytul.value = parent.document.title + " : " + document.title;
Źródło: mgr Jerzy Wałaszek
R
R
R
C
f(x1); f2
f(x2); i
64
| x1 - x2 | > εx: wykonuj kroki 4..8
x1; f2
f1; x1
xo; f1
fo
i - 1