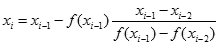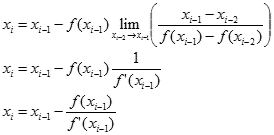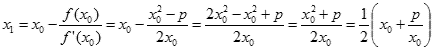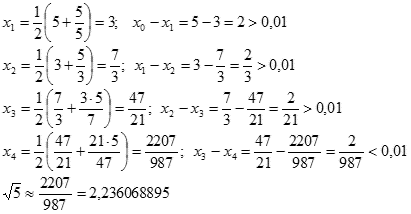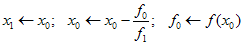Mamy daną funkcję f(x), jeden punkty startowy xo i przedział <a,b> poszukiwań pierwiastka, do którego należy punkt xo. W przedziale poszukiwań pierwiastka funkcja musi spełniać następujące warunki:
- Funkcja f(x) jest określona.
- Funkcja f(x) jest ciągła.
- Funkcja f(x) na krańcach przedziału <a,b> przyjmuje różne znaki.
- W przedziale <a,b> pierwsza pochodna f '(x) jest różna od zera.
Gdy funkcja f(x) spełnia podane warunki, to w przedziale <a,b> istnieje pierwiastek i możemy go wyszukać metodą Newtona. Jeśli we wzorze metody siecznych:
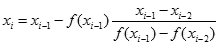
punkty xi-1 i xi-2 zaczną się do siebie zbliżać dążąc w granicy do równości, to ułamek tam występujący przejdzie w odwrotność pochodnej funkcji f(x) w punkcie xi-1:
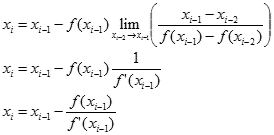
Sieczna w granicy stanie się styczną. Otrzymany wzór nosi nazwę wzoru Newtona. Pozwala on wyliczyć punkt przecięcia stycznej do wykresu funkcji w punkcie xi-1 z osią OX. Do wyznaczenia kolejnego przybliżenia pierwiastka xi potrzebujemy tylko jednego punktu, który został wyznaczony w poprzednim obiegu - w metodzie siecznych potrzebne były dwa punkty.
Zaletą metody Newtona jest bardzo szybka zbieżność. Wadą - we wzorze występuje pochodna, której obliczenie może być trudne dla niektórych funkcji. Jednakże metodę Newtona najczęściej stosuje się do wielomianów, których pochodne są bardzo proste i liczy się je algorytmicznie.
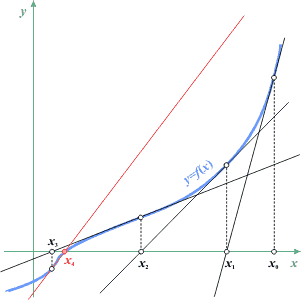
Zasada metody Newtona jest następująca:
Obliczenia rozpoczynamy od punktu xo leżącego dostatecznie blisko poszukiwanego pierwiastka funkcji. W przedziale pomiędzy punktem xo a docelowym pierwiastkiem funkcja musi posiadać niezerową pierwszą pochodną. Pożądane jest również, aby w punkcie xo druga pochodna miała ten sam znak, co funkcja f(x). W przeciwnym razie metoda Newtona zamiast zbliżać się do punktu pierwiastka ucieknie od niego.
Obliczamy nowy punkt xo zgodnie ze wzorem i sprawdzamy, czy wartość funkcji w tym punkcie jest dostatecznie bliska 0. Jeśli tak, kończymy. W przeciwnym razie wyznaczony kolejny punkt xo wykorzystując ostatnio wyliczony. Działania te prowadzimy dotąd, aż zbliżymy się dostatecznie do pierwiastka funkcji - różnica pomiędzy dwoma kolejno wyznaczonymi pierwiastkami będzie dostatecznie mała.
Ponieważ metoda Newtona może być rozbieżna przy źle wybranym punkcie startowym, będziemy zliczali obiegi - jeśli rozwiązanie nie pojawi się po wykonaniu zadanej ich liczby, przerwiemy obliczenia.

Znanym przykładem zastosowania metody Newtona jest rekurencyjne wyliczanie pierwiastka kwadratowego z danej liczby p. Wartość pierwiastka jest miejscem zerowym funkcji:
f(x) = x2 - p
Pochodna tej funkcji jest bardzo prosta i wyraża się wzorem:
f '(x) = 2x
Przyjmijmy za punkt startowy pewną liczbę x0. Wtedy pierwsze przybliżenie otrzymamy wg wzoru:
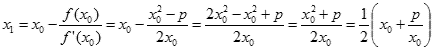
Kolejne przybliżenie otrzymamy podstawiając we wzorze za x0 otrzymane x1. Wg tej metody postępujemy dotąd, aż różnica dwóch ostatnich przybliżeń będzie mniejsza od pożądanej dokładności wyznaczenia pierwiastka. Dla przykładu wyznaczmy tą metodą pierwiastek z liczby 5 z dokładnością do 0,01. Za punkt początkowy przyjmijmy 5.
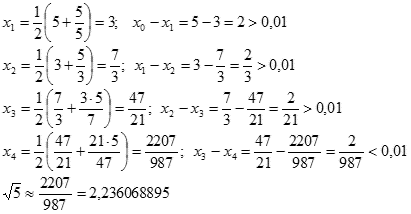
Sprawdźmy: 2,2360688952 = 5,000004103. Przybliżenie jest zatem bardzo dobre!

Dane wejściowe
| f(x) | - | funkcja, której pierwiastek liczymy. Musi być ciągła i określona w przedziale poszukiwań pierwiastka. |
| fp(x) | - | pierwsza pochodna funkcji f(x). W przedziale poszukiwań pierwiastka nie może przyjmować wartości 0. |
| xo | - | punkt startowy, od którego rozpoczynamy obliczenia pierwiastka funkcji f(x). xo  R R |
Dane wyjściowe
| xo | - | pierwiastek funkcji f(x) |
Zmienne pomocnicze i funkcje
| x1 | - poprzednie przybliżenie pierwiastka funkcji f(x). x1  R R |
| fo | - wartość funkcji w punkcie xo. fo  R R |
| f1 | - wartości pierwszej pochodnej funkcji punkcie xo. f1  R R |
| εo | - określa dokładność porównania z zerem. εo = 0.0000000001 |
| εx | - określa dokładność wyznaczania pierwiastka xo. εx = 0.0000000001 |

| | krok 1: | Odczytaj xo |
| | krok 2: | x1 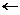 xo - 1; fo xo - 1; fo 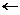 f(xo); i f(xo); i 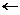 64 64 |
| | krok 3: | Dopóki i > 0 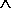 | x1 - xo | > εx | x1 - xo | > εx 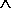 | fo | > εo: wykonuj kroki 4...7 | fo | > εo: wykonuj kroki 4...7 |
| krok 4: | f1 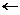 fp(xo) fp(xo) |
| krok 5: | Jeśli | f1 | < εo, pisz "Zły punkt startowy" i zakończ algorytm |
| krok 6: | 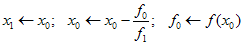 |
| krok 7: | i 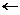 i - 1 i - 1 |
| | krok 8: | Jeśli i = 0, pisz "Przekroczony limit obiegów" i zakończ algorytm |
| | krok 9: | Pisz xo i zakończ algorytm |

Algorytm wyznaczania pierwiastka funkcji metodą Newtona rozpoczyna się od odczytu punktu startowego xo. W następnym kroku ustalamy wartość punktu x1 - będzie on przechowywał poprzednie przybliżenie pierwiastka. Jednakże na początku "poprzednie" przybliżenie jeszcze nie zostało policzone, zatem zmiennej x1 nadajemy taką wartość, aby wykonała się pętla wyliczająca pierwiastek funkcji. Dodatkowo do zmiennej fo wpisujemy wartość funkcji w punkcie xo oraz ustalamy maksymalną liczbę obiegów pętli na 64 w zmiennej i.
Rozpoczynamy pętlę wyliczającą kolejne przybliżenia pierwiastka. Pętla jest przerywana w następujących przypadkach:
1. Licznik i osiągnął 0. Oznacza to, iż algorytm nie wyznaczył pierwiastka w zadanej liczbie obiegów. Ponieważ metoda Newtona jest bardzo szybko zbieżna, to sytuacja taka może wystąpić tylko wtedy, gdy pomiędzy punktem startowym, a pierwiastkiem pierwsza pochodna zeruje się (styczna staje się równoległa do osi OX). W tej sytuacji algorytm wypisuje odpowiedni komunikat i kończy pracę.
2. Kolejne dwa przybliżenia różnią się o mniej niż εx. Kończymy algorytm wypisując wyznaczone w poprzednim obiegi xo.
3. Jeśli wyznaczona w poprzednim obiegu wartość funkcji w punkcie xo jest równa zero z dokładnością do εo. Kończymy algorytm wypisując xo.
Jeśli nie zajdzie żadna z opisanych powyżej trzech sytuacji, Wyznaczamy wartość pierwszej pochodnej w punkcie xo i umieszczamy wynik w zmiennej f1. Następnie sprawdzamy, czy wyliczona pochodna jest równa zero. Jeśli tak, musimy zakończyć algorytm z odpowiednim komunikatem, ponieważ we wzorze na przybliżony pierwiastek f1 występuje w mianowniku ułamka. Sytuacja taka może pojawić się przy źle dobranym punkcie startowym xo.
Przesuwamy xo do x1 zapamiętując w ten sposób poprzednio wyznaczony pierwiastek przybliżony funkcji. Obliczamy nowe przybliżenie pierwiastka i umieszczamy wynik w zmiennej xo. Wyznaczamy wartość funkcji w punkcie xo i umieszczamy wynik w zmiennej fo. Na końcu pętli zmniejszamy licznik i wykonujemy kolejny obieg.

 | | |
| | |
| | | 
Poniższe, przykładowe programy są praktyczną realizacją omawianego w tym rozdziale algorytmu. Zapewne można je napisać bardziej efektywnie. To już twoje zadanie. Dokładny opis stosowanych środowisk programowania znajdziesz we wstępie. Programy przed opublikowaniem w serwisie edukacyjnym zostały dokładnie przetestowane. Jeśli jednak znajdziesz jakąś usterkę (co zawsze może się zdarzyć), to prześlij o niej informację do autora. Pozwoli to ulepszyć nasze artykuły. Będziemy Ci za to wdzięczni. | |
| | | | |
Programy wyznaczają miejsce zerowe funkcji:
f(x) = x3(x + sin(x2 - 1) - 1) - 1
Pierwiastków należy poszukiwać w przedziałach <-1,0> i <1,2>.
| Wydruk z uruchomionego programu |
Obliczanie pierwiastka funkcji - metoda Newtona
f(x) = x^3*(x+sin(x^2-1)-1)-1
-----------------------------------------------
(C)2006 mgr Jerzy Wałaszek I LO w Tarnowie
Podaj punkt startowy x0 = 1
-----------------------------------------------
WYNIK:
x0 = 1,18983299
-----------------------------------------------
Koniec. Naciśnij klawisz Enter... |
| Microsoft Visual Basic 2005 Express Edition |
Borland
Delphi 7.0
Personal
Edition | // Program znajduje miejsce zerowe funkcji f(x)
// za pomocą algorytmu Newtona
//---------------------------------------------
// (C)2006 mgr J.Wałaszek I LO w Tarnowie
program mzf1;
{$APPTYPE CONSOLE}
uses math;
const
EPS0 = 0.0000000001; // dokładność porównania z zerem
EPSX = 0.0000000001; // dokładność wyznaczenia pierwiastka
// Funkcja, której miejsce zerowe obliczamy
// f(x) = x^3*(x+sin(x^2-1)-1)-1
// <-1,0> i <1,2>
//-----------------------------------------
function f(x : real) : real;
begin
Result := x * x * x * (x + sin(x * x - 1) - 1) - 1;
end;
// Oblicza pochodną funkcji f(x)
// f'(x) =2x^4*COS(x^2 - 1) + 3x^2*SIN(x^2 - 1) + 4x^3 - 3x^2
//-----------------------------------------------------------
function fp(x : real) : real;
begin
Result := x * x * (2 * x * x * cos(x * x - 1) + 3 * sin(x * x - 1) + 4 * x - 3)
end;
//-----------------------------------------------------
// Program główny
//-----------------------------------------------------
var
x0,x1,f0,f1 : real;
i : integer;
begin
writeln('Obliczanie pierwiastka funkcji - metoda Newtona');
writeln('f(x) = x^3*(x+sin(x^2-1)-1)-1');
writeln('-----------------------------------------------');
writeln('(C)2006 mgr Jerzy Walaszek I LO w Tarnowie');
writeln;
write('Podaj punkt startowy x0 = '); readln(x0);
writeln;
writeln('-----------------------------------------------');
writeln('WYNIK:');
writeln;
x1 := x0 - 1; f0 := f(x0); i := 64;
while (i > 0) and (abs(x1 - x0) > EPSX) and (abs(f0) > EPS0) do
begin
f1 := fp(x0);
if abs(f1) < EPS0 then
begin
writeln('Zly punkt startowy');
i := 0;
break;
end;
x1 := x0;
x0 := x0 - f0 / f1;
f0 := f(x0);
dec(i);
if i = 0 then writeln('Przekroczony limit obiegow');
end;
if i > 0 then writeln('x0 = ',x0:15:8);
writeln;
writeln('-----------------------------------------------');
writeln('Koniec. Nacisnij klawisz Enter...');
readln;
end. |
Borland
C++ Builder
6.0
Personal
Edition | // Program znajduje miejsce zerowe funkcji f(x)
// za pomocą algorytmu Newtona
//---------------------------------------------
// (C)2006 mgr J.Wałaszek I LO w Tarnowie
#include <iostream>
#include <iomanip>
#include <math>
using namespace std;
const double EPS0 = 0.0000000001; // dokładność porównania z zerem
const double EPSX = 0.0000000001; // dokładność wyznaczenia pierwiastka
// Funkcja, której miejsce zerowe obliczamy
// f(x) = x^3*(x+sin(x^2-1)-1)-1
// <-1,0> i <1,2>
//-----------------------------------------
double f(double x)
{
return x * x * x * (x + sin(x * x - 1) - 1) - 1;
}
// Oblicza pochodną funkcji f(x)
// f'(x) =2x^4*COS(x^2 - 1) + 3x^2*SIN(x^2 - 1) + 4x^3 - 3x^2
//-----------------------------------------------------------
double fp(double x)
{
return x * x * (2 * x * x * cos(x * x - 1) + 3 * sin(x * x - 1) + 4 * x - 3);
}
//-----------------------------------------------------
// Program główny
//-----------------------------------------------------
int main(int argc, char* argv[])
{
double x0,x1,f0,f1;
int i;
cout.precision(8); // 8 cyfr po przecinku
cout.setf(ios::fixed); // format stałoprzecinkowy
cout << "Obliczanie pierwiastka funkcji - metoda Newtona\n"
"f(x) = x^3*(x+sin(x^2-1)-1)-1\n"
"-----------------------------------------------\n"
"(C)2006 mgr Jerzy Walaszek I LO w Tarnowie\n\n"
"Podaj punkt startowy x0 = ";
cin >> x0;
cout << "\n-----------------------------------------------\n\n"
"WYNIK:\n\n";
x1 = x0 - 1; f0 = f(x0); i = 64;
while (i && (fabs(x1 - x0) > EPSX) && (fabs(f0) > EPS0))
{
f1 = fp(x0);
if(fabs(f1) < EPS0)
{
cout << "Zly punkt startowy\n";
i = 0;
break;
}
x1 = x0;
x0 = x0 - f0 / f1;
f0 = f(x0);
if(!(--i)) cout << "Przekroczony limit obiegow\n";
}
if(i) cout << "x0 = " << setw(15) << x0 << endl;
cout << "\n-------------------------------------------\n";
system("pause");
return 0;
} |
Microsoft
Visual
Basic 2005
Express
Edition | ' Program znajduje miejsce zerowe funkcji f(x)
' za pomocą algorytmu Newtona
'---------------------------------------------
' (C)2006 mgr J.Wałaszek I LO w Tarnowie
Module Module1
Const EPS0 = 0.0000000001 ' dokładność porównania z zerem
Const EPSX = 0.0000000001 ' dokładność wyznaczenia pierwiastka
' Funkcja, której miejsce zerowe obliczamy
' f(x) = x^3*(x+sin(x^2-1)-1)-1
' <-1,0> i <1,2>
'-----------------------------------------
Function f(ByVal x As Double) As Double
Return x * x * x * (x + Math.Sin(x * x - 1) - 1) - 1
End Function
' Oblicza pochodną funkcji f(x)
' f'(x) =2x^4*COS(x^2 - 1) + 3x^2*SIN(x^2 - 1) + 4x^3 - 3x^2
'-----------------------------------------------------------
Function fp(ByVal x As Double) As Double
Return x * x * (2 * x * x * Math.Cos(x * x - 1) + _
3 * Math.Sin(x * x - 1) + 4 * x - 3)
End Function
'-----------------------------------------------------
' Program główny
'-----------------------------------------------------
Sub Main()
Dim x0, x1, f0, f1 As Double
Dim i As Integer
Console.WriteLine("Obliczanie pierwiastka funkcji - metoda Newtona")
Console.WriteLine("f(x) = x^3*(x+sin(x^2-1)-1)-1")
Console.WriteLine("-----------------------------------------------")
Console.WriteLine("(C)2006 mgr Jerzy Wałaszek I LO w Tarnowie")
Console.WriteLine()
Console.Write("Podaj punkt startowy x0 = ") : x0 = Val(Console.ReadLine)
Console.WriteLine()
Console.WriteLine("-----------------------------------------------")
Console.WriteLine()
Console.WriteLine("WYNIK:")
Console.WriteLine()
x1 = x0 - 1 : f0 = f(x0) : i = 64
While (i > 0) And (Math.Abs(x1 - x0) > EPSX) And (Math.Abs(f0) > EPS0)
f1 = fp(x0)
If Math.Abs(f1) < EPS0 Then
Console.WriteLine("Zły punkt startowy")
i = 0
Exit While
End If
x1 = x0
x0 = x0 - f0 / f1
f0 = f(x0)
i -= 1
If i = 0 Then Console.WriteLine("Przekroczony limit obiegów")
End While
If i > 0 Then Console.WriteLine("x0 = {0,15:F8}", x0)
Console.WriteLine()
Console.WriteLine("-----------------------------------------------")
Console.WriteLine("Koniec. Naciśnij klawisz Enter...")
Console.ReadLine()
End Sub
End Module |
| Python | # -*- coding: cp1250 -*-
# Program znajduje miejsce zerowe funkcji f(x)
# za pomocą algorytmu Newtona
#---------------------------------------------
# (C)2006 mgr J.Wałaszek I LO w Tarnowie
import math
EPS0 = 0.0000000001 # dokładność porównania z zerem
EPSX = 0.0000000001 # dokładność wyznaczenia pierwiastka
# Funkcja, której miejsce zerowe obliczamy
# f(x) = x^3*(x+sin(x^2-1)-1)-1
# <-1,0> i <1,2>
#-----------------------------------------
def f(x):
return x * x * x * (x + math.sin(x * x - 1) - 1) - 1
# Oblicza pochodną funkcji f(x)
# f'(x) =2x^4*COS(x^2 - 1) + 3x^2*SIN(x^2 - 1) + 4x^3 - 3x^2
#-----------------------------------------------------------
def fp(x):
return x*x*(2*x*x*math.cos(x*x - 1) + 3*math.sin(x*x - 1) + 4*x - 3)
#-----------------------------------------------------
# Program główny
#-----------------------------------------------------
print "Obliczanie pierwiastka funkcji - metoda Newtona"
print "f(x) = x^3*(x+sin(x^2-1)-1)-1"
print "-----------------------------------------------"
print "(C)2006 mgr Jerzy Walaszek I LO w Tarnowie"
print
x0 = float(raw_input("Podaj punkt startowy x0 = "))
print
print "---------------------------------------------------"
print
print "WYNIK:"
print
x1, f0, i = x0 - 1, f(x0), 64
while (i > 0) and (abs(x1 - x0) > EPSX) and (abs(f0) > EPS0):
f1 = fp(x0)
if abs(f1) < EPS0:
print "Zly punkt startowy"
i = 0
break
x1 = x0
x0 = x0 - f0 / f1
f0 = f(x0)
i -= 1
if i == 0: print "Przekroczony limit obiegow"
if i > 0: print "x0 = %15.8f" % x0
print
print "---------------------------------------------------"
raw_input("Koniec. Nacisnij klawisz Enter...") |
| JavaScript | <html>
<head>
</head>
<body>
<form style="BORDER-RIGHT: #ff9933 1px outset; PADDING-RIGHT: 4px;
BORDER-TOP: #ff9933 1px outset; PADDING-LEFT: 4px;
PADDING-BOTTOM: 1px; BORDER-LEFT: #ff9933 1px outset;
PADDING-TOP: 1px; BORDER-BOTTOM: #ff9933 1px outset;
BACKGROUND-COLOR: #ffcc66" name="frmbincode">
<h3 style="TEXT-ALIGN: center">
Obliczanie pierwiastka funkcji metodą Newtona
</h3>
<p style="TEXT-ALIGN: center">
<i>f(x) = x<sup>3</sup>(x + sin(x<sup>2</sup> - 1) - 1) - 1</i>
</p>
<p style="TEXT-ALIGN: center">
(C)2006 mgr Jerzy Wałaszek I LO w Tarnowie
</p>
<hr>
<p style="text-align: center">
Wpisz do pola edycyjnego punkt startowy
</p>
<div align="center">
<table border="0" id="table144" cellpadding="8"
style="border-collapse: collapse">
<tr>
<td>
x<sub>0</sub> = <input type="text" name="wsp_x0" size="20"
value="1" style="text-align: right">
</td>
<td>
<input type="button" value="Szukaj pierwiastka" name="B1"
onclick="main()">
</td>
</tr>
</table>
</div>
<div id="out" align=center>...</div>
</form>
<script language=javascript>
// Program znajduje miejsce zerowe funkcji f(x)
// za pomocą algorytmu Newtona
//---------------------------------------------
// (C)2006 mgr J.Wałaszek I LO w Tarnowie
var EPS0 = 0.0000000001; // dokładność porównania z zerem
var EPSX = 0.0000000001; // dokładność wyznaczenia pierwiastka
// Funkcja, której miejsce zerowe obliczamy
// f(x) = x^3*(x+sin(x^2-1)-1)-1
// <-1,0> i <1,2>
//-----------------------------------------
function f(x)
{
return x * x * x * (x + Math.sin(x * x - 1) - 1) - 1;
}
// Oblicza pochodną funkcji f(x)
// f'(x) =2x^4*COS(x^2 - 1) + 3x^2*SIN(x^2 - 1) + 4x^3 - 3x^2
//-----------------------------------------------------------
function fp(x)
{
return x * x * (2 * x * x * Math.cos(x * x - 1) +
3 * Math.sin(x * x - 1) + 4 * x - 3);
}
//-----------------------------------------------------
// Program główny
//-----------------------------------------------------
function main()
{
var x0,x1,f0,f1,i,t;
x0 = parseFloat(document.frmbincode.wsp_x0.value);
if(isNaN(x0))
t = "<font color=red><b>Błędne dane wejściowe</b></font>";
else
{
x1 = x0 - 1; f0 = f(x0); i = 64;
while (i && (Math.abs(x1 - x0) > EPSX) && (Math.abs(f0) > EPS0))
{
f1 = fp(x0);
if(Math.abs(f1) < EPS0)
{
t = "<font color=red><b>Zly punkt startowy</b></font>";
i = 0;
break;
}
x1 = x0;
x0 = x0 - f0 / f1;
f0 = f(x0);
if(!(--i)) t = "<font color=red><b>Przekroczony limit obiegow</b></font>";
}
if(i) t = "x<sub>0</sub> = " + x0;
}
document.getElementById("out").innerHTML = t;
}
</script>
</div>
</body>
</html>
Dokument ten rozpowszechniany jest zgodnie z zasadami licencji
GNU Free Documentation License.
document.frmadminemail.adminemail_tytul.value = parent.document.title + " : " + document.tit
|
Źródło: mgr Jerzy Wałaszek

![]()
R
R
R
R
xo - 1; fo
f(xo); i
64
| x1 - xo | > εx
| fo | > εo: wykonuj kroki 4...7
fp(xo)
i - 1