Ułożenie dowolnej magicznej kostki - w tym kostki Rubika - nie musi być skomplikowane. Należy tylko poznać algorytm.
Wstęp
Tematem tej części mojej witryny są łamigłówki logiczne: kostka Rubika i jej większe odpowiedniki. Przedstawiono tu sprawy dość banalne, za to interesujące każdego miłośnika tych łamigłówek – przede wszystkim metodę układania, tj. przywracania kostek do stanu uporządkowanego. Choć w internecie można znaleźć wiele miejsc, gdzie tematyka ta jest omówiona szczegółowo (zob. linki), w opisie tutaj zamieszczonym zaprezentowano elementy dotąd prawdopodobnie nigdzie niepublikowane.

Kostki, zarówno oryginalna (o rozmiarze 3×3×3, autor: Ernő Rubik), jak i jej większe odpowiedniki: „zemsta Rubika” (4×4×4, autor: Péter Sebestény) oraz „kostka profesorska” (5×5×5, autor: Udo Krell), są doskonałymi zabawkami, zarówno dla dzieci, jak i dla dorosłych, i stanowią idealną alternatywę dla komputera czy wideo. Uczą wytrwałości, spostrzegawczości, zręczności, zapamiętywania ruchów, ćwiczą koncentrację, wyobraźnię przestrzenną, stanowią także świetny trening dla mięśni palców. Istnieją zawody w układaniu kostki Rubika na czas, jednak tego typu „sport” ma swoich zwolenników i przeciwników wśród miłośników kostek. Kostką zainteresowali się także matematycy, widząc w niej świetny model dla pewnych zagadnień z dziedziny kombinatoryki i teorii grup. Tutaj nie będą jednak omawiane ani kwestie matematyczne, ani tematyka układania na czas.

Kostka Rubika i jej młodsze i większe siostry to łamigłówki dość skomplikowane. Sposób ich układania dla wielu ludzi stanowi rodzaj wiedzy tajemnej. Nie zmienia tego wcale fakt, że liczne strony i publikacje prezentują potrzebne do tego opisujące algorytmy w sposób zdawałoby się bardzo poglądowy, z użyciem graficznych przedstawień lub wręcz animacji potrzebnych ruchów. Wydaje się jednak, że nie w poglądowości rzecz. Na tej witrynie zostanie zaprezentowana inna metoda, która może okazać się odpowiedniejsza dla niektórych adeptów sztuki kręcenia kostką. Nic jednak nie zastąpi osobistej chęci, zainteresowanie, a także gotowości poświęcenia czasu. Oczywiście niezbędne jest też zdobycie samej kostki (lub kostek).

Dziś kostki względnie łatwo można kupić w sklepach z zabawkami, także w sklepach internetowych. Z uwagi na dość skomplikowaną budowę nie są to niestety wyroby tanie („kostka profesorska” kosztuje obecnie – tj. na początku 2007 roku – około 135 zł, „zemsta Rubika” jest niemal o połowę tańsza, kostka Rubika kosztuje z kolei mniej więcej połowy ceny „zemsty”). Czasami można znaleźć na rynku tańsze kostki, które są jednak mało trwałe.
Warto w tym miejscu przestrzec wszystkich, że większe kostki mają sporo ruchomych części i dlatego nie za bardzo nadają się do układania na czas. Przy zwykłej zabawie także nie należy używać zbyt wielkiej siły, która mogłaby grozić zniszczeniem dość drogich przedmiotów rozrywki. Kostkę, która przy kręceniu stawia duży opór, można przesmarować, upychając specjalny smar do kostek w szczelinach między elementami. Dobrze w tej roli spisuje się także krem Nivea. Kostkę Rubika można również rozebrać na części i nasmarować mechanizm wewnętrzny.
Uwaga: nie każdy układ ruchomych elementów, z których składają się opisywane tutaj łamigłówki, da się uzyskać przy pomocy kręcenia ścianami, wychodząc ze stanu uporządkowanego. Dlatego jeżeli kostka z jakiegoś powodu rozpadnie się na części, należy zawsze składając ją odtworzyć uporządkowany, pierwotny układ elementów. Innymi słowy: źle złożonej kostki nie da się ułożyć. Powinni o tym pamiętać wszyscy chcący oskarżać o oszustwo kolegów, którzy jak twierdzą posiedli umiejętność układania tej interesującej łamigłówki, a nie mogą sobie poradzić z dostarczonym im egzemplarzem.
Zapraszam do lektury i kręcenia kostką!
Uwaga. Źródłem grafiki na tej stronie jest częściowo Wikipedia (duże fotografie), częściowo schematy wykonane przeze mnie według wzorów znalezionych w Sieci. Cała grafika udostępniona jest każdemu do swobodnego kopiowania i modyfikowania, na licencji GNU obowiązującej w Wikipedii.
Podstawy
Na początku lat 80-tych ubiegłego wieku nasz kraj opanowała kostkomania. Pojawiła się wówczas w sklepach oryginalna kostka Rubika, reklamowana jako układanka niemalże niemożliwa do samodzielnego rozpracowania. Ludzie (zwłaszcza młodzi, ale nie tylko) kupowali ją masowo pomimo dość wygórowanej ceny (początkowo sprzedawano wyłącznie węgierskie oryginały), a nauczyciele matematyki w liceach dawali uczniom oceny bardzo dobre za samodzielne rozszyfrowanie niektórych elementów sposobu układania kostki. Jak niosła wówczas wieść gminna, pewni studenci rozpracowali do końca algorytm układania łamigłówki i pocztą pantoflową rozeszły się „wzory na kostkę”. Być może ta poczta nie działała wówczas dostatecznie sprawnie i ograniczyła się tylko do pewnych środowisk i rejonów kraju, a być może ówczesne metody popadły dziś w zapomnienie, faktem jest jednak, że w istniejących dziś publikacjach w ogóle nie wspomina się tamtego systemu. Aby uchronić od zapomnienia osiągnięcia ówczesnej młodzieży, zdecydowałem napisać i opublikować na mojej witrynie zestaw stron poświęconych układaniu kostki, z uwzględnieniem tamtych metod właśnie. Warto dodać, że tą metodą (opracowaną przez anonimowych twórców i jedynie propagowaną przeze mnie) nauczyło się układać kostkę wielu ludzi także w czasach zupełnie nam nieodległych.

Zacznijmy jednak od rzeczy najprostszych. Weźmy do ręki kostkę Rubika (tę o rozmiarze 3×3×3) i przyjrzyjmy się jej dokładnie. Jak widać, ma ona kształt sześcianu o ścianach podzielonych na 9 elementów (wyglądających jak mniejsze kostki), które można przemieszczać względem siebie w odpowiedni sposób – poprzez obracanie ścianami. Ułożenie kostki jest możliwe dzięki odpowiedniej metodzie (dzięki odpowiedniemu algorytmowi), która polega na zastosowaniu określonych obrotów określonych ścian w określonej kolejności. Istnieje wiele metod układania kostki. Każda metoda składa się z kilku etapów (jakie to etapy, dowiemy się w dalszej części), które stanowią jakby fazy realizacji złożonego przedsięwzięcia. Na każdym z etapów mamy do wykonania określone zadanie, które możemy zrealizować dzięki odpowiedniej procedurze polegającej na wykonaniu określonej sekwencji ruchów (obrotów). Sekwencje te określamy także jako procesy, manewry, kombinacje, a nawet wzory.
Wśród elementarnych kostek składających się na naszą łamigłówkę możemy wyróżnić 3 rodzaje elementów:
- 6 środków ścian,
- 12 kantów („krawężników”), które należą jednocześnie do dwóch ścian i są pomalowane na 2 kolory,
- 8 narożników („rogów”), które należą jednocześnie do trzech ścian i są pomalowane na 3 kolory.
Uwaga: Oto jest zestaw terminów, które należy dobrze przyswoić, aby w ogóle rozumieć treść publikowanych tu wyjaśnień. I tak, słowo ściana odnosi się zawsze do kostki jako całości; kostka ma sześć ścian. Umówmy się ponadto, że ścianka jest terminem odnoszącym się do elementu kostki – środka, kantu lub narożnika. A zatem na jednej ścianie widać 9 ścianek, z których każdy należy do innego elementu. Środek ma tylko jedną ściankę i znajduje się pośrodku ściany. Kanty znajdują się na krawędziach kostki i mają po dwie ścianki, należące do dwóch sąsiadujących ścian. Narożniki znajdują się w wierzchołkach kostki i mają po trzy ścianki, z których każda należy do jednej z trzech ścian, które schodzą się w danym wierzchołku.
Oryginalna kostka Rubika ma ustalony układ kolorów, a na białym środku znajduje się logo firmy. Jeśli odwrócimy kostkę ścianą białą do góry, a ściana zielona będzie skierowana w prawo, wówczas prosto w naszą stronę skierowana będzie ściana pomarańczowa, pod spodem znajdzie się ściana żółta, w lewo skierowana będzie ściana niebieska, wreszcie z tyłu kostki znajdzie się (zasłonięta przed naszym wzrokiem) ściana czerwona (właściwie ciemnoczerwona, prawie brązowa). Kostki o innym schemacie malowania są podróbkami (co nie znaczy, że nie da się ich ułożyć korzystając z zamieszczonych tu informacji).
Kolor ściany znaczy tyle, co kolor środka. Środki można obracać (wraz z całą ścianą), lecz nie można ich przemieszczać względem innych środków. Oznacza to na przykład, że jeśli trzymamy oryginalną, nieułożoną kostkę żółtym środkiem do góry, a czerwonym skierowanym w naszą stronę, to zawsze po prawej odnajdziemy środek zielony, po lewej niebieski, z tyłu pomarańczowy i u dołu biały. Ustawienia środków nie da się zmienić nawet rozbierając kostkę i składając ją z powrotem w przypadkowy sposób (czego, jak już mówiliśmy, robić nie można, bo kostki przypadkowo złożonej może nie dać się ułożyć). Dzieje się tak dlatego, że wewnątrz kostki znajduje się specjalny krzyż, a na końcu jego ramion znajdują się właśnie środki ścian.
Ktoś, kto wziął kostkę pierwszy raz do ręki (i nie zdążył pomieszać jej ułożenia), może oczywiście próbować samodzielnie analizować, jakie skutki przynosi wykonanie określonej kombinacji ruchów, jest jednak mało prawdopodobne, aby doszedł tym sposobem do konstruktywnych wniosków (i samodzielnie opracował algorytm układania kostki). Dlatego wszystkim początkującym kostkowiczom doradzam, aby nie bali się pobawić swoją zabawką. Popróbujcie trochę nią pokręcić, za chwilę będę miał dla was zadanie do wykonania i trochę obycia z kostką przyda wam się jak znalazł…
w internecie spotkać można różne sposoby przedstawiania manewrów kostki – od czysto tekstowych do animacji. Amatorzy kostki opracowali system schematycznego zapisywania obrotów kostki przy pomocy liter. Wydawnictwa polskojęzyczne promują nasz polski standard, warto jednak także poznać zapis angielski, dzięki któremu uzyskamy dostęp do licznych źródeł kostkarskiej wiedzy.
Zapis przykładowej sekwencji w systemie polskim może wyglądać tak: C2G'P'LC2PL'G'C2. Zapis tej samej sekwencji w systemie angielskim przedstawia się natomiast tak: F2U'R'LF2RL'U'F2. Litera jest skrótem nazwy ściany:
| system polski | system angielski | ||
|---|---|---|---|
| T | tylna | B | back |
| L | lewa | L | left |
| G | górna | U | up |
| P | prawa | R | right |
| C | czołowa | F | front |
| D | dolna | D | down |
Apostrof po literze oznacza obrót w lewo, tj. przeciwnie do ruchu wskazówek zegara. Dwójka oznacza natomiast obrót o 180° (czyli obrót dwukrotny). Kierunek obrotu określamy zawsze tak, jakbyśmy patrzyli na daną ścianę, dlatego obrót prawą ścianą do siebie jest obrotem w lewo, zaś obrót lewą ścianą do siebie jest obrotem w prawo (sprawdź na swojej kostce!). Na razie jednak nie należy się tym wszystkim zbytnio przejmować.
Uwaga: zaprezentowany system oznaczeń jest najczęstszy, choć nie jest jedynym używanym. Na jednej z witryn internetowych wprowadzono na przykład zapisy ze znakami + i -, które jednak niekoniecznie oznaczają obroty w lewo i prawo, ponadto litera B oznacza tam bottom, czyli ścianę dolną. Dlatego jeśli chcemy skorzystać z literatury, zapoznajmy się najpierw szczegółowo ze stosowanym systemem.
Symboliczna metoda zapisu ruchów jest być może dobra (zwłaszcza jeśli już dobrze zna się znaczenie użytych symboli), ciekawe jednak, ile przeciętnie czasu potrzeba, aby zapamiętać sekwencję znaków (liter, dwójek, apostrofów) nietworzących żadnego sensownego wyrazu. Jeszcze lepszą metodą prezentacji ruchów są niewątpliwie rysunki i animacje, ułatwiające ułożenie kostki, jednak znów pojawia się problem, jak te wszystkie ruchy zapamiętać. Być może są ludzie, mający pamięć wzrokową pozwalającą na zapamiętanie animacji klatka po klatce, jednak zdecydowana większość będzie miała z tym duże kłopoty. A przecież nie jest sztuką pochwalić się znajomym, że umiemy ułożyć kostkę, by następnie gdy trzeba będzie udowodnić swoje umiejętności wyciągnąć kartkę z tajemniczymi rysunkami i z jej pomocą zabrać się do dzieła. Pamiętajmy, że prawdziwy kostkomaniak potrafi ułożyć kostkę bez pomocy kartek czy monitora komputera.
Moim zadaniem nie jest więc jedynie pokazać zainteresowanym, jak ułożyć kostkę – chodzi raczej o to, aby nauczyć początkujących tej sztuki, i to tak, aby w przyszłości mogli to robić sami. Przedstawiona tu metoda nie jest więc ani szczególnie elegancka, ani szczególnie szybka, ani nawet szczególnie często pokazywana w internecie, jest za to najbardziej prosta ze znanych mi metod, wymaga zapamiętania minimalnej ilości sekwencji, a ponadto sekwencje te łatwo zapamiętać.
Zastanówmy się, jakie długie sekwencje przychodzi nam zapamiętywać w życiu codziennym. Otóż są to często różnego rodzaju liczby, a właściwie sekwencje cyfr: telefony, daty urodzin, numery NIP, PIN itd. Właśnie dlatego dla początkującego kostkomaniaka najlepsze nie są metody oparte na zapamiętaniu liter ani tym bardziej prezentacje animacji ruchów kostki, ale właśnie nieco bardziej abstrakcyjne, ale o wiele łatwiejsze w zapamiętaniu metody oparte na cyfrach. Tak przynajmniej pokazuje doświadczenie w przeważającej ilości przypadków.
Zanim jednak dojdziemy do sedna, spróbujmy trochę pobawić się naszą kostką. Ostatecznie Rubik wymyślił ją jako pomoc dydaktyczną do kształcenia wyobraźni przestrzennej (i do ćwiczenia pamięci). Poćwiczmy trochę bez niczyjej pomocy, i spróbujmy samodzielnie ułożyć jedną ścianę (dowolnego koloru). Zapewniam, że jest to możliwe, i przy pewnej dozie cierpliwości dość łatwe do osiągnięcia. W czasach kostkowego szaleństwa radził sobie z tym zadaniem praktycznie każdy, i nie ma powodu, by przypuszczać, że dziś ludzie są głupsi niż ćwierć wieku temu (może jedynie mniej cierpliwi…). W kolejnych częściach zostanie podane rozwiązanie wszystkich możliwych problemów tego wstępnego etapu, jednak jest wskazane, by mimo to spróbować samemu.
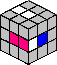
Od razu jednak wyjaśnijmy sobie jedną rzecz, zwłaszcza, że w internecie można znaleźć kursy układania kostki, których autorzy świadomie bądź nieświadomie stosują dezinformację i wprowadzają czytelnika w błąd. Otóż ścianę uważamy za ułożoną tylko wtedy, gdy wszystkie 9 budujących ją elementów znajduje się we właściwym miejscu. Nie wystarczy, że na zewnątrz prezentuje się jeden kolor na tych elementach, jak na rysunku (kolor szarych ścianek jest nieistotny):

Wbrew temu, co wypisują owi „nauczyciele”, nie ma najmniejszego sensu, aby zaczynać od „ułożenia” ściany, jeśli kanty i narożniki od samego początku nie będą zajmować swoich miejsc. A zatem na przykład kant czerwono-żółty musi znajdować się na granicy ściany czerwonej i tej o żółtym środku, a nie gdziekolwiek indziej na czerwonej ścianie, inaczej nasze układanie nie przyniesie dokładnie niczego. Kostka taka jak na powyższym rysunku jest wciąż zupełnie nieułożona, a metody porządkowania owej rzekomo ułożonej ściany są bardziej skomplikowane niż jej rzeczywiste układanie od podstaw.
Innymi słowy, ściana jest ułożona dopiero wtedy, gdy boczne ścianki budujących ją klocków tworzą wraz ze środkami sąsiednich ścian rodzaj litery T, jak na rysunku:

Dopóki nie nauczysz się osiągać takiego właśnie efektu, nie opowiadaj znajomym, że potrafisz ułożyć ścianę kostki Rubika, bo nie będzie to prawdą. Przede wszystkim uwierz, że potrafisz, i zacznij od ułożenia krzyża, to znaczy najpierw umieść na swoich miejscach kanty, jak na rysunku poniżej (oczywiście tym razem układamy ścianę zieloną, a nie żółtą jak na rysunku poprzednim!):

Dopiero potem zajmij się układaniem narożników.
Tymczasem życzę ci miłego kręcenia i szybkiego osiągnięcia biegłości w samodzielnym układaniu jednej ściany, bez pomocy żadnych wzorów i sekwencji. Gdy uznasz, że umiejętność tę opanowałeś (lub też, czego nie życzę, że nie jesteś w stanie opanować), zapraszam do kolejnej części. Porównanie własnych umiejętności z przedstawionymi propozycjami przyniesie zapewne pozytywne rezultaty.
Kurs układania kostki 3×3×3 dla początkujących
Jak już wspomniano wyżej, istnieje dużo rożnych metod układania kostki Rubika. Wbrew temu, co często sądzą ludzie, którzy z kostką nie mieli styczności, w żadnej metodzie nie układa się kolejno sześciu ścian kostki – byłoby to po prostu bardzo niepraktyczne. Zaprezentowany poniżej sposób układania kostki należy do grupy metod określanych jako „warstwa po warstwie”. Inną szeroko stosowaną grupą jest „najpierw narożniki”. Mało znane i trudniejsze metody to „najpierw kanty” i różnego typu metody mieszane.
Nauka układania kostki podzielona jest na etapy. Dany etap ćwiczymy tak długo (wychodząc od nieułożonej kostki), aż poczujemy się pewnie i nie będziemy musieli korzystać z notatek, stron internetowych itp. Naturalnie ćwicząc np. etap 3 musimy każdorazowo powtarzać także etapy 1 i 2.
W pierwszych dwóch etapach będziemy układać jedną ścianę kostki. W części poprzedniej zaleciłem jako ćwiczenie układanie dowolnej ze ścian. Układanie ścian różnych kolorów jest dobrym ćwiczeniem dla wyobraźni przestrzennej i orientacji na kostce, ale przeszkadza w układaniu całej kostki. W tym celu należy raczej zdecydować się na układanie jednej konkretnej ściany, stale tego samego koloru.
Warto może przypomnieć, że środki ścian mają niezmienne położenie i determinują kolor ściany. Ściana biała jest to zatem ta ściana, której środek jest biały. Na schematach przedstawiono układanie właśnie ściany białej, w rzeczywistości może być to dowolny inny kolor. Jeżeli układana kostka nie jest oryginalna i ma układ kolorów inny niż standardowy, dobrze jest układać najpierw ścianę przeciwległą do ściany żółtej. Ściana żółta układana będzie bowiem jako trzecia i najtrudniejsza warstwa, i rozmieszczenie żółtego koloru na schematach może mieć kluczowe znaczenie.
Etap pierwszy
Celem pierwszego etapu jest ułożenie krzyża z kantów na jednej ze ścian. Narożniki nie interesują nas na razie zupełnie.
Ściana, którą będziemy teraz układać, będzie stanowić późniejszy fundament układanej warstwami kostki. Gdy trzymamy kostkę w rękach, nie widzimy zwykle ściany dolnej, i dlatego układanie kostki na podobieństwo budowania domu, tj. kierując budowaną ścianę w dół, jest niezbyt wygodnie i odradzane. A zatem na razie obróćmy całą kostkę tak, by środek układanej ściany (białej) był skierowany w górę (jak pamiętamy, środki nie zmieniają położenia względem siebie). Jeżeli układana kostka nie ma oryginalnego układu kolorów, można poćwiczyć układanie ściany białej, aby po osiągnięciu tej umiejętności już bez pomocy opisów i schematów ułożyć ścianę przeciwległą do żółtej.
W czasie tego etapu możemy obracać kostką wedle bieżących potrzeb, jednak tak, aby ku górze stale była skierowana biała ściana. Możemy zatem kręcić całą kostką jak globusem, nie wolno nam jej jednak wywracać do góry nogami ani kłaść na boku.
Spójrzmy najpierw, czy na białej ścianie nie ma już przypadkiem właściwie zorientowanych kantów, tj. obróconych białą częścią do góry. Jeśli jest taki kant, obróćmy górną ścianę tak, aby boczna ścianka tego kantu sąsiadowała ze środkiem ściany odpowiedniego koloru. Przykład pokazano na rysunkach:
|
|
|
Schematy przedstawiają kolejne fazy wykonywania manewru, należy je zawsze czytać od lewej do prawej. Widać na nich jedynie ścianę górną (tutaj: biała), czołową (niebieska) i prawą (pomarańczowa). Na rysunkach nie ma strzałek informujących, którą ścianą należy kręcić i w którą stronę, gdyż naprawdę nie jest to potrzebne dla osoby posiadającej minimum wyobraźni przestrzennej i obycia z kostką. Jeśli ktoś jednak nie potrafi powtórzyć zilustrowanej operacji na swojej kostce, niech poszuka w linkach stron z animacjami. Przypominam też, że kolorem szarym oznaczono kolory nieistotne. Kostka ma uczyć między innymi koncentracji uwagi, musimy więc umieć skupić się tylko na zaznaczonych, kolorowych elementach i całkowicie zapomnieć o pozostałych.
Zgodnie z zapowiedzią, nie musimy się na razie niczego uczyć na pamięć, jednak opisany w poprzedniej części system oznaczeń warto przy okazji poznawać sukcesywnie. A zatem, zobrazowany powyżej proces można zapisać jako G' w wersji polskiej, U' w angielskiej.
Wróćmy do układania krzyża z kantów na białej ścianie. Może się zdarzyć, że znajdują się tam już białe kanty, lecz są niewłaściwie zorientowane:
|
|
Mogą też być właściwie zorientowane, lecz nie da się tak ustawić białej ściany, aby oba były na właściwych miejscach:
|
|
W takich przypadkach należy przede wszystkim sprawdzić, czy na ścianie dolnej bezpośrednio pod wadliwie ustawionym kantem nie znajduje się inny kant biały. Jeżeli jest taki, należy obrócić dolną ścianą, aby bez pośrednio pod wadliwym kantem nie było kantu białego. Następnie należy wykonać dwukrotny obrót ścianą boczną zawierającą wadliwy kant tak, aby znalazł się on na ścianie dolnej.
A oto jak ustawić oba kanty z ostatniego schematu na właściwe pozycje:
|
|
 |
|
|
|
| 1 | 2 | 3 | 4 | 5 |
Zapis manewru w wersji polskiej: P2D'G'C2, w wersji angielskiej: R2D'U'F2. Zapis ten wygląda okropnie i raczej nie nadaje się do wkucia na pamięć, a przecież sama operacja jest chyba dość prosta i logiczna (prześledź dokładnie drogę każdego z kantów). Co więcej, wiemy też, co zrobić, jeśli właściwy kant znajduje się na ścianie dolnej i jest zorientowany białym kolorem w dół – wystarczy wówczas ustawić go jak w położeniu 4 i wykonać dwukrotny obrót ścianą przednią (do położenia 5).
A jak rozwiązać sytuację, gdy kanty znajdują się co prawda na górnej ścianie. lecz są źle zorientowane? Oto poprawne rozwiązanie sytuacji poprzedniej (ściana zielona znajduje się naprzeciwko niebieskiej):
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | 5 |
Zapis manewru: pol. C'L'P'C', ang. F'L'R'F'. Sprawdź, że lewa ściana rzeczywiście kręci się w lewo (między poz. 2 a 3), tj. przeciwnie do ruchu wskazówek zegara.
Powyższy manewr pokazuje także, co zrobić w niektórych przypadkach, gdy biały kant znajduje się w warstwie środkowej. Przeanalizuj w tym celu pozycje 2 i 3, a następnie 4 i 5. W innych wypadkach ściągamy najpierw ów kant do warstwy dolnej, najlepiej tak, aby biała ścianka tego kantu znalazła się pod spodem. Wówczas przekręcamy dolną ścianę tak, aby kant znalazł się dokładnie pod swoim miejscem przeznaczenia i dalej wiemy już co robić (poz. 4 i 5 sekwencji poniżej).
Kostka Rubika nie jest przecież sejfem, ale układanką logiczną! Przy układaniu krzyża z kantów nie należy więc sugerować się ścisłymi wzorami, lecz własną wyobraźnią. Dwie kolejne sekwencje mogą pomóc tym, którzy są jej naprawdę pozbawieni i nie radzą sobie mimo dotychczasowych wskazówek.
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | 5 |
Zapis manewru: pol. P'D'PC2, ang. R'D'R'F2.
W pozycji 1 mamy nieciekawą sytuację na ścianie czołowej: biało-czerwony kant jest źle zorientowany i nie da się go umieścić na swoim miejscu prostym ruchem C' (czyli kręcąc ścianą czołową w lewo). Ściągamy go więc w dół (poz. 2) tak, by biała ścianka znalazła się na spodzie (zgodnie z zaleceniem). Wymaga to jednak obrotu ścianą prawą, na której mamy już ułożony kant biało-niebieski. Ruch ścianą dolną do pozycji 3 powoduje, że kant czerwono-biały opuszcza ścianę prawą i można już wrócić kantem biało-niebieskim do jego właściwego położenia (poz. 4). Ruch 2 – 3 ustawił nam kant biało-czerwony w wygodnej pozycji do wstawienia na miejsce, co dokonujemy ruchem C2 z poz. 4 do 5.
Tę samą sytuację wyjściową można też jednak rozwiązać inaczej.
|
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | 5 | 6 |
Zapis manewru: pol. CDPC'P', ang. FDRF'R'. Sekwencja poz. 2 – 3 – 4 – 5 pokazuje, jak należy poradzić sobie z sytuacją, gdy kant znajdujący się na dolnej ścianie jest skierowany w dół innym kolorem niż biały. Zauważmy wymuszony obrót w poz. 3 – 4 i powrót w poz. 5 – 6 wówczas, gdy nie przeszkadza to już w procesie ustawienia kantu biało-czerwonego.
Sztuka układania krzyża z kantów na jednej ścianie nie należy do skomplikowanych, należy ją jednak dobrze poćwiczyć przed przejściem do następnego etapu. Pamiętajmy też o dostatecznym wypoczynku.
Etap drugi
Celem drugiego etapu jest ułożenie jednej ze ścian do końca poprzez umieszczenie narożników na właściwych pozycjach. Kanty zostały ułożone w poprzednim etapie, musimy więc tak operować kostką, aby nie zniszczyć elementów już ułożonych. Na szczęście nie jest to takie trudne.
Uwaga: w niektórych metodach zaleca się, aby ułożyć tylko 3 narożniki i pozostawić jeden nieułożony do końca etapu kolejnego. W rzeczywistości nie jest to wcale potrzebne i w metodzie tu opisanej pierwszą ścianę układamy do końca.
Kostka ma tylko 8 narożników, z których połowę umieścimy na właściwych miejscach w trakcie tego etapu. Zaczynamy od narożników z białą ścianą znajdujących się w dolnej warstwie kostki (o ile takie są). Źle ułożone narożniki znajdujące się na układanej ścianie mogą bowiem zostać wypchnięte na dogodniejsze miejsce w czasie umieszczania we właściwej pozycji tych, które znajdują się na dole.
Przed przystąpieniem do operacji musimy odpowiednio zorientować kostkę i dolną ścianę:
- kostkę trzymamy układaną ścianą do góry tak, by docelowe miejsce dla układanego narożnika znajdowało się w wierzchołku utworzonym przez ściany górną, czołową i prawą,
- dolną ścianą kręcimy tak, aby narożnik przeznaczony do eksportu znalazł się pod miejscem docelowym, tj. w wierzchołku utworzonym przez ściany dolną, czołową i prawą.
Narożnik przeznaczony do wstawienia może przyjąć jedną z trzech orientacji, i w zależności od tego stosujemy odpowiednią metodę postępowania. Oczywiście nie uczymy się ruchów na pamięć, ale śledzimy drogę narożnika i staramy się zrozumieć jej przebieg i go zapamiętać.
Pierwsza orientacja:
|
|
|
|
|
| A1 | A2 | A3 | A4 |
| pol.: P'D'P | |||
| ang.: R'D'R | |||
Druga orientacja:
|
|
|
|
|
| B1 | B2 | B3 | B4 |
| pol.: CDC' | |||
| ang.: FDC' | |||
Trzecia orientacja:
|
|
|
|
|
|
|
| C1 | C2 | C3 | C4 | C5 | C6 |
| pol.: P'T'D2TP | |||||
| ang.: R'B'D2BP | |||||
Komentarza wymaga trzeci przypadek. Zwróćmy uwagę, że ruch C1 – C2 (obrót prawą ścianą) powoduje, że biała ścianka narożnika przestaje być skierowana w dół – narożnik przyjmuje taką orientację jak w A1. Jest jednak w innym miejscu, ponadto ściana prawa znajduje się już w „roboczym” takim jak w A2. Z kolei jednak w A2 inna jest pozycja układanego narożnika, należy więc zastosować pewien sprytny chwyt. Ruchem C2 – C3 (obrót ścianą tylną w lewo – przekonaj się, że naprawdę ściana ta kręci się przeciwnie do ruchu wskazówek zegara, jeśli spojrzeć prosto na nią) obracamy narożnik do takiej pozycji, jaką powinien zajmować w A2 – choć wciąż nie znajduje się on we właściwym miejscu. Obrót dolną ścianą o 180° (C3 – C4) rozwiązuje ten problem – narożnik jest gotowy do wstawienia na swoją pozycję, nie zapominajmy jednak o ścianie tylnej, którą wychyliliśmy. Zanim wstawimy narożnik na właściwe miejsce, musimy jeszcze cofnąć ten obrót tylnej ścianki ruchem C4 – C5. Końcowy obrót C5 – C6 jest już identyczny jak A3 – A4.
Jeśli nie ma żadnych białych narożników na dolnej ściance, a u góry wciąż pozostały narożniki nie na swoim miejscu lub w złej orientacji, musimy je wypchnąć umieszczając na ich miejscu dowolny narożnik z dołu. Korzystamy ze schematu A lub B (bo składają się z mniejszej liczby ruchów), najlepiej tak, by wypchnięty narożnik nie znalazł się białą ścianką do dołu, widzimy przecież, że ta pozycja jest najbardziej kłopotliwa. Tu nie podam żadnych rysunków i dalszych wskazówek. Jeśli wybierzemy zły schemat wypychając źle ułożony narożnik na dół, nie stanie się nic złego poza tym, że będziemy musieli zastosować dłuższą kombinację po to, by umieścić go na swoim miejscu. Nie ma obawy, że zniszczymy elementy juz ułożone (o ile nie popełnimy jakiegoś poważnego błędu), a zatem możemy eksperymentować śmiało. W końcu kostka Rubika jest układanką stworzoną dla rozrywki, a nie bomba unieszkodliwianą odpowiednim kodem. W rozrywce nie chodzi zaś o to, by dokładnie odtworzyć proponowaną tu procedurę. Jeśli uda nam się znaleźć alternatywny sposób wykonania jakiejś akcji (bez naruszenia już ułożonych części), możemy zawsze śmiało go zastosować i nic złego się nie stanie, ani kostce, ani nam.
Narożniki można umieszczać też na swoich miejscach w nieco inny sposób, stosując odrobinę dłuższe kombinacje, za to takie, które można wykorzystać także w innych sytuacjach, jak się okaże w etapie trzecim. Podane wyżej schematy A, B i C całkowicie wystarczają, jednak warto zapoznać się także z metodami alternatywnymi, choćby po to, by układanie kostki nam się szybko nie znudziło.
Pierwsza orientacja:
|
|
|
|
|
|
| a1 | a2 | a3 | a4 | a5 |
| pol.: DCD'C' | ||||
| ang.: DFD'F' | ||||
Druga orientacja:
|
|
|
|
|
|
| b1 | b2 | b3 | b4 | b5 |
| pol.: D'P'DP | ||||
| ang.: D'R'DR | ||||
Trzecia orientacja:
|
|
|
|
|
|
|
|
| c1 | c2 | c3 | c4 | c5 | c6 | c7 |
| pol.: CD'C'P'D2P | ||||||
| ang.: FD'F'R'D2R | ||||||
I znów objaśnienia odnośnie trzeciej orientacji. Układany narożnik w ruchu c2 – c3 jest przesuwany w jedyny dolny wierzchołek kostki, który nie ulegnie zmianie przy ruchu ścianą zarówno czołową, jak i prawą. Dzięki tej pozycji można bez problemów cofnąć ścianę czołową do swojego normalnego położenia (c3 – c4), jak i wychylić ścianę prawą (c4 – c5) na przyjęcie narożnika (c5 – c6).
Po dobrym opanowaniu sześciu przedstawionych manewrów nie jest chyba potrzebne podawanie kombinacji ruchów potrzebnych do obrotu narożnika znajdującego się we właściwym położeniu, ale o złej orientacji. Takie kombinacje istnieją i nawet będą nam potrzebne, ale na razie świetnie możemy się bez nich obyć i dlatego poćwiczmy tylko to, czego nauczyliśmy się dotąd.
Zauważmy, że jak dotąd nie było nam potrzebne uczenie się na pamięć żadnych kombinacji, a wszelkie zapisy były podawane nie w celu ich przyswojenia, ile raczej po to, by się z nimi oswoić. Manewry oznaczone jako A i B (a także a i b używane w ich zastępstwie) są chyba tak proste, że każdy może nauczyć się ich bez stosowania ściąg. Także manewr C (i c) nie wymaga w rzeczywistości uczenia się kombinacji, wystarczy jedynie uważnie obserwować, co dzieje się z układanym narożnikiem. Procesy alternatywne (a, b i c), choć dłuższe o jeden ruch, są chyba nawet bardziej intuicyjne niż procesy krótsze (A, B i C). Proponuję teraz je dobrze przećwiczyć, a dalszą częścią sposobu układania kostki zająć się po dłuższym wypoczynku.
Możemy się już także pochwalić znajomym, że umiemy ułożyć samodzielnie jedną ścianę kostki. Zapewniam, że jest to już niezłe osiągnięcie. Przeciętny człowiek potrzebuje sporo czasu, by dojść bez pomocy do zasad systematycznego użycia przedstawionych tu kombinacji ruchów, choć jest to w pełni wykonalne. Jeśli komuś udało się dojść do tego miejsca samodzielnie, bez mojej pomocy, serdecznie gratuluję.
Można też próbować ułożyć drugą warstwę kostki („drugi pasek”), oczywiście tak, by nie zniszczyć już ułożonej ściany. Choć nie jest to zadanie proste, jest na pewno wykonalne. Znam ludzi, którzy sami doszli do właściwego sposobu uważnie obserwując, co na etapie drugim dzieje się nie tylko z narożnikami, ale i z kantami. Czy i ty podejmiesz się tego wyzwania? Tak czy inaczej, zapraszam do zapoznania się z następną częścią kursu.
Etap trzeci
Celem trzeciego etapu jest ułożenie środkowej warstwy kostki poprzez umieszczenie 4 kantów na właściwych pozycjach. W poprzednich etapach udało nam się ułożyć całą ścianę, musimy więc tak operować kostką, aby nie zniszczyć elementów już ułożonych. Na szczęście nie jest to takie trudne, a z lektury tej witryny Czytelnik dowie się nawet o dwóch różnych sposobach rozwiązania problemu.
Do tej pory, jak pamiętamy, trzymaliśmy kostkę do góry nogami. Układaliśmy jej dolną warstwę, traktując ją jak górną ścianę. Teraz czas kostkę odwrócić do właściwego położenia. Od tej pory będziemy zatem trzymać kostkę tak, aby ku górze była skierowana ściana żółta. Oczywiście można wybrać dowolną inną ścianę, trudniej będzie jednak wówczas posługiwać się schematami.
Zaczynamy od wyszukania na górnej ścianie (tej dotąd nieułożonej) kantów, które nie mają żółtej ścianki. Przypuśćmy, że znaleźliśmy kant o ściankach niebieskiej i czerwonej, przy czym ścianka niebieska znajduje się na górze (sąsiaduje z żółtym środkiem ściany górnej).
I teraz przychodzi najtrudniejszy moment… Otóż musimy całą kostkę ułożyć tak, aby ściana koloru górnej ścianki kantu, który chcemy ustawić, znajdowała się na pozycji ścianki tylnej. Obróćmy następnie górną ścianę tak, aby układany kant znalazł się jak najbliżej nas, tj. na krawędzi ściany górnej i czołowej.
Spójrzmy na rysunek, na którym wyobrażono taką właśnie sytuację oglądaną od tyłu kostki. Wygląda to tak, jakby niebieska ścianka kantu „celowała” w kierunku niebieskiej ściany. Zwróćmy uwagę, że na rysunku widzimy ścianę tylną (niebieską), lewą (czerwoną) i górną (żółtą).

Zobaczmy teraz to samo od strony układającego i nieco z lewej. Tym razem widzimy ściankę lewą (czerwoną), czołową (zieloną) i górną (żółtą):

Tego typu zmiany ustawienia kamery śledzącej ruchy kostki są jak najbardziej celowe i na miejscu. Przypomnijmy sobie bowiem po raz kolejny, że kostka ma służyć do rozwoju wyobraźni przestrzennej. Stąd właśnie na przykład brak oznaczeń ścian na schematach: Czytelnik musi sam poćwiczyć wyobraźnię na tyle, aby dojść do tego, z której właściwie strony widać kostkę na danym schemacie. Jest to zresztą zawsze opisane w tekście.
A oto kolejne obroty potrzebne do umieszczenia naszego kantu we właściwej pozycji, widziane w taki sam sposób, jak kostka na poprzednim schemacie:
|
|
|
|
|
|
|
|
|
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 |
| pol.: T'GTGLG'L' | |||||||
| ang.: B'UBULU'L' | |||||||
Przedstawiony proces opiszemy też słownie. A zatem zauważamy, że układany kant ma kolor ściany tylnej (niebieski) i lewej (czerwony). Skoncentrujmy się na krawędzi docelowej naszego kantu, znajdującą się między ścianą tylną a lewą. W pierwszym ruchu zwanym ”krawędź w górę” (A1 – A2) sprawiamy, że krawędź ta zostaje umieszczona na ścianie górnej, przed układanym kantem, czyli staje się krawędzią ściany górnej i tylnej. Drugi ruch zwany „kolor do koloru” (A2 – A3) polega na tym, że obracamy ścianą górną tak, aby czerwona ścianka układanego kantu znalazła się bezpośrednio przy środku czerwonej ściany. Trzeci ruch to „krawędź wraca” (A3 – A4) – istotnie, cofamy ruch pierwszy. Czwarty ruch to „kręcimy dalej” (A4 – A5) – górna ścianka kręci się dalej w tym samym kierunku, co w ruchu drugim. Piąty ruch to „znów krawędź w górę” (A5 – A6) – tym razem jednak obraca się druga ze ścianek tworząca krawędź (ścianka lewa, a nie tylna jak poprzednio). Szósty ruch to „odkręcamy” (A6 – A7), gdyż cofamy obrót ściany górnej wykonany w ruchu czwartym. I wreszcie ruch siódmy to „znów krawędź wraca” (A7 – A8). Jego nazwa jest chyba zrozumiała.
Manewr umieszczania kantu w środkowej warstwie warto wykonywać, powtarzając (głośno lub w myślach) nazwy kolejnych ruchów. Tak naprawdę istotne jest tylko początkowe ustawienie kostki i ściany górnej, kierunek „wyciągania” krawędzi w pierwszym ruchu oraz poprawny obrót górnej ściany w ruchu „kolor do koloru”. Potem jeszcze trzeba zapamiętać, że tylna ściana musi wrócić na swoje miejsce, a reszta właściwie robi się sama. A zatem choć sekwencja składa się z 7 ruchów, nie ma potrzeby uczyć się jej na pamięć. Do tego cztery ostatnie ruchy powinny wydać nam się mocno znajome, o ile zainteresowaliśmy się alternatywnymi sposobami układania narożników w fazie drugiej.
Układanie kantu, który powinien znaleźć się między ścianą tylną a prawą wygląda bardzo podobnie. Jeśli nauczymy się podanych wyżej nazw ruchów, nie dostrzeżemy w ogóle żadnej różnicy. Na wszelki wypadek obejrzyjmy jednak schemat tego manewru. Tym razem będziemy układać kant zielono-czerwony, a przedstawione ścianki to czołowa (niebieska), prawa (czerwona) i górna (żółta).
|
|
|
|
|
|
|
|
|
| B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 |
| pol.: TG'T'G'P'GP | |||||||
| ang.: BU'B'U'R'UR | |||||||
Nieprzyjemny bywa przypadek, gdy udało się pozbyć wszystkich kantów bez żółtej ścianki z warstwy górnej, a mimo to nie cała druga warstwa jest ułożona. Źle ustawiony lub źle zorientowany kant należy wówczas wypchnąć na górę, wciskając na jego miejsce dowolny inny kant (byle wówczas nie pogubić się w schemacie ruchów, jako że kolory nie będą się przecież zgadzać), a gdy już znajdzie się on na ścianie górnej, wówczas będziemy już mogli umieścić go na swoim miejscu.
Na początku tego etapu wspomniałem, że istnieją dwa sposoby układania kantów drugiej warstwy. Drugi sposób można potraktować jako ciekawostkę, można też opanować go i stosować wymiennie z pierwszym jako urozmaicenie. Szczególnie przydatny okaże się on zwłaszcza posiadaczom kostek o rozmiarze większym, a więc zemsty Rubika i kostki profesorskiej.
W drugim sposobie wykorzystamy – dla prostoty przedstawienia – specjalne obroty, zwane ruchami sandwiczowymi lub po prostu kanapkowymi. Dotąd obracaliśmy jedynie ścianami kostki, tym razem zastosujemy obrót warstwy środkowej. Na przykład ruch sandwiczowy ściany prawej w lewo (zob. schemat poniżej) wykonujemy w ten sposób, że chwytamy prawą ręką nie tylko prawą ścianę, ale także warstwę środkową równoległą do prawej ściany, przekręcamy całość w żądanym kierunku, a następnie wracamy już samą ścianą prawą w poprzednie położenie. Zauważmy, że w wyniku ruchu sandwiczowego w istocie zmienia się położenie czterech środków ścian, odpowiadające obrotowi całej kostki wokół pewnej osi.
|
|
|
W notacji polskiej ruchy kanapkowe oznacza się poprzez dodanie indeksu k do litery oznaczającej daną ścianę. Opisany powyżej ruch oznaczymy więc jako Pk' (lub P'k). W notacji angielskiej ruchy sandwiczowe podaje się dodając literę M (od middle) przed literą oznaczającą daną ścianę. Można też użyć małej litery zamiast dużej. A zatem opisany ruch sandwiczowy notowany będzie jako MR' lub r'. Zauważmy przy okazji, że zapisy MR' i ML oznaczają dokładnie to samo – obrót sandwiczowy, który wykonywany jest w lewo patrząc od strony ściany prawej, jest jednocześnie obrotem w prawo patrząc od strony ściany lewej. To samo oznaczają również zapisy MF' i MB oraz MU' i MD.
Właściwie bez notacji ruchów sandwiczowych można by się obyć zupełnie (zilustrowany powyżej ruch można przecież przedstawić jako PL'), gdyby nie dwa fakty. Po pierwsze, upraszczają one często rozmaite formuły procesów dokonywanych na kostce. Po drugie, ruchy sandwiczowe i tak są konieczne przy kostkach o większych rozmiarach niż kostka Rubika.
Proces, który teraz przedstawię, można by śmiało nazwać Procesem Podstawowym (PP), gdyż różne jego odmiany mają podstawowe znaczenie przy układaniu kostek różnego rozmiaru. W przypadku układania kantów drugiej warstwy kostki musimy zacząć od takiego samego układu, jak w sposobie standardowym opisanym powyżej (układany kant „celuje” w ścianę o takim samym kolorze, jak jego górna ścianka). Będziemy układać podobnie jak poprzednio kant zielono-czerwony, a na schematach zobaczymy kostkę z nieco innej perspektywy – tak, aby uwidocznić ściany tylną (zieloną), prawą (czerwoną) i górną (żółtą).
|
|
|
|
|
|
|
|
|
| b1 | b2 | b3 | b4 | b5 | b6 | b7 | b8 |
| pol.: Pk'G'P'GPkG'P | |||||||
| ang.: MR'U'R'UMRU'R | |||||||
Zauważmy przede wszystkim, że ścianą górną obracamy na przemian – w lewo, w prawo, w lewo. W pierwszym ruchu b1 – b2 wykonujemy ruch sandwiczowy warstwą startową, tj. tą, w której znajduje się układany kant: ścianą górną staje się teraz ściana zielona, ścianą tylną – biała itd. Na ścianie tylnej pojawił się biały rząd, w tym kant biało-zielony, który musimy ochronić. W tym celu w ruchu drugim obrotem ściany górnej w lewo (b2 – b3) umieszczamy go w bezpiecznym miejscu z lewej strony ściany górnej. Teraz w ruchu trzecim obracamy warstwę docelową (tj. ścianą prawą) równolegle do obrotu warstwy startowej (b3 – b4). Kolejny, czwarty ruch górnej ściany przywraca na miejsce chroniony kant biało-zielony (b4 – b5) i jest odwrotnością ruchu drugiego; przy okazji ruch ten jednak zmienia położenie narożnika biało-zielono-czerwonego. W ruchu piątym odwracamy ruch pierwszy, wykonując obrót sandwiczowy (b5 – b6) i przywracając kolory ścian jak na początku układania. Zwróćmy uwagę, że do przemieszczonego narożnika dołączamy w ten sposób układany kant. Ruch szósty (b6 – b7) to kolejny obrót ściany górnej przywracający narożnik na swoje miejsce, a przy okazji umieszczający we właściwym położeniu na ścianie prawej układany kant. Wreszcie ruch siódmy (b7 – b8) cofa ruch trzeci i przywraca właściwe położenie warstwy docelowej (ściany prawej).
Bardzo łatwo posłużyć się podobnym procesem (a), gdy miejsce docelowe układanego kantu znajduje się na ścianie lewej. Ilustracje są chyba naprawdę niepotrzebne, pamiętajmy jedynie, że warstwą docelową będzie teraz ściana lewa, a ruch drugi musi umieszczać chroniony kant po stronie prawej. Podam tylko zapis procesu „a” w notacji polskiej: P'kGLG'PkGL' lub LkGLG'L'kGL' (jest to dokładnie to samo, jedynie inaczej oznaczone są ruchy sandwiczowe), oraz w notacji angielskiej: MR'ULU'MRUL lub MLULU'ML'UL'. Sprawdź koniecznie, czy potrafisz wykonać taki manewr bez korzystania ze schematów! Postaraj się posłużyć opisem słownym, a nie zapisem przy pomocy symboli.
Ostatecznie posługując się bądź procesami standardowymi (A, B), bądź też procesami z ruchami sandwiczowymi (a, b), udało się nam ułożyć dwie warstwy kostki. Jest to powód do zasłużonej dumy. Jak dotąd nie musieliśmy też uczyć się żadnych formułek na pamięć, a wszystkie manewry należało opanować śledząc ruchy odpowiednich kantów lub narożników. Przed nami jednak najtrudniejsza część: ułożenie warstwy górnej. Jak poprzednio, przed przystąpieniem do dalszej części zalecam dokładne przećwiczenie poznanych dotąd etapów i porządny wypoczynek, zwłaszcza że czeka nas sporo nowości.
Udało się nam ułożyć dwie warstwy kostki w trzech kolejnych etapach. Ułożenie trzeciej, ostatniej warstwy jest jednak znacznie trudniejsze i zostanie rozłożone aż na cztery etapy. Kolejność tych etapów bywa różna w różnych algorytmach typu „warstwa po warstwie”. Tutaj zostanie zaprezentowany algorytm składający się z następujących faz: właściwego zorientowania kantów, ułożenia kantów, ułożenia narożników i na koniec właściwego zorientowania narożników. Taka kolejność nie wydaje się zbyt elegancka, prowadzi za to najszybciej do celu i wymaga zapamiętania dokładnie jednej kombinacji ruchów na każdym etapie.
Trzeba w tym miejscu wyraźnie zaznaczyć, że przeciętnie uzdolniony człowiek jest w stanie samodzielnie ułożyć dwie warstwy kostki, próbując znaleźć rozwiązanie samodzielnie i dostatecznie długo. Niestety, nie każdy ma tyle wytrwałości i chęci, dlatego znakomita większość ludzi woli skorzystać z gotowych przepisów. Jednak znów, każdy człowiek, z którym się dotąd spotkałem, był w stanie nauczyć się układania dwóch pierwszych warstw wyłącznie przez obserwację, śledząc ruchy układanych w danym momencie elementów. Dlatego też każdemu stanowczo odradzam uczenie się na pamięć jakichkolwiek kombinacji potrzebnych aż do tego momentu.
Z chwilą rozpoczęcia układania ostatniej warstwy sytuacja zmienia się jednak drastycznie. I choć teoretycznie każdy sam może opracować sobie metodę układania kostki do końca, zapewniam, że jest w praktyce tak trudne, że tylko nielicznym się powiodło. Właśnie dlatego wszyscy ludzie, których znam i którzy potrafią ułożyć kostkę do końca, układają ostatnią warstwę korzystając z opanowanych pamięciowo sekwencji ruchów. I jak już wspomniałem, najlepszą metodą zapamiętania tych sekwencji okazuje się system cyfrowy, a nie system oznaczeń literowych, który jest jedynym spotykanym w internecie, poza moją witryną oczywiście. System symboliczny jest łatwiejszy w odczycie, ale trudniejszy w zapamiętaniu, i właśnie dlatego proponuję początkującym nauczenie się systemu cyfrowego i korzystanie z niego.
Uwaga: przed rozpoczęciem etapów 4, 5, 6 i 7 konieczne będzie odpowiednie zorientowanie kostki. Pamiętajmy, że możemy nią obracać jak globusem, wokół osi północ – południe. Innymi słowy, w czasie wszelkich manewrów dokonywanych aż do zakończenia układania kostki ściana żółta musi zawsze pozostać skierowana ku górze.
Etap czwarty
Celem czwartego etapu jest nadanie kantom górnej warstwy właściwej orientacji, tj. ułożenie krzyża z kantów o kolorze górnej ściany. Kanty te nie muszą zajmować właściwych pozycji. Takie podejście do problemu, choć wydaje się nienaturalne, jest jednak głęboko pragmatyczne.
Dotąd nie musieliśmy się uczyć żadnych formułek na pamięć, czas jednak dla trening dla pamięci. Nauczymy się też kolejnego, cyfrowego systemu notacji ruchów. Formułki zapisane w tym systemie łatwiej jest bowiem zapamiętać. Nie będziemy za to odtąd stosować graficznych schematów wszystkich kolejnych ruchów, nadszedł bowiem czas, aby zacząć w pełni korzystać z zapisów symbolicznych i cyfrowych.
Twórcy systemu cyfrowego wyszli z założenia, że ściany najlepiej ponumerować zgodnie z porządkiem ich pojawiania się w kolejnych manewrach. Dzięki temu zapamiętanie kombinacji staje się naprawdę proste.
W systemie cyfrowym nie notuje się ruchów o 180° i traktuje się je jak dwa kolejne ruchy tą samą ścianą. Obroty w lewo znaczy się apostrofem albo minusem umieszczonym nad cyfrą, tak jak matematycy zapisują ujemną cechę logarytmu. Kierunki obrotu ścian ustala się tak samo, jak w zapisie symbolicznym – obrót w prawo oznacza ruch zgodny z kierunkiem wskazówek zegara, patrząc wprost na daną ścianę.
Na poniższych schematach ściana żółta jest ścianą górną, ściana niebieska jest ścianą czołową, a ściana czerwona ścianą prawą. Ułamki oznaczają prawdopodobieństwo wystąpienia danego przypadku, liczby pod rysunkami oznaczają numery przypadków. W momencie, gdy skończyliśmy układać dwie warstwy, na ścianie górnej (żółtej) może pojawić się jeden z podanych na schematach układów:
| 1/8 | 3/8 | 3/8 | 1/8 |
|
|
|
|
|
| 1 | 2 | 3 | 4 |
Innymi słowy, na ścianie żółtej pojawiają się bądź wszystkie 4 żółte ścianki kantów (przypadek 4; nie liczymy przecież żółtego środka ściany górnej!), bądź tylko dwie (przypadki 2 i 3), bądź żadna (przypadek 1). Poprawnie złożona kostka Rubika fizycznie nie pozwala na inne możliwości (nie dotyczy to kostki 4×4×4!!!). Jeżeli na twojej kostce widoczny jest inny układ (jeden bądź trzy żółte ścianki kantów), nie da się jej na pewno ułożyć do końca. Ktoś ją rozebrał na części i źle złożył, i teraz jedynym sposobem jest jej ponowne rozłożenie i złożenie.
Oczywiście jest idealnie, jeżeli zaszedł przypadek czwarty, wówczas bowiem pomijamy całkowicie etap bieżący i przechodzimy od razu do etapu piątego. W przypadkach 2 i 3 układamy warstwę górną tak jak na schematach: żółte ścianki na górnej ścianie muszą tworzyć bądź znak minus (przypadek 3), bądź też bumerang skierowany końcami w prawo i w stronę czoło kostki (tj. do nas). Uwaga: kolory ścian czołowej i prawej są zupełnie nieistotne, ważne jest tylko odpowiednie ustawienie ściany górnej.
Umówmy się teraz, że:
- ściana tylna kostki ma numer 1,
- ściana lewa kostki ma numer 2,
- ściana górna kostki ma numer 3.
Upewniwszy się, że ustawienie ściany górnej jest na pewno takie jak na jednym ze schematów, wykonujemy kombinację numer jeden:
1 2 3 2´ 3´ 1´
Oto jej tłumaczenie na język polski: ścianą tylną w prawo (należy tu szczególnie uważać, co to właściwie znaczy!), ścianą lewą w prawo, ścianą górną w prawo, ścianą lewą w lewo, ścianą górną w lewo, ścianą tylną w lewo. Zapis symboliczny w wersji polskiej: TLGL'G'T', w wersji angielskiej: BLUL'U'B'.
Każdy musi sam ocenić, czy łatwiej mu zapamiętać sekwencję symboli, czy sekwencję cyfr, tak czy inaczej jednak zapamiętać ją trzeba (a przynajmniej jest to wskazane).
Wykonajmy więc podaną kombinację ruchów. Jeszcze raz podkreślam, że należy dobrze się zastanowić, w którą stronę obracamy ściany, zwłaszcza ścianę tylną. Nieprawidłowe wykonanie ruchu jest bardzo częste u początkujących. Podpowiedź: obrót ściany tylnej w prawo powoduje, że narożnik położony w wierzchołku u styku ścian prawej, tylnej i górnej wędruje do góry, a następnie do pozycji na styku ścian tylnej, lewej i górnej. Z punktu patrzenia układającego wygląda to jak ruch w lewo, jednak jest w rzeczywistości obrotem ściany tylnej zgodnie z kierunkiem wskazówek zegara. Umiejętność wykonywania obrotów ściany tylnej trzeba sobie po prostu przyswoić poprzez ćwiczenia. Kara za błąd jest dotkliwa: prawdopodobnie kostkę trzeba będzie układać od nowa!
Jeżeli zaczynaliśmy od pozycji 3 i nie popełniliśmy błędu, na górnej ścianie powinien widnieć krzyż z kantów (pozycja 4).
Jeżeli zaczynaliśmy od pozycji 2, musimy wykonać podaną kombinację dwukrotnie. Po pierwszym wykonaniu dochodzimy do pozycji 3, i dopiero ponowne wykonanie prowadzi do pozycji 4.
Jeżeli zaczynaliśmy od pozycji 1, otrzymujemy co prawda żółty bumerang, jednak inaczej zorientowany niż w pozycji 2, bo ku tyłowi i ku lewej. W takim wypadku musimy całą kostkę lub tylko jej górną ścianę (to bez znaczenia) obrócić o 180° i wykonać podaną kombinację jeszcze dwa razy, aby w końcu dojść do pozycji 4. Uwaga: nieobrócenie ściany górnej (lub kostki) nie doprowadzi nas do końcowego rezultatu!
Zauważmy jeszcze, że sekwencja zaczyna się od ruchu „tylna w prawo”, a kończy „tylna w lewo”. Gdy zatem sekwencję wykonujmy dwukrotnie, można oba te ruchy pominąć. Początkującym odradzam jednak tego typu skróty. Najważniejsze, by wyrobić sobie odruch poprawnego wykonywania całej kombinacji. Dopiero gdy jest się pewnym, można próbować upraszczać sobie życie.
Po osiągnięciu biegłości w posługiwaniu się kombinacją numer jeden, wychodząc od pozycji 2 możemy zatem kręcić 1 2 3 2´ 3´ 2 3 2´ 3´ 1´. W polskim zapisie symbolicznym możemy zapisać to samo jako T·(LGL'G')2·T'; kropka nie ma żadnego znaczenia, służy tylko do oddzielenia podobnych partii manewru, dwójka oznacza dwukrotne powtórzenie fragmentu w nawiasie. To samo w zapisie angielskim: B·(LUL'U')2·B'. Wychodząc zaś od pozycji 1 należy wykonać 1 2 3 2´ 3´ 1´3 3 1 2 3 2´ 3´ 2 3 2´ 3´ 1´ czyli T·LGL'G'·T'·G2·T·(LGL'G')2·T' (ang. B·LUL'U'·B'·U2·B·(LUL'U')2·B'). Oczywiście nie ma najmniejszego sensu, by uczyć się tych długich kombinacji na pamięć, należy jedynie biegle opanować kombinację numer jeden.
Istnieje jednak inne rozwiązanie pozycji nr 2, warte zapamiętania z uwagi na prostotę. Wystarczy bowiem wykonać kombinację numer jeden od tyłu, zmieniając kierunek każdego z obrotów, co daje 1 3 2 3´ 2´ 1´ czyli TGLG'L'T' (ang. BULU'L'B'). Kombinacja ta jest na tyle podobna do kombinacji numer jeden, że zapamiętanie jej nie powinno sprawić kłopotu. Jednakże umiejętność jej stosowania nie jest potrzebna do ułożenia kostki: zamiast niej wystarczy dwukrotnie zastosować kombinację numer 1.
Po opanowaniu sztuki orientowania kantów na ścianie górnej przechodzimy do etapu następnego. Oczywiście zdarzyć się może i tak (choć w bardzo rzadkich przypadkach), że cała kostka jest już ułożona, a wtedy… cóż, możemy ją trochę pomieszać i poćwiczyć układanie od nowa.
Etap piąty
Celem piątego etapu jest umieszczenie kantów górnej warstwy na swoich miejscach. Kanty te są już właściwie zorientowane (dzięki etapowi czwartemu). Aby dokonać odpowiedniego ich ulokowania, musimy wprowadzić nowe oznaczenie 4 dla ściany prawej.
A zatem:
- ściana tylna kostki ma numer 1,
- ściana lewa kostki ma numer 2,
- ściana górna kostki ma numer 3,
- ściana prawa kostki ma numer 4.
Przed rozpoczęciem etapu piątego musimy przede wszystkim tak przekręcić ścianą górną i tak ustawić całą kostkę, aby dobrze ułożone były kanty prawy i tylny (tworzą one zarys litery L), o ile to tylko możliwe. Innymi słowy, staramy się, aby uzyskać jeden z pokazanych poniżej układów (kolory mogą się oczywiście różnić). Tym razem każdą z pozycji pokazujemy na dwóch schematach:
| Przypadek | Widok ścian górnej, czołowej i prawej |
Widok ścian górnej, tylnej i lewej |
Opis | |
|---|---|---|---|---|
| 1 | 1/6 |
|
|
ułożone kanty lewy i prawy |
| 2 | 2/3 |
|
|
ułożone kanty tylny i prawy |
| 3 | 1/6 |
|
|
wszystkie kanty ułożone |
Przypadek 3 oznacza, że możemy przejść do kolejnego etapu. W przeciwnym wypadku, upewniwszy się, że ustawienie ściany górnej jest takie jak na jednym ze schematów, wykonujemy kombinację numer dwa:
4 3 4´ 3 4 3 3 4´ 3
Przypominam, że 4 oznacza ścianę prawą, 3 – ścianę górną. Zapis symboliczny w wersji polskiej: PGP'GPG2P'G, w wersji angielskiej: RUR'URU2R'U.
I znów, kombinację tę trzeba zapamiętać. Na szczęście nie jest to zbyt trudne. Warto zauważyć, że kręcimy na przemian ścianą prawą i górną, przy czym ścianą górną kręcimy stale w prawo (za trzecim razem dwukrotnie), zaś ścianą prawą na przemian w prawo i w lewo.
Wykonajmy więc podaną kombinację ruchów – mam nadzieję, że nie są do tego celu potrzebne żadne pomocnicze schematy. Jeżeli zaczynaliśmy od pozycji 2 i nie popełniliśmy błędu, wszystkie kanty zostaną ułożone (pozycja 3).
Jeżeli zaczynaliśmy od pozycji 1 (poprawnie ułożone kanty lewy i prawy), po zakończeniu wykonywania kombinacji musimy dodatkowo przekręcić górną ścianą w prawo, a następnie przekręcić w prawo cała kostką. Zamiast uczyć się tej dodatkowej zasady wystarczy zapamiętać, że należy po prostu ponownie doprowadzić kostkę do jednej z podanych w tabeli pozycji. W wyniku tych dodatkowych operacji nasza kostka znajdzie się w pozycji 2 i będziemy mogli ponownie wykonać kombinację numer dwa.
Po opanowaniu sztuki ustawiania kantów na ścianie górnej przechodzimy do etapu następnego. Oczywiście zdarzyć się może i tak (choć w rzadkich przypadkach), że cała kostka jest już ułożona, a wtedy… cóż, możemy ją trochę pomieszać i poćwiczyć układanie od nowa.
Etap szósty
Celem szóstego etapu jest umieszczenie narożników górnej warstwy na swoich miejscach, choć niekoniecznie we właściwej orientacji. Przypominamy, że wszystkie kanty kostki są już właściwie ułożone i zorientowane, co sprawia, że ściana górna jest niejako zablokowana. W celu przygotowania do ułożenia narożników będziemy więc obracać całą kostką, a nie ścianą górną (co do tej pory było możliwe). Kostką obracamy jak globusem: żółta ściana musi cały czas pozostać ścianą górną.
Przypominamy też sobie po raz kolejny oznaczenia ścian, których dotąd używaliśmy:
- ściana tylna kostki ma numer 1,
- ściana lewa kostki ma numer 2,
- ściana górna kostki ma numer 3,
- ściana prawa kostki ma numer 4.
A zatem przed rozpoczęciem etapu szóstego sprawdzamy, czy którykolwiek z narożników ściany górnej nie znajduje się już na dobrej pozycji, choć niekoniecznie w dobrym położeniu. Jeżeli taki znajdziemy, obracamy całą kostkę tak, by ten dobrze ułożony narożnik znalazł się w wierzchołku tylnym, prawym, górnym (pozycja podobna jak pozycja dwóch dobrych kantów na etapie piątym).
Wyjaśnijmy to na przykładzie. Poniższe schematy pokazują tę samą kostkę z dwóch pozycji:
| ściana górna, czołowa i prawa | ściana górna, prawa i tylna |
|---|---|
|
|
|
Narożnik żółto-niebiesko-czerwony (w centrum lewego schematu) ma co prawda właściwą orientację (żółtą ścianką ku górze), nie zajmuje jednak swojej pozycji (powinien znajdować się na ścianie niebieskiej i czerwonej, a znajduje się na ścianie pomarańczowej i zielonej). Takie narożniki nas nie interesują.
Narożnik pomarańczowo-niebiesko-żółty (w centrum prawego schematu) ma co prawda złą orientację, jednak znajduje się na swojej pozycji – należy do ściany pomarańczowej i niebieskiej. Właśnie taki narożnik umieszczamy w wierzchołku tylnym, prawym, górnym. Po raz kolejny przypominam, że nie wolno nam przy tym kręcić samą ścianą górną, której kanty są już przecież ułożone – musimy obrócić cała kostką.
Ogólnie rzecz biorąc, może się zdarzyć, że:
- żaden narożnik nie jest dobrze ułożony (poz. 1) – wówczas ustawiamy kostkę dowolnie (oczywiście ścianą żółtą do góry); prawdopodobieństwo wystąpienia takiej możliwości wynosi 1/4;
- jeden narożnik jest dobrze ułożony (poz. 2 – ustawiamy kostkę tak, by znalazł się on w pozycji prawej tylnej); prawdopodobieństwo takiego przypadku wynosi 2/3;
- wszystkie narożniki będą już dobrze ułożone (poz. 3 – wtedy oczywiście przechodzimy do ostatniego etapu orientowania narożników); prawdopodobieństwo takiego przypadku wynosi 1/12.
Nie istnieje fizyczna możliwość, aby ułożyć kostkę Rubika, w której dokładnie dwa narożniki są przestawione miejscami, a wszystkie kanty są na właściwych miejscach i mają właściwą orientację. Taka kostka musiała być rozłożona i złożona źle. Uwaga ta naturalnie dotyczy tylko kostek 3×3×3, ale taką kostkę przecież układamy.
Po właściwym zorientowaniu kostki wykonujemy kombinację numer trzy:
2 3´ 4´ 3 2´ 3´ 4 3
Przypominam, że 2 oznacza ścianę lewą, 3 – ścianę górną, 4 – ścianę prawą. Zapis symboliczny kombinacji: pol. LG'P'GL'G'PG, ang. LU'R'UL'U'RU.
Podobnie jak poprzednie, kombinację tę trzeba zapamiętać, i po raz kolejny nie okaże się to chyba zbyt trudne. Zwróćmy uwagę, że ruchy ścian lewej i prawej są jakby „zsynchronizowane”: w obu przypadkach wyciągamy na górę krawędź tylną, a następnie ją chowamy. Pomiędzy tymi ruchami kręcimy ścianą górną, naprzemian w lewo i w prawo.
Wykonajmy więc podaną kombinację ruchów – mam nadzieję, że nie są do tego celu potrzebne żadne pomocnicze schematy. Czekać nas może jednak mała niespodzianka.
Otóż jeżeli zaczynaliśmy od pozycji 2 i nie popełniliśmy błędu, tylko w połowie przypadków wszystkie kanty zostaną ułożone (pozycja 3). W pozostałych sytuacjach musimy wykonać kombinację jeszcze raz, nie zmieniając położenia kostki.
Jeżeli natomiast zaczynaliśmy od pozycji 1, po zakończeniu wykonywania kombinacji musimy kostkę odpowiednio zorientować, aby przejść do pozycji 2. I wówczas znów tylko w 50% przypadków osiągniemy poz. 3, a w pozostałych sytuacjach będziemy musieli zastosować kombinację numer trzy po raz trzeci, tym razem nie zmieniając położenia kostki.
Zaawansowani adepci sztuki układania kostki mogą tę sytuację nieco zoptymalizować. Może jednak najpierw łyk teorii.
Otóż kombinacja numer trzy jest tzw. 3-cyklem, to znaczy powtórzona trzy razy (bez żadnych dodatkowych obrotów!) pozwoli osiągnąć stan wyjściowy. Jej działanie można przedstawić w postaci zapisu (gpc, ltg, lgc) – już tłumaczę, co dokładnie to oznacza. Trzyliterowe symbole oznaczają poszczególne narożniki, a litery odpowiadają symbolom ścian. A zatem gpc to narożnik umieszczony u zbiegu ściany górnej, prawej i czołowej.
Zapis (gpc, ltg, lgc) mówi nam, że narożnik u zbiegu ściany górnej, prawej i czołowej przechodzi na miejsce narożnika u zbiegu ścian lewej, tylnej i górnej, ten z kolei przechodzi na miejsce narożnika lewego, górnego, czołowego, a ten przechodzi do pozycji pierwszego z narożników (i tak cykl się zamyka). Co więcej, z zapisu tego wynika, że górna ścianka narożnika gpc staje się lewą ścianką narożnika ltg, a prawa ścianka gpc – tylną ścianką ltg (innymi słowy, kolejność liter jest istotna). Działanie kombinacji numer trzy przedstawia schemat (widok ściany górnej, czołowej i prawej):

Zauważmy, że aby nie wykonywać kombinacji dwukrotnie, wystarczy odwrócić kierunek zmian. W tym celu wykonujemy kombinację od tyłu, zmieniając dodatkowo kierunek wszystkich obrotów na przeciwny. W naszym przypadku, zamiast 2 3' 4' 3 2' 3' 4 3 będziemy więc mieli 3' 4' 3 2 3' 4 3 2', w zapisie symbolicznym pol. G'P'GLG'PGL', ang. U'R'ULU'RUL'. Efekty takiej odwróconej kombinacji możemy zapisać jako (gpc, lgc, ltg) i zobrazować poniższym schematem:

Uwaga: kombinacja odwrotna jest przeznaczona dla chętnych; zamiast niej zawsze można wykonać dwukrotnie niezmodyfikowaną kombinację numer trzy. Nie trzeba jej zatem zapamiętywać, nie jest w sumie do niczego potrzebna (poza tym, że przyśpiesza ułożenie kostki, jeśli zostanie właściwie użyta).
Warto jeszcze podkreślić, że jeśli na początku żaden z narożników nie zajmuje właściwej pozycji (poz. 1), musimy wykonać kombinację numer trzy (prostą, ale jeśli ktoś chce, może odwrotną), po czym ponownie sprawdzić ułożenie narożników, umieścić właściwie ułożony w prawym tylnym rogu, i wykonać kombinację numer trzy jeszcze raz. Dopiero za drugim razem można zdecydować, czy korzystniej będzie kręcić zwykłą kombinację numer trzy, czy też może „nadobowiązkową” kombinację odwrotną.
Po opanowaniu sztuki ustawiania narożników na ścianie górnej przechodzimy do ostatniego już, siódmego etapu. Oczywiście zdarzyć się może i tak (w jednym przypadku na 27), że cała kostka jest już ułożona, a wtedy… cóż, możemy ją trochę pomieszać i poćwiczyć układanie od nowa.
Etap siódmy
Celem ostatniego, siódmego etapu jest nadanie narożnikom górnej warstwy właściwej orientacji, tj. obrócenie ich kolorem górnej ściany do góry. Przed przystąpieniem do etapu siódmego wszystkie części kostki są już na swoich miejscach, przy czym wszystkie kanty są także właściwie zorientowane.
Przypominamy sobie poznane oznaczenia ścian i wprowadźmy dwa ostatnie oznaczenia:
- ściana tylna kostki ma numer 1,
- ściana lewa kostki ma numer 2,
- ściana górna kostki ma numer 3,
- ściana prawa kostki ma numer 4,
- ściana czołowa kostki ma numer 5,
- ściana dolna kostki ma numer 6.
Podobnie jak na poprzednich etapach, i teraz nie każda orientacja narożników jest dopuszczalna. Możliwe są tylko następujące sytuacje (w nawiasie prawdopodobieństwo zaistnienia):
- wszystkie 4 narożniki są źle zorientowane, przy czym 2 skręcone są w prawo, a 2 w lewo (2/9);
- 3 narożniki są źle zorientowane, wszystkie trzy w tę samą stronę (8/27);
- 2 narożniki są źle zorientowane: jeden skręcony jest w prawo, a drugi w lewo (4/9);
- wszystkie narożniki są dobrze zorientowane (1/27); oczywiście wówczas cała kostka jest już ułożona.
Autor wymienionej na stronie z linkami książki o kostce, W. Hintze, nazywa drugą sytuację barionem, a trzecią mezonem. Sytuacja pierwsza oznacza istnienie dwóch mezonów. Tak naprawdę jest zupełnie bez znaczenia, która z sytuacji ma miejsce (oczywiście z wyjątkiem sytuacji czwartej), gdyż nasze postępowania będzie właściwie takie samo. Będziemy po prostu odwracać kolejne narożniki, burząc przy okazji wiele elementów już ułożonych, jednak gdy ostatecznie zakończymy odwracanie wszystkich narożników, okaże się, że kostka jest już całkowicie ułożona.
We właściwym zorientowaniu narożników pomoże kombinacja numer cztery:
5 6 5´ 6´ 5 6 5´ 6´
lub bliźniacza kombinacja odwrotna:
6 5 6´ 5´ 6 5 6´ 5´
Przypominam, że 5 oznacza ścianę czołową, 6 – ścianę dolną. Zapis symboliczny kombinacji prostej: pol. (CDC'D')2, ang. (FDF'D')2, zapis kombinacji odwrotnej: pol. (DCD'C')2, ang. (DFD'F')2. Obie kombinacje warto zapamiętać, a z uwagi na ich prostotę nie powinno to spowodować problemów. Podobnie jak na etapie 6, do ułożenia kostki wystarcza jednak w zupełności tylko jedna z tych kombinacji.
Kombinacja numer cztery, podobnie jak kombinacja numer trzy, jest 3-cyklem. Choć wydaje się bardzo prosta, ma w rzeczywistości bardzo niemiłe właściwości.
- Przede wszystkim, musimy bardzo uważać na obroty ściany dolnej – dobrze poćwiczyć sobie najpierw, co właściwie oznacza obrót tej ściany w prawo i w lewo (patrząc na kostkę od góry odnosimy wrażenie, że kierunek obrotu jest odwrotny!). Pomyłka na tym etapie układania kostki jest bardzo bolesna i oznacza rozpoczynanie całej pracy od nowa w momencie, gdy niemal dotarliśmy do końca.
- Nie wolno zapominać o końcowym obrocie ścianą dolną w przypadku kombinacji prostej. Jeżeli wykonujemy kombinację po raz pierwszy, kostka jest w stanie chaosu i możemy zapomnieć o tym obrocie, zwłaszcza, że odwracany narożnik uzyskał właściwą orientację już w ruchu przedostatnim. Doświadczenie początkujących kostkarzy pokazuje, że właśnie ten nieszczęsny obrót jest przyczyną bardzo niemiłych w skutkach pomyłek.
- Jak już było wspomniane, w przeciwieństwie do kombinacji numer jeden, dwa i trzy, jednokrotne użycie kombinacji numer cztery wywołuje na kostce niezły galimatias, a to znakomicie utrudnia pracę, gdyż trzeba obracać „na ślepo”, to znaczy wyłącznie według kombinacji (i dlatego trzeba ją opanować perfekcyjnie, by się nie pomylić).
- Dobrze jest umieć rozpoznawać, czy dla danego narożnika właściwsza będzie kombinacja prosta (5 6…) czy też może odwrotna (6 5…). Błędny wybór nie grozi żadnymi konsekwencjami, poza koniecznością wykonywania większej ilości obrotów. Ale właśnie ta okoliczność wydłuża niepotrzebnie siódmy etap i w ten sposób zwiększa prawdopodobieństwo popełnienia błędu.
- Wreszcie zmienia się nasze miejsce robocze w porównaniu z etapem piątym i szóstym, a więc pozycja, w której musimy umieścić obracany narożnik. Tym razem umieszczamy go w wierzchołku, w którym zbiegają się ściany górna, prawa i czołowa.
Poniższe schematy pokazują, w jakiej sytuacji lepiej zacząć od kombinacji prostej, a w jakiej od kombinacji odwrotnej. Schematy ukazują sytuację numer 1 (dwa mezony) i uwidaczniają ścianę czołową, górną i prawą. Narożnik przeznaczony do obrotu znajduje się w samym centrum:
|
|
|
| ścianka żółta narożnika na ścianie czołowej | ścianka żółta narożnika na ścianie prawej |
| kombinacja prosta | kombinacja odwrotna |
| 5 6 5´ 6´ 5 6 5´ 6´ | 6 5 6´ 5´ 6 5 6´ 5´ |
Aby uniknąć potencjalnych problemów, najlepiej przyjąć następujące zasady działania. Po pierwsze, przed rozpoczęciem wykonywania kombinacji numer cztery musimy zdecydować, jak ustawić kostkę (oczywiście górna i dolna ściana nie może zmienić swojego położenia, chodzi jedynie o to, która ściana będzie czołową, która prawą itd.). Gdy już podejmiemy decyzję, nie wolno nam będzie w ogóle poruszać kostką aż do samego końca. Przez cały czas orientowania narożników, aż do całkowitego ułożenia, trzymamy więc kostkę sztywno, nie przekręcamy jej, a narożnik gpc (górna – prawa – czołowa) pozostaje cały czas naszym „narożnikiem manewrowym”.
Nie należy się w ogóle przejmować, jaki układ tworzą narożniki. Po jednorazowym wykonaniu kombinacji numer cztery i stwierdzeniu, że układany narożnik rzeczywiście uzyskał prawidłową orientację nie przejmujemy się zdemolowaną kostką, lecz przekręcamy górną ścianą tak, aby w pozycji manewrowej znalazł się kolejny narożnik przeznaczony do odwrócenia. Wybieramy właściwą kombinację (i nie przejmujemy się zupełnie potencjalną pomyłką w wyborze) i wykonujemy ją. Postępujemy w ten sposób tak długo, aż kostka będzie ułożona (maksymalnie cztery razy, a jeśli wybraliśmy niewłaściwą kombinację, to nawet więcej) – zauważymy na pewno, kiedy pozostał nam już tylko wyrównujący obrót ścianą górną.
Jeśli na przykład oba odwrócone narożniki tworzyły mezon (tj. były odwrócone w przeciwnym kierunku), to raz wykonywaliśmy kombinację prostą, a raz odwrotną. To z kolei spowodowało cofnięcie wszystkich zmian i całego chaosu, który pojawił się na kostce. Możemy teraz obrócić górną ścianą do właściwego położenia… i albo okaże się, że kostka już jest ułożona (wyjściowa była sytuacja 3), albo też będziemy musieli zająć się w identyczny sposób drugim mezonem (wyjściowa była sytuacja pierwsza, ale teraz mamy sytuację trzecią).
Jeśli orientacja narożników tworzyła barion (sytuacja 2), i odwracając dwa narożniki wykonaliśmy dwa razy tę samą kombinację (dwa razy prostą lub dwa razy odwrotną), to jeszcze jeden narożnik musi być źle zorientowany. Znajdziemy go, kręcąc ścianą górną. Gdy już znajdzie się w położeniu manewrowym, wykonujemy właściwą kombinację jeszcze raz. Ponieważ kombinacja jest 3-cyklem, trzykrotne jej wykonanie cofnie wszystkie niekorzystne zmiany, jakim uległa kostka.
Jeśli nie popełniłeś błędu, masz oto w ręce całkowicie ułożoną kostkę. Jeśli zaś popełniłeś… no cóż.. Tak czy inaczej, warto spróbować jeszcze raz, i jeszcze raz… aż do osiągnięcia mistrzostwa.
Dla mistrzów zaś mam kilka propozycji. Po pierwsze, zapraszam na kurs układania kostki drugą metodą, dla zaawansowanych. W metodzie tej, należącej do grupy „najpierw narożniki”, trzeba już zapamiętać więcej kombinacji, a niektóre z nich będą naprawdę nieprzyjemne. Układanie niektórych elementów sprawi jednak więcej satysfakcji, będzie bowiem więcej kombinowania, a mniej korzystania z gotowych recept. Podkreślam, że chcąc zacząć układanie kostki tą drugą metodą, dobrze jest najpierw osiągnąć biegłość w metodzie dla początkujących. Nabyte umiejętności bardzo się bowiem przydadzą.
Po drugie, przedstawię zbiór różnych alternatywnych algorytmów, które bądź to przyśpieszają układanie kostki w niektórych sytuacjach, bądź też dają możliwość pewnych odchyleń od metody pierwszej, tj. stosowania systemu „warstwa po warstwie”, jednak z inna kolejnością etapów.
Po trzecie, zaproponuję kurs układania kostek o większych rozmiarach, które jak słusznie się można domyślić, stwarzają układającemu wiele nowych wyzwań i wymagają zastosowania dodatkowych metod, niepotrzebnych przy kostce Rubika.
Wreszcie na koniec zajmiemy się kostkową twórczością, a więc układaniem przyciągających oko wzorków na ułożonej kostce.
Zapraszam!
Artykuł został opublikowany także na witrynie autora pod adresem http://grzegorj.5v.pl/kostka/index.html