Chłopiec ma wspaniałą kolejkę pozwalającą uczyć się programowania. Pewnego dnia wizyta cioci inspiruje go do napisania nowego programu. Okazuje się jednak, że wyników nie ma ...
Pewnego dnia przyszła ciocia Magdzia. Rozpoczęła się rozmowa na tematy rodzinne, aż w pewnym momencie Ciocia powiedziała:
- Tak, właśnie jest w pracy - odpowiedziała mama.
|
|
- A jaki masz problem ? - zapytała z zainteresowaniem.
- Jak wiesz zajmuję się urządzaniem ogródków. I właśnie wczoraj przyszedł do mnie pewien zamożny gość z niezwykłym problemem. Chce mianowicie by obsadzić mu krzewami róż prostokątny plac z przejściem pośrodku - zaczęła opowiadać Ciocia.
- I cóż w tym niezwykłego? Przecież już nieraz wykonywałaś podobne prace - zapytała z niedowierzaniem mama.
- Tak. Ale ten gość chce by krzewy były rozmieszczone w dokładnie równych odległościach w obydwu trójkątnych polach. Wzięłam rozmiary placu, ale nie mogę znaleźć takich trójkątów. Więc pomyślałam sobie, że może pomógłby komputer.
Na te słowa słuchający dotąd bez zainteresowania Piotruś nagle przestał jeść i zaczął wpatrywać się w gościa po czym poprosił:
- A mogłabyś Ciociu narysować plan tego placyku.
Ciocia Magdzia wzięła do ręki długopis i zaczęła rysować. Po czym narysowawszy powiedziała.
- Narysowałam przykładowe rozmieszczenie kępek kwiatów, ale tu już z daleka widać, że odległości są nierówne. Trzeba odpowiednio dobrać proporcje boków trójkątów i ilości klombów by wszystko się zgadzało, ale tego ja już nie potrafię.
- Ale to przecież jest proste. To są boki trójkątów prostokątnych, dla których znane jest twierdzenie Pitagorasa. Wystarczy więc dobrać taką trójkę liczb całkowitych by równanie było spełnione i cześć - po chwili zastanowienia wykrzyknął Piotrek.
- Dobrze, dobrze. Ja już tak próbowałam ale to wcale niełatwo znaleźć takie trzy liczby całkowite, które spełniają warunek - odpowiedziała mu Ciocia.
- Ale przecież ja mam kolejkę, która nie takie rzeczy potrafi liczyć. Więc zaraz zestawię tory i przyniosę Ci wyniki - zapewnił i ruszył do pracy.
- Najpierw, wstawię warunek, który sprawdza czy trzy liczby spełniają warunek bycia trójkątem prostokątnym i jeśli tak to wynik będzie wyświetlany - mówił zestawiając tory.
- A ile ma być tych róż ? - zwrócił się z zapytaniem do Ciotki.
- Między 80 a 120 - odpowiedziała mu Ciotka.
- A więc otoczę tę instrukcję trzema pętlami na wartości kolejnych boków tak by dwukrotna ich suma mieściła się w zadanym przedziale - mówił dalej Piotr.
- No gotowe - powiedział w końcu i uruchomił kolejkę.
Kolejka zaczęła krążyć, a tymczasem nadchodził zmierzch. Po godzinie nie było jeszcze wyników.
- Tato. Czemu ona nie potrafi rozwiązać problemu róż - powiedział w końcu.
- Potrafi. Tylko robi to zbyt wolno. Jest po prostu bardzo powolnym komputerem - wyjaśniał Ojciec.
- I nic się nie da zrobić ? - zapytał smutnie Piotr.
- Tego nie powiedziałem. Dla każdego problemu możemy wziąć rozwiązanie pierwsze z brzegu lub zastanowić się nad nim dogłębnie i próbować podać rozwiązanie najsprawniejsze z możliwych to jest wymagające jak najmniej kroków by znaleźć wynik - powiedział Ojciec.
- A mógłbyś się zastanowić czy istnieje lepsze rozwiązanie problemu róż ? - poprosił chłopiec.
- Może spróbujemy zrobić to razem. Zgoda ?
- No pewnie. Jestem gotów - raźno odpowiedział Piotr.
- Najpierw napisz równanie Pitagorasa - powiedział, a Piotr posłusznie napisał:
![]()
- A teraz przenieśmy jeden z boków na drugą stronę:
![]()
- Czy przypominasz sobie to wyrażenie z prawej strony ? - zapytał Ojciec.
- Ależ tak. To jest wynik skróconego mnożenia. Zaraz to rozpiszę:
![]()
- No właśnie. A teraz wylicz a - polecił Ojciec a chłopiec posłusznie zapisał:
![]()
- A teraz pomyśl. Jakie to muszą być liczby c-b i c+b by a było liczbą całkowitą? - zapytał Ojciec.
- Zarówno c-b jak c+b muszą być kwadratami jakichś liczb całkowitych.
- No, nie jest to do końca prawdą bowiem zarówno a jak c-b i c+b mogą mieć jeszcze wspólny podzielnik. Jednak dla naszych rozważań wygodnie jest przyjąć, że ten podzielnik zawsze jest równy jeden, bowiem rozwiązania powstające przez przemnożenie boków przez stałą są mało „eleganckie”. Przy tym założeniu możesz wprowadzić zmienne pomocnicze:
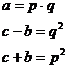
- Bardzo dobrze. Teraz zapisz jak wyliczać na podstawie p i q wartości boków trójkąta - znowu polecił Ojciec:
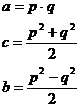
- Widzisz teraz wystarczy przeszukiwać p i q (gdzie zawsze p > q) by otrzymywać boki trójkąta. Musisz teraz tylko ustalić zakres przeszukiwania.
- To proste. Najpierw Ci napiszę ile będziemy mieć róż - odpowiedział chłopiec pisząc:
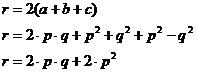
- Teraz wystarczy podstawić za q 1 i wyliczyć p na podstawie minimalnej liczby róż, a potem wyliczyć z p wartość :q - objaśniał dalej.
- Tylko zauważ, że kolejka nie ma operatora pierwiastkowania i będziemy musieli wyliczyć p badając kolejne liczby naturalne od 1 dla spełnienia warunku przewyższania minimalnej liczby róż. Teraz to już sobie poradzisz z programem. Ja idę z mamą na spacer - powiedział Ojciec zostawiając Piotra pochylonego nad kolejką.
To fragment podręcznika pt.: "Od zabawy kolejką do programowania" pomagającego w posługiwaniu się edukacyjnym programem TRAIN 1.5.

