Rozwiązanie problemów Davida Hilberta z 1900 roku kusiło wielu matematyków. W 1936 roku Alan Turing rozstrzygnął jeden z nich konstruując ... genialny model matematyczny komputera
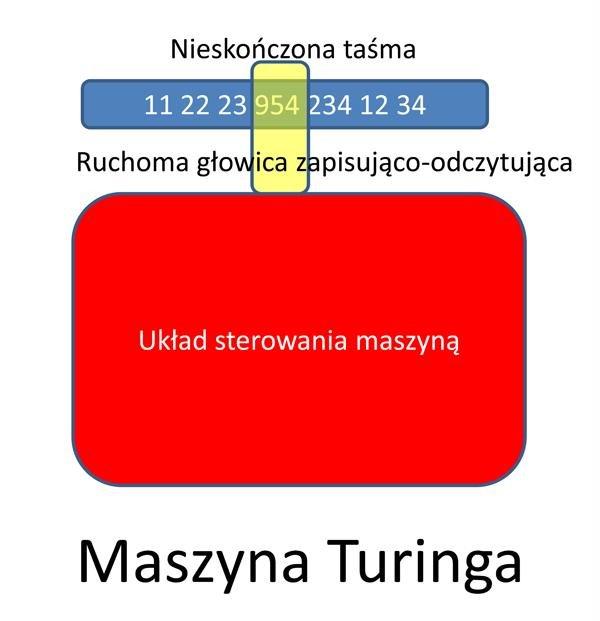
Pracujący w Cambridge matematyk Alan Turing napisał w 1936 roku swoją prawdopodobnie najważniejszą pracę matematyczną. Wprowadził w niej abstrakcyjną maszynę, która była w stanie wykonywać zaprogramowane matematyczne operacje, czyli tak zwany algorytm. Maszyna mogła wykonać jednak tylko jeden, określony algorytm, na przykład mogła wykonać następujący ciąg operacji: podnieść liczbę do kwadratu, podzielić, dodać, odjąć. Według Turinga liczby miały być podawane maszynie za pomocą papierowej taśmy podobnej do taśmy z melodią zapisaną dla pianoli. Podobno Turing wzorował się na znanej mu z zajęć matki maszynie do pisania. Lecz jego maszyna działała tylko na jednym, potencjalnie nieskończonym, wierszu. Potrafiła też przesuwać głowicę w lewo i w prawo nieskończonej taśmy zadrukowując ją za każdym razem bez śladu poprzedniego zapisu lub tylko odczytując zapis by kierować dalszą pracą maszyny. W swojej pracy Turing opisał wiele takich maszyn, które przez naśladowców uzyskały wspólne miano maszyn Turinga. Następnie Turing opracował tak zwaną Uniwersalną Maszynę Turinga, która w zależności od instrukcji zapisanej na taśmie, miała wykonywać dowolne zestawienie podstawowych operacji prowadzace do szerokiego zbioru liczb stanowiących wynik działania. Maszyna zaopatrzona w program do naśladowania wszystkich możliwych tego rodzaju obliczeń, nazwana przez Turinga uniwersalną, stanowi teoretyczny projekt komputera cyfrowego. Jest to uboczny, ale doniosły dla informatyki wynik Turinga.
Wynik główny należy do logiki i podstaw informatyki. Jest nim dowód, że dla każdej maszyny istnieje liczba, której ona nie jest w stanie obliczyć, a więc że istnieją w matematyce problemy nierozstrzygalne. Wynik ten uzyskał Turing dzięki metodzie kodowania formuł-programów w postaci liczb naturalnych (której wzór dał Gödel w 1931 r.). Dzięki temu, przy zastosowaniu tzw. dowodu przekątniowego Cantora, staje się widoczne, że zbiór wszystkich maszyn (zdolnych obliczać z dowolną dokładnością nieskończone rozwinięcia dziesiętne), jako równoliczny ze zbiorem liczb naturalnych (co widać dzięki zakodowaniu), jest przeto mniej liczny niż zbiór wszystkich liczb mających takie rozwinięcia. A więc istnieją liczby nie dające się policzyć na żadnej maszynie.
W ten sam sposób udowodnił, że nie istnieje algorytm pozwalający odpowiedzieć na pytanie dotyczące nierozstrzygalności każdego innego twierdzenia, a zatem nawet uniwersalna maszyna Turinga nie była w stanie zidentyfikować wszystkich nierozstrzygalnych stwierdzeń. Było to ostateczne rozwiązania zagadnienia nierozstrzygalności wprowadzonego do logiki matematycznej przez Kurta Gödla. W tej samej pracy Turing przedstawił schemat pierwszego komputera przygotowany w oparciu o prace Charlesa Babbage'a i jego projekt Maszyny Różniczkowej nr 2. Był to projekt, którego realizacja wykraczała poza możliwości ówczesnej techniki, jednakże z inżynierskiego punktu widzenia był on zupełnie prawidłowy. Dzięki pracy O liczbach obliczalnych, w wieku 26 lat, Turing został uznany za jednego z najlepszych matematyków świata. Bardzo szybko robił karierę naukową, został nawet członkiem King's College.

