Przedstawię Wam przybliżoną konstrukcję geometryczną konstruowalną środkami klasycznymi (linijka i cyrkiel) przy pomocy, której można dzielić kąty z przedziału (0;180> na dowolną liczbę części. Jest to konstrukcja mojego autorstwa. Trysekcja przybliżona wykonana tą konstrukcją w pierwszym przedziale jest 4 razy dokładniejsza od konstrukcji Steinhausa.
Żeby podzielić dany kąt środkowy AOB okręgu o środku O i promienu r = OA = OB na n części, należy najpierw wyznaczyć odpowiedni punkt na dwusiecznej tego kąta, a następnie połączyć odcinkiem otrzymany punkt z punktem przecięcia się okręgu z przedłużeniem jednego z ramion kąta. Punkt przecięcia się odcinka i okręgu podzieli dany kąt AOB na n-tą część. Aby to zobrazować wykonam teraz przybliżoną trysekcje.(rys.1)
Przybliżona trysekcja
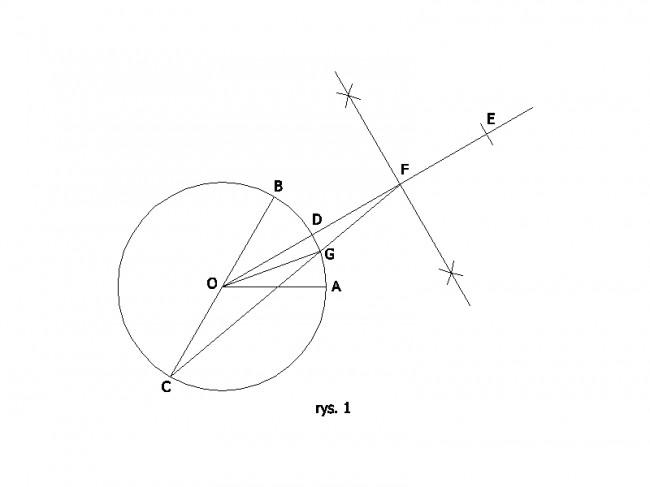
Opis czynności:
1. Rysujemy okrąg o środku O i promienu r oraz kąt środkowy AOB, gdzie r = OA = OB
2. Przedłużamy jedno z ramion kąta i punkt przecięcia się z okręgiem oznaczamy C
3. Kreślimy dwusieczną kąta AOB i otrzymujemy punkt D
4. Na dwusiecznej odkładamy odcinek DE = CD
5. Kreślimy symetralną odcinka DE i otrzymujemy punkt F
6. Rysujemy odcinek CF i uzyskujemy punkt G. Kąt AOG jest 3 razy mniejszy od kąta AOB.
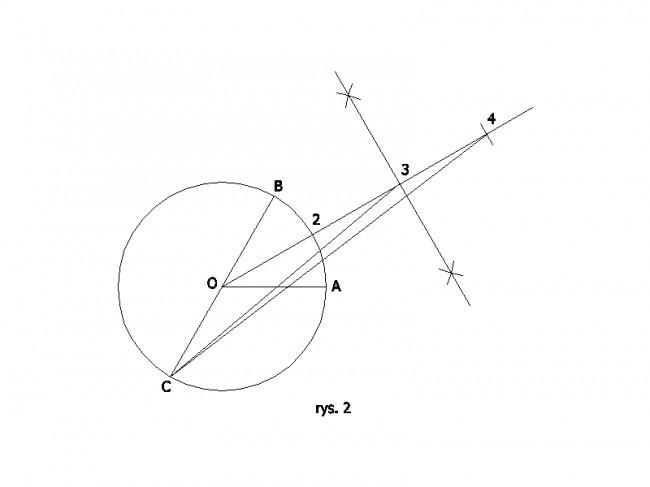
Aby wyznaczyć odpowiedni punkt na dwusiecznej danego kąta, należy ustalić ,w którym przedziale dwusiecznej ( na którym odcinku) będzie się on znajdował, ponieważ na dwusiecznej kąta można wyznaczyć przedziały (odcinki). Następnie wykonujemy symetralne odpowiednich odcinków, które wyznaczą nam szukane punkty. I tak pierwszy przedział to (2;4> i kończy się podziałem kąta na 4 równe części. W tym przedziale dany kąt AOB podzielimy na 3 i 4 części.(rys.2)
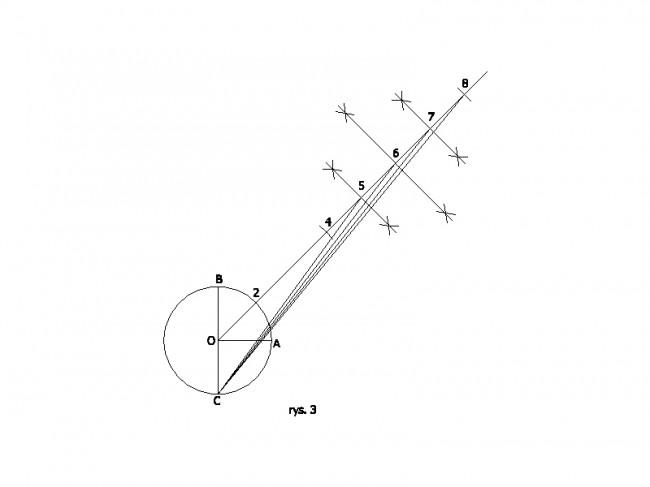
Drugi przedział to (4;8> i kończy się podziałem kąta na 8 równych części. W tym przedziale dany kąt AOB podzielimy na 5, 6, 7 i 8 części.(rys.3)
Trzeci przedział to (8;16> i kończy się podziałem kąta na 16 równych części. W tym przedziale dany kąt AOB podzielimy na 9, 10, 11, 12, 13, 14, 15 i 16 części. Takich przedziałów jest nieskończenie dużo.
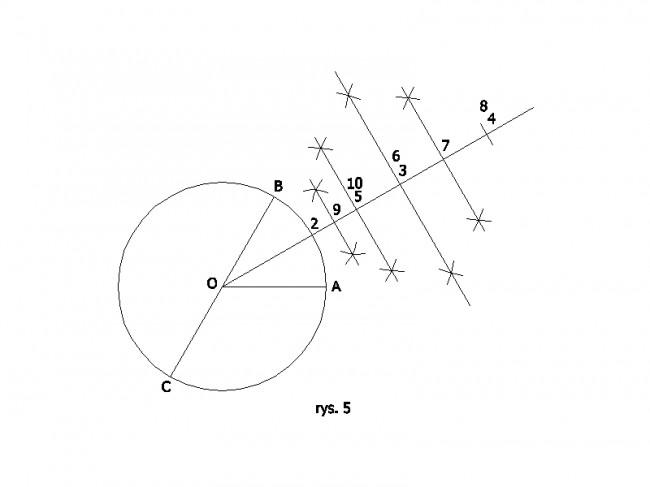
Ale możemy również w każdym z tych przedziałów podzielić dany kąt AOB na dowolną liczbę części, czyli np. w pierwszym przedziale (2;4> możemy podzielić dany kąt AOB na 3, 4, 5, 6, 7, 8, 9, itd. części (rys.5), lub w drugim przedziale (4;8> możemy podzielić dany kąt AOB na 3, 4, 5, 6, 7, 8, 9, itd. części. Im większy numer przedziału wybierzemy, tym z większą dokładnością po przecinku wykonamy podział danego kąta zakładając, że nasze narzędzia są idealnie precyzyjne. Dowolnie wybrany przedział (oprócz pierwszego) daje 4 razy dokładniejszy podział kąta na części od poprzedniego przedziału.
Należy równocześnie pamiętać, że dzieląc dany kąt AOB na dowolną liczbę części w wybranym przedziale trzeba ustalić czy otrzymane kąty będziemy jeszcze dzielić dwusiecznymi, pomnażać albo pozostawimy je bez zmian. Będzie to zależało od tego jaką część kąta chcemy uzyskać w danym przedziale. Na przykład dzieląc kąt AOB na 5 części w pierwszym przedziale (2;4>, należy otrzymany kąt AOH podzielić jeszcze na pół (pojedyncza dwusieczna), bo 5-ta część znajduje się w drugim przedziale, który jest wyżej o 1 przedział od przedziału pierwszego, a otrzymana połówka to 5-ta część kąta AOB.(rys.4)
Podział kąta na 5 części w pierwszym przedziale (2;4>
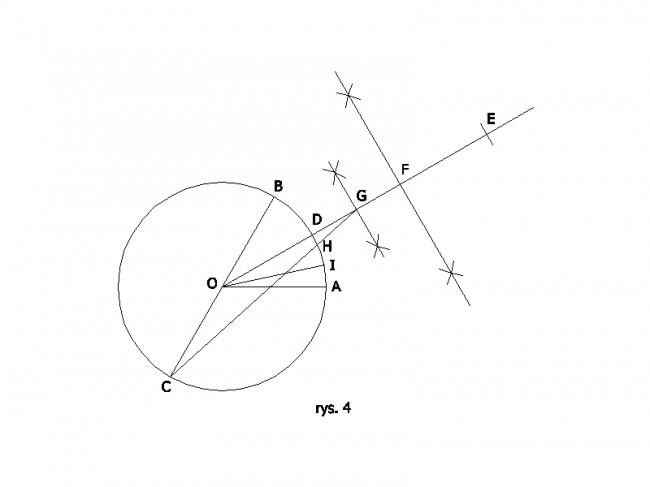
Opis czynności:
1. Rysujemy okrąg o środku O i promienu r oraz kąt środkowy AOB, gdzie r = OA = OB
2. Przedłużamy jedno z ramion kąta i punkt przecięcia się z okręgiem oznaczamy C
3. Kreślimy dwusieczną kąta AOB i otrzymujemy punkt D
4. Na dwusiecznej odkładamy odcinek DE = CD
5. Kreślimy symetralną odcinka DE i otrzymujemy punkt F
6. Kreślimy symetralną odcinka DF i otrzymujemy punkt G
7. Rysujemy odcinek CG i otrzymujemy punkt H
8. Dzielimy kąt AOH na pół i uzyskujemy punkt I. Kąt AOI jest 5 razy mniejszy od kąta AOB
Gdybyśmy chcieli dany kąt AOB podzielić na 9 części w pierwszym przedziale (2;4>, to otrzymany kąt należy podzielić na 4 równe części (podwójna dwusieczna), bo 9-ta część znajduje się w trzecim przedziale, który jest wyżej o 2 przedziały od przedziału pierwszego. Ale gdybyśmy chcieli ten sam kąt podzielić na 9 części w drugim przedziale, to otrzymany kąt należy podzielić tylko na pół (pojedyncza dwusieczna), bo 9-ta część znajduje się w trzecim przedziale, który jest wyżej o 1 przedział od przedziału drugiego. Czyli liczba dwusiecznych zależy od różnicy numeru przedziału, z którego pochodzi liczba części i numeru przedziału, w którym dokonujemy podziału danego kąta AOB. Taką różnice wykonujemy tylko wtedy gdy numer przedzaiłu, z którego pochodzi liczba części jest większy od numeru przedziału, w którym dokonujemy podziału danego kąta AOB.
Natomiast mnożymy otrzymane kąty, wtedy gdy numer przedziału, w którym dokonujemy podziału danego kąta AOB jest wyższy od numeru przedziału, z którego pochodzi liczba części na którą chcemy podzielić kąt AOB. Na przykład chcąc dokonać dokładniejszej trysekcji kąta AOB wybierając drugi przedział, należy otrzymany kąt zwiększyć dwukrotnie. Tak otrzymana trysekcja jest 4 razy dokładniejsza od trysekcji wykonanej w pierwszym przedziale. (rys.6)
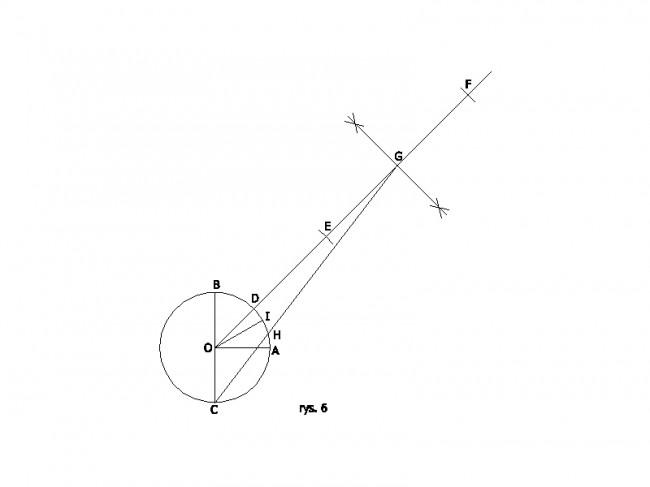
Opis czynności:
1. Rysujemy okrąg o środku O i promienu r oraz kąt środkowy AOB, gdzie r = OA = OB
2. Przedłużamy jedno z ramion kąta i punkt przecięcia się z okręgiem oznaczamy C
3. Kreślimy dwusieczną kąta AOB i otrzymujemy punkt D
4. Na dwusiecznej odkładamy odcinek DE = CD
5. Na dwusiecznej odkładamy odcinek EF = CE
6. Kreślimy symetralną odcinka EF i otrzymujemy punkt G
7. Łączymy punkty C i G odcinkiem i uzyskujemy punkt H
8. Kąt AOH zwiększamy 2 razy i otrzymujemy kąt AOI, który jest 3 razy mniejszy od kąta AOB
Jeśli chcemy otrzymać trysekcje 16 razy dokładniejszą od trysekcji z pierwszego przedziału, to wybierzmy trzeci przedział. Wtedy otrzymany kąt należy zwiększyć czterokrotnie.
Bez zmian pozostawiamy otrzymane kąty w wyniku podziału danego kąta AOB, gdy liczba części na którą dzielimy ten kąt należy do przedziału, w którym dokonujemy podziału.
Gdy potrafimy dzielić kąty z przedziału (0;180> na dowolną liczbę części, to bez problemu możemy skonstruować dowolny wielokąt foremny wpisany w okrąg. Np. aby uzyskać siedmiokąt foremny, należy podzielić kąt 90 stopni na 7 części, a następnie wybrać 4 kolejne części (bo 360 : 90 = 4), które utworzą bok szukanego siedmiokąta foremnego.
