Czy moje intuicje mają sens? Układają się w pewną logikę. W 4-D znajdują potwierdzenie, ale jak wyjść z 3-D?
POJĘCIE ALL-WEKTORA I JEGO INTERPRETACJA GEOMETRYCZNA W SFERZE 4-D
All-wektor to połączenie co najmniej 2 wektorów, które w sumie dają wektor zerowy w punkcie o współrzędnych (0,0). Takich All-wektorów może być nieskończenie wiele, ale może być również jeden i tylko jeden, który całkowicie wypełnia swoją złożonością płaszczyznę liczb zespolonych. Dlatego też warto poznać najprostszy model All-wektora, który można stworzyć przez dodanie 2 wektorów symetrycznych względem punktu (0,0), ale jednocześnie oba wektory muszą mieć tą samą wartość, lecz przeciwny kierunek. W tym ujęciu najprostszym przykładem all-wektora jest wektor i antywektor.
Na rysunku poniżej mamy przykład złożenia 2 wektorów w i -w, które razem tworzą wektor zerowy w punkcie (0,0).
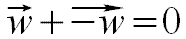
Takich najprostszych All-wektorów jesteśmy w stanie stworzyć nieskończenie wiele.
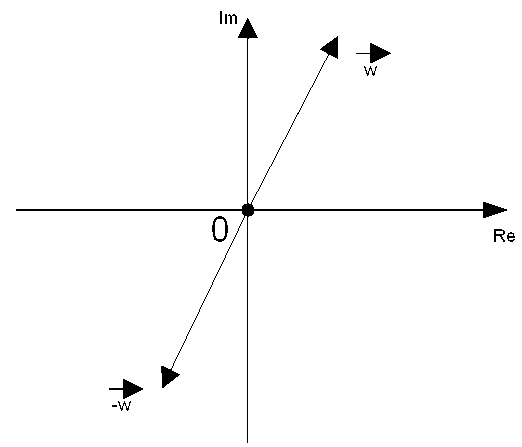
Wszystkie takie All-wektory zapełniają całą płaszczyzną zespoloną i tworzą ten jeden, jedyny All-wektor all, który jest sumą wszystkich All-wektorów.
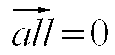
Takie szczególne All-wektory all możemy mnożyć i wynikiem takiego mnożenia jest struktura 4-wymiarowa o wartości 0.
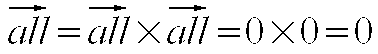
Wzory all-wektora
Ponieważ wszystkie All-wektory są równe 0, również przypadek szczególny all, to możemy zastosować prosty wzór, który przedstawia nam na płaszczyźnie punkt (0,0).
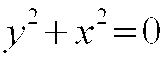
Rozważaliśmy wcześniej All-wektor all w strukturze 4-wymiarowej i dzięki temu doszliśmy do bardzo ciekawych wzorów:
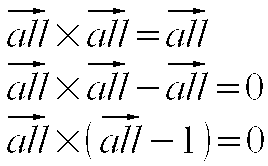
Jak widzimy struktury 4-wymiarowe, które powstają w wyniku wymnożenia 2 All-wektorów all, możemy przyrównać do 2-wymiarowego All-wektora all, który bierze udział w tym wymnażaniu, jako część składowa. Możemy tu zaobserwować dodatkową symetrię, która wcześniej była identyfikowana z zerem, a teraz dodatkowo z jedynką. Ta jedynka powstała dzięki znalezieniu części wspólnej obu struktur 2-D i 4-D i w wyniku jej działania, całość struktury jest nadal równa zero.
Ale to nie koniec naszych rozważań i wyliczeń. Możemy nasz wynik przyrównać z drugim All-wektorem all i pewnie znowu nas coś zaskoczy.
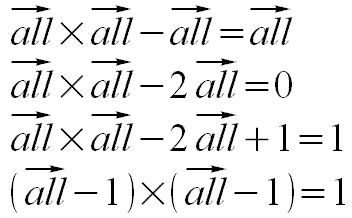
Zadziwiające, na początku mieliśmy tylko zero, a teraz, gdy cała sfera 4-D przeniknęła obie płaszczyzny, z których powstała, to uzyskaliśmy trzy jedynki i wynik z prawej strony równania przeszedł z 0 do 1.
Sfera 4-D jako cała struktura, przez przeniknięcie samej siebie, uzyskała nowe własności, które są identyfikowane dla nowej symetrii w jedynce. Coś co nie jest widoczne na pierwszy rzut oka, odsłania nam się po przeniknięciu wszystkich wymiarów i to jest novum!
Spróbujmy to samo osiągnąć dzięki zastosowaniu wzoru:
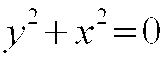 .
.
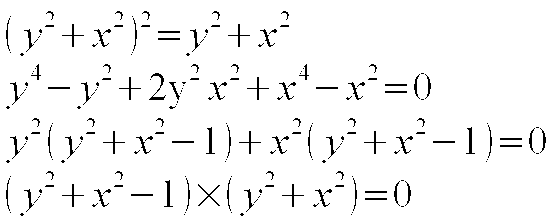
I teraz ostatni etap przyrównania struktur z zastosowaniem wzoru:
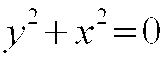 .
.
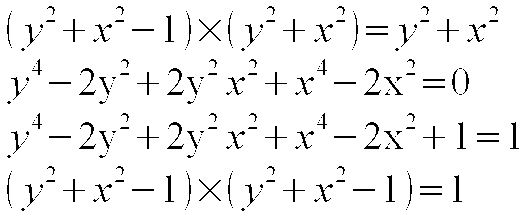
Jak widzimy, otrzymaliśmy to samo, choć trudniejszą drogą i powstał nam nowy wzór All-wektorowy, który znamy z wcześniejszych rozważań:
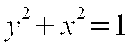 .
.
Jak pamiętamy, jest to wzór koła o promieniu r równym jeden.
Tajemniczy wzór znowu powrócił, a my widząc go, możemy tylko się uśmiechnąć :-), znowu.
Interpretacja geometryczna all-wektora
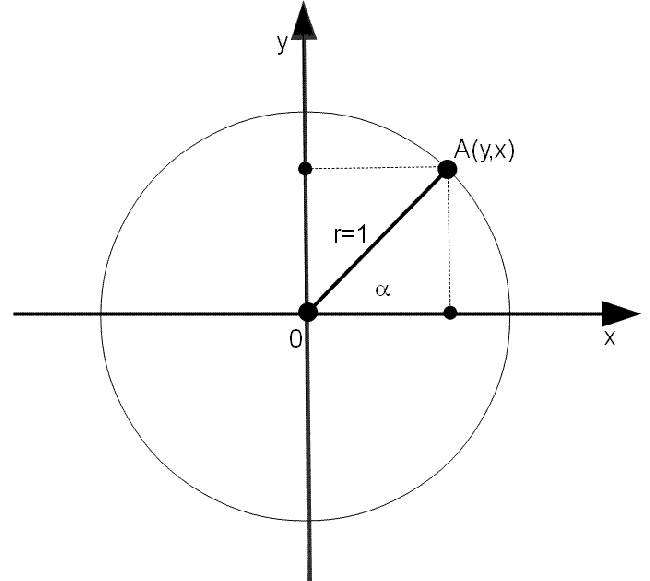
Możemy dojść do wniosku, na podstawie naszych dotychczasowych rozważań, że w sferze 4-D zachodzą zaskakujące zjawiska dla nas, gdyż swoją wyobraźnią sięgamy zaledwie do przestrzeni 3-D.
Jeżeli zero jest w 4-D, to samo przenikanie się struktur 2-D z całością prowadzi do nowej jakości, w postaci równania koła o promieniu równym jeden. Ale to jeszcze nie koniec. Istnieje przypuszczenie, tutaj potwierdzone wyliczeniami, że sfera 4-D funkcjonuje nie tylko dzięki 2 płaszczyznom 2-D, które ją tworzą, ale również dzięki jeszcze większym sferom, o większej ilości wymiarów. Może tu funkcjonować tak zwana matrioszka, która dziedziczy w dół pewne parametry dotyczące symetrii i ich struktur.
Jeżeli coś jest doskonałego w wyższych wymiarach, ma to zbawienny wpływ na niższe wymiary i jednocześnie sprawia, że te niższe wymiary mogą istnieć. Innymi słowy ma tu miejsce swoista harmonia między tym, co na górze z tym co na dole.
Ta harmonia ma strukturę wirową i wynika z przenikania się wymiarów nawzajem. Niestety nie możemy sobie wyobrazić sfery 4-D i jedynie płaszczyzna 2-D z drugą płaszczyzną 2-D daje nam jakieś wyobrażenie tego, co powstaje dzięki przenikaniu. Między jedną płaszczyzną 2-D, a sferą 4-D powstaje pierwszy okrąg o promieniu równym 1, również pomiędzy drugą płaszczyzną 2-D, a tą samą sferą 4-D powstaje drugi okrąg o promieniu równym 1, a trzecia struktura, a właściwie sfera o promieniu równym 1 powstaje wewnątrz struktury 4-D, jako element harmonii jeszcze większej struktury i rezonans struktur. Sfera 4-D drga wirowo jedynką i tworzy 2 wymnożone koła o promieniu r równym 1.
Teraz możemy narysować to schematycznie.
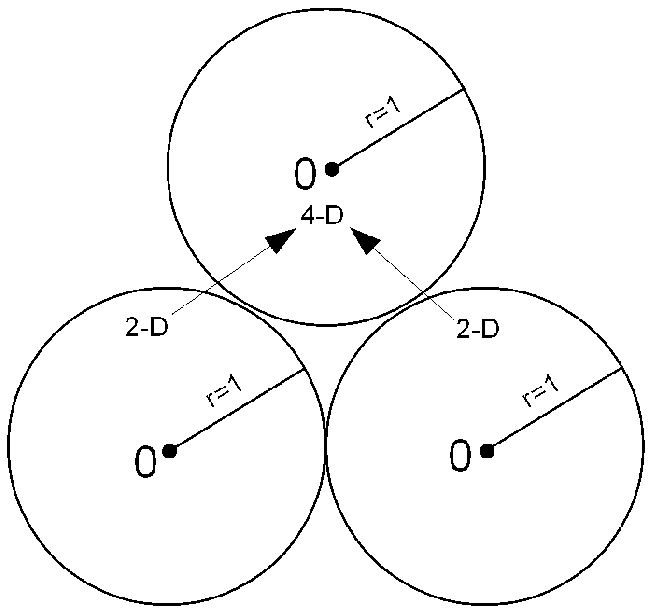
Niestety nie narysujemy sfery 4-D, dlatego możemy ją przedstawić tylko symbolicznie. Gdybyśmy narysowali kulę o promieniu r równym 1, zabrakłoby jednego wymiaru, bo kula jest obiektem 3-D. Ale za to możemy wyodrębnić 2 składowe tej sfery 4-D, czyli 2 okręgi o promieniu r równym 1. Niby nie wiele osiągnęliśmy, ale to jest i tak dużo, bo znamy wewnętrzną strukturę i o to tutaj nam chodziło. W zasadzie jest to ciekawe, ale jeszcze ciekawsze jest to, że owe 2 koła o promieniu r równym 1, wymnożone razem tworzą nieznaną nam strukturę, która jest zwiększona o jedynkę. To jest właśnie zaskakujące, że w 4-D powstaje dodatkowo wartość dodana równa jeden. Nie rozumiemy jeszcze skąd się bierze ta jedynka, bo nie znamy praw, które tym rządzą. W naszym świecie 3-D, jeżeli gdzieś oddajemy 1, to tą jedynkę w innym miejscu tracimy i bilans musi wyjść na 0. W 4-D tak nie jest i to nas zaskakuje. Oddanie 1 w jednym miejscu jednocześnie dodaje jedynkę w drugim miejscu i wygląda to jak rezonans, który działa na zasadzie, że równe przyciąga równe. Tak jakby jedynki z wyższych wymiarów przyciągały się.
C.D.N.

