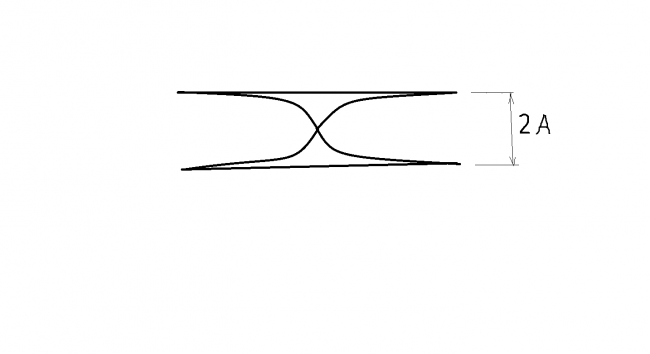edną z najodporniejszych na próby rozwikłania tajemnic przyrody jest masa elektronu która wynosi 0,510 998 9461(31) MeV/c²
Jedną z najodporniejszych na próby rozwikłania tajemnic przyrody jest masa elektronu która wynosi 0,510 998 9461(31) MeV/c² a właściwie ta tajemnica dotyczy wszystkich leptonów z Modelu Standardowego . W tym artykule przedstawię koncepcję wykorzystania Falowej teorii grawitacji do próby wyznaczenia mas leptonów. To przedsięwzięcie jest karkołomne zarówno ze względu na problemy pojęciowe (obszar w zasadzie nieznany nauce ) jak i trudności obliczeniowe powodowane złożonością zachodzących tam procesów. Konieczna jest tutaj wyobraźnia przestrzenna w 3D ( przydała by się animacja ale to poza moimi możliwościami) ale trzy wymiary i czas w zupełności wystarczają.
1, Model kwantu
Wyobraźmy sobie ruch obszaru przestrzeni składający się z n torusów o objętości Qn =2 π rn s, (przestrzeń torusów nie jest w jakikolwiek sposób wyróżniająca się od otoczenia z wyjątkiem jej ruchu ) gdzie promień rn =n lp, gdzie lp, to długość Planka a n liczby naturalne, natomiast s= Ip² to przekrój torusa. Ruch przestrzeni (torusa) realizuje się prostopadle do kierunku ruchu kwantu i jego obrotu (torus porusza w kierunku i wokół jego głównej osi), gdzie kinematyka polega na przekazywaniu „pędu” od torusa Qn do torusa Qn -1 do momentu osiągnięcia prędkości światła c, lub przeciwnym kierunku od prędkości c do minimalnej wartości V torusa o maksymalnym promieniu. W procesie tym zachowana jest zasada zachowania; iloraz prędkości i objętości torusa jest zawsze równy lp³c, gdzie c to prędkość światła. Czas ruchu pojedynczego torusa (w dowolnej chwili porusza się tylko jeden torus) jest równy czasowi Planka tp, co sprawia że ta złożona kinematyka w istocie przyjmuje formę fali. Po osiągnięciu prędkości światła c przestrzeń o objętości lp³ ulega całkowitej kontrakcji.
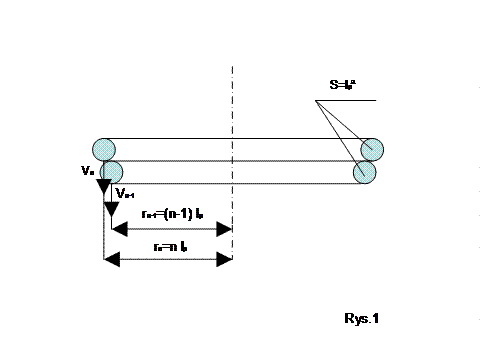
Vn Qn= c lp³
tn =tp
rn =n lp
λ =2 π r max =2 π lp n max
n max = λ / 2 π lp
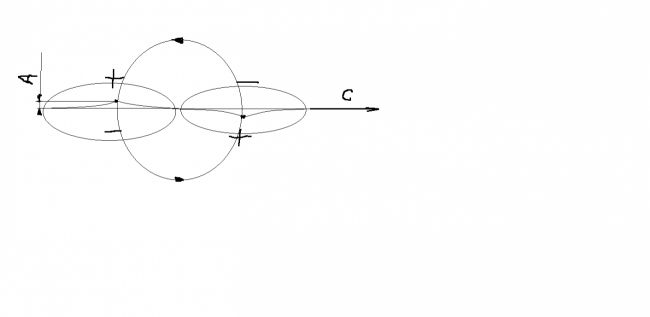
Kwant promieniowania elektromagnetycznego wyglądałby w dużym przybliżeniu, jak niżej..
Wektor C wskazuje kierunek propagacji kwantu a wielkość A amplitudę.. Ten prosty model zawiera w sobie trzy fundamentalne oddziaływania;
-elektryczne-ruch torusów prostopadle do kierunku propagacji
-magnetyczne-obrót wokół osi głównej torusa
-grawitacja –całkowita kontrakcja przestrzeni o objętości lp³ spowoduje powstanie rozprzestrzeniającej się kulistej fali kontrakcji. Obliczona stała sprzężenia α=10^-40 z tego modelu jest bliska uznanej. Ten model w zasadzie (funkcjonalnie) nie jest sprzeczne z równaniami Maxwella pomimo że znikają w nim sinusoidy.
2,Model leptonu- cząstki w istocie fundamentalnej.
W tych rozważaniach analizować będziemy cząstkę ( elektron) w absolutnym spoczynku ponieważ jakikolwiek jej ruch ten model straszliwie komplikuje W modelu cząstki analogicznie do kwantu, przestrzeń w postaci torusów wykonuje ruch równoległy do osi głównej oraz obrót przekazując „ pęd” zgodnie z prawem zachowania Vn Qn= c lp³ od prędkości c do prędkości V= c lp³ / Qmax co po prostych obliczeniach wyniesie V= lp c/ λ (analogia do równania Plancka nie jest przypadkowa) i ponownie do prędkości c i dalej po przeciwnej stronie ta sama kinematyka. Należy jeszcze raz podkreślić że w dowolnej chwili porusza się tylko jeden torus a więc te szkice mają charakter umowny. Bardzo uproszczony model cząstki wyglądał by jak poniżej.
3,Obliczmy parametry ruchu takiej cząstki ; amplitudę A oraz kąt φ
Vn Qn= c lp³
tn =tp
rn =n lp
λ =2 π r max =2 π lp n max
n max = λ / 2 π lp
Obliczenia amplitudy A
`Vn=An/tp = An c/lp gdzie An to długość ruchu entego torusa
Qn=2 π rn s=2 π lp³ n
Po podstawieniu An c/lp 2π lp³ n= c lp³
An=lp/2π 1/n
A= lp/2π Σ1/n – suma szeregu harmonicznego Σ1/n od n=1 do n= λ / 2 π lp
A= lp /2π ( ln (λ / 2 π lp) +γ) gdzie γ to stała Eulera równa 0,577 215.
Przyjmując długość fali Comptona dla elektronu 2, 426 ×10-12 m uzyskamy A=8,2928 lp. Ta wartość pozwala na obliczenie stałej struktury subtelnej.
Obliczenia kąta φ
Vn = ωn rn = φn/tp lp n= φn c n gdzie ωn prędkość kątowa entego torusa
Qn=2 π rn s=2 π lp³ n
φn c n 2 π lp³ n= c lp³
φn =1/2 π 1/n²
φ =1/2 π Σ 1/n² suma szeregu harmonicznego 1/n² od n=1 do n= λ / 2 π lp który dla elektronu jest rzędu 10^22 przyjmuję że dąży do nieskończoności ∞ wyniesie π ² / 6
φ =1/2 π π ² /6 = π/12
Ten kąt z oczywistych względów jest nieco mniejszy od 15 stopni i ma charakter unikalny dla danej cząstki.
4,Doszliśmy do momentu krytycznego to znaczy określenia warunku funkcjonowania takiej złożonej kinematyki. Wydaje mi się że aby ten byt trwał nieprzerwanie musimy połączyć dwa zdarzenia związkiem przyczynowo skutkowym a mianowicie; kontrakcję przestrzeni lp³ oraz nawrót ruchu torusa o obwodzie równym λ, a więc dwa skrajne zdarzenia. Kulista fala kontrakcji której długość L maleje z kwadratem odległości L= lp³ / 4 π r² porusza się po promieniu z prędkością światła c a torusy przekazując „ pęd ” tworzą krzywą logarytmiczną poruszając się też z prędkością światła c. Założenie jest następujące; tam gdzie te dwa różne zdarzenia się spotkają tam pojawi się lepton. Wydaje się że jest to absolutnie niemożliwe ponieważ droga logarytmiczna jest zdecydowanie dłuższa od drogi po promieniu i nie jest w stanie dogonić fali kontrakcji, ale tak jest gdy analizujemy te procesy przy użyciu czystej matematyki a te równania mają opisywać zdarzenia fizyczne.
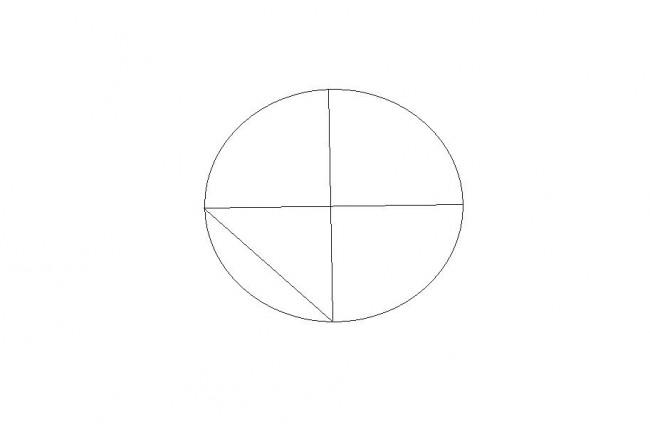
Prosty przykład na oszacowanie problemu. W okręgu rysujemy dwa promienie o długości r pod kątem prostym. Długość przeciwprostokątnej wyniesie √2 r, ≈1,414 r a długość łuku rozpiętego na promieniach π/2 r ≈ 1,571r. Z prostych obliczeń widać wyraźnie że łuk jest dłuższy o 0,157 r od prostej choć wizualnie wydaje się że ta różnica powinna być znacznie większa.
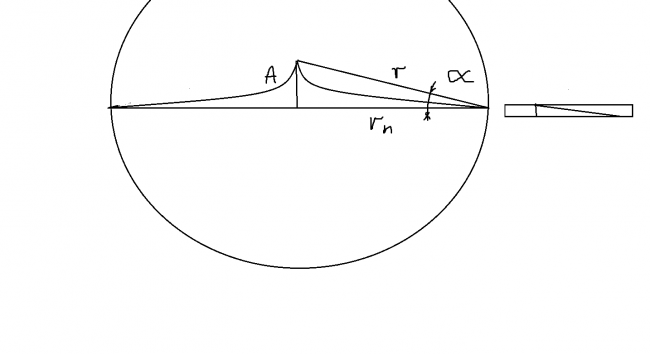
Wbrew pozorom różnica dróg logarytmicznej i prostej jest niewielka a po uwzględnieniu parametrów tych dróg oraz uwarunkowań fizycznych być może niemożliwe stanie się możliwe. Parametry tych dwóch zdarzeń;
rn =n lp
A=lp/2 π ( ln(n)+ γ)
r= (A²+rn ² )^0,5 = ((lp/2 π ( ln(n)+ γ) ² +n lp ²) ^0,5
sin α = A/r
Długość krzywej logarytmicznej L1 obliczymy z całki na długość łuku z funkcji f(x)= ln(x), gdzie liczby naturalne musimy zamienić na rzeczywiste (ta zamiana niesie pewne ryzyko);
L1 =∫ (1+[f´(x)] ²)^0,5 dx = ∫ (1+1/x²)0,5 dx
L1= ∫ ( x ² +1)^0,5/x dx = (x²+1)^0,5+ln|( x/((x²+1)^0,5+1) |
Warunek trwania cząstki;
L1=r – a
a-parametr - długość wynikająca z uwarunkowań fizycznych. Na wartość parametru a wpływać będą czynniki fizyczne np.;
-Promień przestrzeni ulegającej całkowitej kontrakcji ΔQ=lp³ o kształcie walca wyniesie
r= lp / √ π z artykułu Stała struktury subtelnej, którą prawdopodobnie należy odjąć od drogi fali kontrakcji.
- Fala kontrakcji dociera nie do abstrakcyjnego punktu tylko do przestrzeni o kształcie torusa o objętości Qn=2 π rn s=2 π lp³ n który porusza się z prędkością V= c/2 π n i ten fakt również skróci promień .
-Należy uwzględnić efekty relatywistyczne
-Pomiędzy zerem a jedynką liczb naturalnych oczywiście nie ma i ten fakt przy całkowaniu należy uwzględnić.
-Na pewno ta lista problemów do rozwiązania jest nie pełna i dlatego moje obliczenia mają charakter rozpoznawczy. Równanie po uproszczeniach miałoby postać jak niżej;
(x²+1)^0,5+ln|( x/((x²+1)^0,5+1) | = ( ( ln(n)+ γ) ² +n ²) ^0,5- a
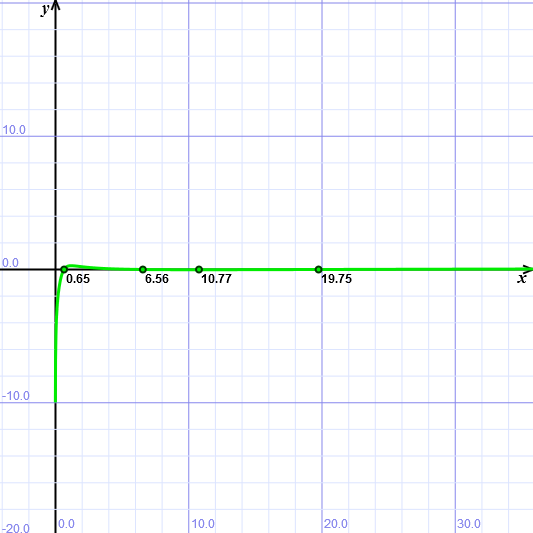
Równanie zamieniam na funkcję i przy pomocy programu do rysowania wykresów funkcji ze strony internetowej Matemaks szukam miejsc zerowych. Program ten mieści tylko 140 znaków .co wymusiło dokonanie kolejnych uproszczeń do postaci jak niżej;
(x²+1)^0,5+ln(| x/((x²+1)^0,5|) - ( ( ln(x)+0,5772) ² +x ²) ^0,5 -+a = y
Dla wartości a = 0,2 wykres przyjmuje dosyć ciekawą postać mianowicie pojawia się triplet miejsc zerowych (x=0,65 leży między zerem a jedynką) i choć do wartości nie należy przywiązywać większej wagi to jednak ten wynik może budzić pewne nadzieje.
Iwanowski Krzysztof
[i]