Poczynając od tego rozdziału przechodzimy do opisu algorytmów szybkich, tzn. takich, które posiadają klasę czasowej złożoności obliczeniowej równą O(n log n) lub nawet lepszą.
W informatyce zwykle obowiązuje zasada, iż prosty algorytm posiada dużą złożoność obliczeniową, natomiast algorytm zaawansowany posiada małą złożoność obliczeniową, ponieważ wykorzystuje on pewne własności, dzięki którym szybciej dochodzi do rozwiązania.
Wiele dobrych algorytmów sortujących korzysta z rekurencji, która powstaje wtedy, gdy do rozwiązania problemu algorytm wykorzystuje samego siebie ze zmienionym zestawem danych.
![]()
Jako przykład może posłużyć rekurencyjne obliczanie silni. Silnię liczby n należącej do zbioru liczb naturalnych definiujemy następująco:
n! = 1
2
3
...
(n - 1)
n
Na przykład: 5! = 1
2
3
4
5 = 120
Rekurencyjne obliczanie silni
Specyfikacja algorytmu
Dane wejściowe n - liczba, której silnie liczymy na danym poziomie rekurencyjnym, n N
Dane wyjściowe Wartość silni n! Lista kroków
krok 1: Jeśli n < 2, silnia(n) 1 i zakończ algorytm
krok 2: silnia(n) n
silnia(n - 1) i zakończ algorytm
Przykładowy program w języku Pascal
// Rekurencyjne obliczanie silni
//------------------------------
// (C)2005 mgr Jerzy Wałaszek
// I LO w Tarnowie
//------------------------------
program silnia_rek;
function silnia(n : integer) : extended;
begin
if n < 2 then silnia := 1 else silnia := n * silnia(n - 1);
end;
var
n : cardinal;
begin
writeln('Program oblicza rekurencyjnie silnie z liczby n');
writeln('-----------------------------------------------');
writeln('(C)2005 mgr Jerzy Walaszek I LO w Tarnowie');
writeln;
write('Podaj n = '); readln(n);
writeln;
writeln(n,'! = ',silnia(n):0:0);
writeln;
write('Nacisnij Enter...'); readln;
end.Dzięki rekurencji funkcja wyliczająca wartość silni staje się niezwykle prosta. Najpierw sprawdzamy warunek zakończenia rekurencji, tzn. sytuację, gdy wynik dla otrzymanego zestawu danych jest oczywisty. W przypadku silni sytuacja taka wystąpi dla n < 2 - silnia ma wartość 1. Jeśli warunek zakończania rekurencji nie wystąpi, to wartość wyznaczamy za pomocą rekurencyjnego wywołania obliczania silni dla argumentu zmniejszonego o 1. Wynik tego wywołania mnożymy przez n i zwracamy jako wartość silni dla n.
Wynaleziony w 1945 roku przez Johna von Neumanna algorytm sortowania przez scalanie jest algorytmem rekurencyjnym. Wykorzystuje zasadę dziel i zwyciężaj, która polega na podziale zadania głównego na zadania mniejsze dotąd, aż rozwiązanie stanie się oczywiste. Algorytm sortujący dzieli porządkowany zbiór na kolejne połowy dopóki taki podział jest możliwy (tzn. podzbiór zawiera co najmniej dwa elementy). Następnie uzyskane w ten sposób części zbioru rekurencyjnie sortuje tym samym algorytmem. Posortowane części łączy ze sobą za pomocą scalania tak, aby wynikowy zbiór był posortowany.
Scalanie zbiorów uporządkowanych
Podstawową operacją algorytmu jest scalanie dwóch zbiorów uporządkowanych w jeden zbiór również uporządkowany. Operację scalania realizujemy wykorzystując pomocniczy zbiór, w którym będziemy tymczasowo odkładać scalane elementy dwóch zbiorów. Ogólna zasada jest następująca:
Przygotuj pusty zbiór tymczasowy
Dopóki żaden ze scalanych zbiorów nie jest pusty, porównuj ze sobą pierwsze elementy każdego z nich i w zbiorze tymczasowym umieszczaj mniejszy z elementów usuwając go jednocześnie ze scalanego zbioru.
W zbiorze tymczasowym umieść zawartość tego scalanego zbioru, który zawiera jeszcze elementy.
Zawartość zbioru tymczasowego przepisz do zbioru wynikowego i zakończ algorytm.
Połączmy za pomocą opisanego algorytmu dwa uporządkowane zbiory: { 1 3 6 7 9 } z { 2 3 4 6 8 }
Scalane
zbioryZbiór
tymczasowyOpis wykonywanych działań [1] 3 6 7 9
2 3 4 6 8Porównujemy ze sobą najmniejsze elementy scalanych zbiorów. Ponieważ zbiory te są już uporządkowane, to najmniejszymi elementami będą zawsze ich pierwsze elementy.
2 3 4 6 8W zbiorze tymczasowym umieszczamy mniejszy element, w tym przypadku będzie to liczba 1. Jednocześnie element ten zostaje usunięty z pierwszego zbioru
[2] 3 4 6 81Porównujemy kolejne dwa elementy i mniejszy umieszczamy w zbiorze tymczasowym.
3 4 6 8Następne porównanie i w zbiorze tymczasowym umieszczamy liczbę 3. Ponieważ są to elementy równe, to nie ma znaczenia, z którego zbioru weźmiemy element 3.
[3] 4 6 8Teraz do zbioru tymczasowego trafi drugie 3.
[4] 6 8W zbiorze tymczasowym umieszczamy mniejszy z porównywanych elementów, czyli liczbę 4.
6 8Porównywane elementy są równe, zatem w zbiorze tymczasowym umieszczamy dowolny z nich.
[6] 8Teraz drugą liczbę 6.
8W zbiorze tymczasowym umieszczamy liczbę 7
[8]Teraz 8 Drugi zbiór jest pusty. Od tego momentu już nie porównujemy, lecz wprowadzamy do zbioru tymczasowego wszystkie pozostałe elementy pierwszego zbioru, w tym przypadku będzie to liczba 9. Koniec scalania. Zbiór tymczasowy zawiera wszystkie elementy scalanych zbiorów i jest uporządkowany. Możemy w dalszej kolejności przepisać jego zawartość do zbioru docelowego. Z podanego przykładu możemy wyciągnąć wniosek, iż operacja scalania dwóch uporządkowanych zbiorów jest dosyć prosta. Diabeł jak zwykle tkwi w szczegółach.
Algorytm scalania dwóch zbiorów
Przed przystąpieniem do wyjaśniania sposobu łączenia dwóch zbiorów uporządkowanych w jeden zbiór również uporządkowany musimy zastanowić się nad sposobem reprezentacji danych. Przyjmijmy, iż elementy zbioru będą przechowywane w jednej tablicy, którą oznaczymy literką d. Każdy element w tej tablicy będzie posiadał swój numer, czyli indeks z zakresu od 1 do n.
Kolejnym zagadnieniem jest sposób reprezentacji scalanych zbiorów. W przypadku algorytmu sortowania przez scalanie zawsze będą to dwie przyległe połówki zbioru, który został przez ten algorytm podzielony. Co więcej, wynik scalenia ma być umieszczony z powrotem w tym samym zbiorze.
![]()
Prześledźmy prosty przykład. Mamy posortować zbiór o postaci: { 6 5 4 1 3 7 9 2 }
Sortowany zbiór Opis wykonywanych operacji d[1] d[2] d[3] d[4] d[5] d[6] d[7] d[8] 6 5 4 1 3 7 9 2 Zbiór wyjściowy. 6 5 4 1 3 7 9 2 Pierwszy podział. 6 5 4 1 3 7 9 2 Drugi podział 6 5 4 1 3 7 9 2 Trzeci podział. 5 6 1 4 3 7 2 9 Pierwsze scalanie. 4 5 6 2 3 7 9 Drugie scalanie. 1 2 3 4 5 6 7 9 Trzecie scalanie. Koniec. Ponieważ w opisywanym tutaj algorytmie sortującym scalane podzbiory są przyległymi do siebie częściami innego zbioru, zatem logiczne będzie użycie do ich definicji indeksów wybranych elementów tych podzbiorów:
ip - indeks pierwszego elementu w młodszym podzbiorze is - indeks pierwszego elementu w starszym podzbiorze ik - indeks ostatniego elementu w starszym podzbiorze Przez podzbiór młodszy rozumiemy podzbiór zawierający elementy o indeksach mniejszych niż indeksy elementów w podzbiorze starszym.
pozostała część zbioru ip ... is ... ik pozostała część zbioru młodszy podzbiór
starszy podzbiór
Indeks końcowego elementu młodszej połówki zbioru z łatwością wyliczamy - będzie on o 1 mniejszy od indeksu pierwszego elementu starszej połówki.
![]()
Po pierwszym podziale prezentowanego powyżej zbioru otrzymujemy następujące wartości indeksów:
Młodsza
połówkaStarsza
połówkaip = 1 is = 5 ik = 8 Po kolejnym podziale połówek otrzymujemy 4 ćwiartki dwuelementowe. Wartości indeksów będą następujące:
Młodsza połówka Starsza połówka Młodsza
ćwiartkaStarsza
ćwiartkaMłodsza
ćwiartkaStarsza
ćwiartkaip = 1 is = 3 ip = 5 is = 7 ik = 4 ik = 8
Specyfikacja algorytmu scalania
Scalaj(ip, is, ik)
Dane wejściowe
d[ ] - scalany zbiór ip - indeks pierwszego elementu w młodszym podzbiorze, ip N
is - indeks pierwszego elementu w starszym podzbiorze, is N
ik - indeks ostatniego elementu w starszym podzbiorze, ik N
Dane wyjściowe
d[ ] - scalony zbiór Zmienne pomocnicze
p[ ] - zbiór pomocniczy, który zawiera tyle samo elementów, co zbiór d[ ]. i1 - indeks elementów w młodszej połówce zbioru d[ ], i1 N
i2 - indeks elementów w starszej połówce zbioru d[ ], i2 N
i - indeks elementów w zbiorze pomocniczym p[ ], i N
Lista kroków algorytmu scalania
krok 1: i1 ip; i2
is; i
ip
krok 2: Dla i = ip, ip + 1, ..., ik: wykonuj
jeśli (i1 = is)(i2
ik
d[i1] > d[i2]), to
p[i]d[i2]; i2
i2 + 1
inaczej
p[i]d[i1]; i1
i1 + 1
krok 3: Dla i = ip, ip + 1,...,ik: d[i] p[i]
krok 4: Zakończ algorytm
Schemat blokowy algorytmu scalania
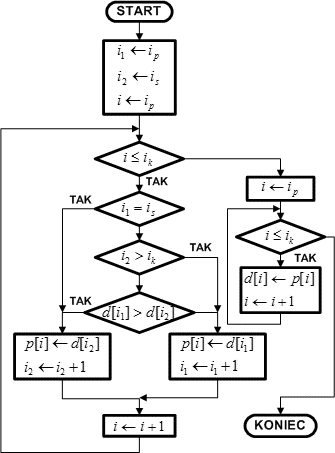
Operacja scalania dwóch podzbiorów wymaga dodatkowej pamięci o rozmiarze równym sumie rozmiarów scalanych podzbiorów. Dla prostoty na potrzeby naszego algorytmu zarezerwujemy tablicę p o rozmiarze równym rozmiarowi zbioru d[ ]. W tablicy p algorytm będzie tworzył zbiór tymczasowy, który po zakończeniu scalania zostanie przepisany do zbioru d[ ] w miejsce dwóch scalanych podzbiorów.
Parametrami wejściowymi do algorytmu są indeksy ip, is oraz ik, które jednoznacznie definiują położenie dwóch podzbiorów do scalenia w obrębie tablicy d[ ]. Elementy tych podzbiorów będą indeksowane za pomocą zmiennych i1 (młodszy podzbiór od pozycji ip do is - 1) oraz i2 (starszy podzbiór od pozycji is do ik). Na początku algorytmu przypisujemy tym zmiennym indeksy pierwszych elementów w każdym podzbiorze.
Zmienna i będzie zawierała indeksy elementów wstawianych do tablicy p[ ]. Dla ułatwienia indeksy te przebiegają wartości od ip do ik, co odpowiada obszarowi tablicy d[ ] zajętemu przez dwa scalane podzbiory. Na początku do zmiennej i wprowadzamy indeks pierwszego elementu w tym obszarze, czyli ip.
Wewnątrz pętli sprawdzamy, czy indeksy i1 i i2 wskazują elementy podzbiorów. Jeśli któryś z nich wyszedł poza dopuszczalny zakres, to dany podzbiór jest wyczerpany - w takim przypadku do tablicy p przepisujemy elementy drugiego podzbioru.
Jeśli żaden z podzbiorów nie jest wyczerpany, porównujemy kolejne elementy z tych podzbiorów wg indeksów i1 i i2. Do tablicy p[ ] zapisujemy zawsze mniejszy z porównywanych elementów. Zapewnia to uporządkowanie elementów w tworzonym zbiorze wynikowym. Po zapisie elementu w tablicy p[ ], odpowiedni indeks i1 lub i2 jest zwiększany o 1. Zwiększany jest również indeks i, aby kolejny zapisywany element w tablicy p[ ] trafił na następne wolne miejsce. Pętla jest kontynuowana aż do zapełnienia w tablicy p[ ] obszaru o indeksach od ip do ik.
Wtedy przechodzimy do końcowej pętli, która przepisuje ten obszar z tablicy p[ ] do tablicy wynikowej d[ ]. Scalane zbiory zostają zapisane zbiorem wynikowym, który jest posortowany rosnąco.
Specyfikacja algorytmu sortującego
Sortuj_przez_scalanie(ip, ik)
Dane wejściowe
d[ ] - sortowany zbiór ip - indeks pierwszego elementu w młodszym podzbiorze, ip N
ik - indeks ostatniego elementu w starszym podzbiorze, ik N
Dane wyjściowe
d[ ] - posortowany zbiór Zmienne pomocnicze
is - indeks pierwszego elementu w starszym podzbiorze, is N
Lista kroków algorytmu sortującego
krok 1: is (ip + ik + 1) div 2
krok 2: Jeśli is - ip > 1, to wywołaj rekurencyjnie Sortuj_przez_scalanie(ip, is - 1) krok 3: Jeśli ik - is > 0, to wywołaj rekurencyjnie Sortuj_przez_scalanie(is, ik) krok 4: Wywołaj Scalaj(ip, is, ik) i zakończ algorytm
Schemat blokowy algorytmu sortującego
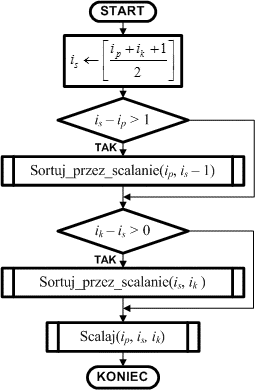
Algorytm sortowania przez scalanie jest algorytmem rekurencyjnym. Wywołuje się go z zadanymi wartościami indeksów ip oraz ik. Przy pierwszym wywołaniu indeksy te powinny objąć cały zbiór d, zatem ip = 1, a ik = n.
Najpierw algorytm wyznacza indeks is, który wykorzystywany jest do podziału zbioru na dwie połówki:
- młodszą o indeksach elementów od ip do is - 1
- starszą o indeksach elementów od is do ikNastępnie sprawdzamy, czy dana połówka zbioru zawiera więcej niż jeden element. Jeśli tak, to rekurencyjnie sortujemy ją tym samym algorytmem.
Po posortowaniu obu połówek zbioru scalamy je za pomocą opisanej wcześniej procedury scalania podzbiorów uporządkowanych i kończymy algorytm. Zbiór jest posortowany.
W przykładowych programach procedurę scalania umieściliśmy bezpośrednio w kodzie algorytmu sortującego, aby zaoszczędzić na wywoływaniu.
Poniższe, przykładowe programy są praktyczną realizacją omawianego w tym rozdziale algorytmu. Zapewne można je napisać bardziej efektywnie. To już twoje zadanie. Dokładny opis stosowanych środowisk programowania znajdziesz we wstępie. Programy przed opublikowaniem w serwisie edukacyjnym zostały dokładnie przetestowane. Jeśli jednak znajdziesz jakąś usterkę (co zawsze może się zdarzyć), to prześlij o niej informację do autora. Pozwoli to ulepszyć nasze artykuły. Będziemy Ci za to wdzięczni.
| Efekt uruchomienia programu |
|---|
 |
// Sortowanie Przez Scalanie
//-------------------------------------------------
// (C)2005 mgr Jerzy Wałaszek
// I Liceum Ogólnokształcące
// im. K. Brodzińskiego
// w Tarnowie
//-------------------------------------------------
program Merge_Sort;
const N = 20; // Liczebność zbioru.
var
d,p : array[1..N] of integer;
// Procedura sortująca
//--------------------
procedure MergeSort(i_p,i_k : integer);
var
i_s,i1,i2,i : integer;
begin
i_s := (i_p + i_k + 1) div 2;
if i_s - i_p > 1 then MergeSort(i_p, i_s - 1);
if i_k - i_s > 0 then MergeSort(i_s, i_k);
i1 := i_p; i2 := i_s;
for i := i_p to i_k do
if (i1 = i_s) or ((i2 <= i_k) and (d[i1] > d[i2])) then
begin
p[i] := d[i2]; inc(i2);
end
else
begin
p[i] := d[i1]; inc(i1);
end;
for i := i_p to i_k do d[i] := p[i];
end;
// Program główny
//---------------
var
i : integer;
begin
writeln(' Sortowanie przez scalanie ');
writeln('---------------------------');
writeln(' (C)2005 Jerzy Walaszek ');
writeln;
// Najpierw wypełniamy tablicę d[] liczbami pseudolosowymi
// a następnie wyświetlamy jej zawartość
randomize;
for i := 1 to N do d[i] := random(100);
writeln('Przed sortowaniem:'); writeln;
for i := 1 to N do write(d[i] : 4);
writeln;
// Sortujemy
MergeSort(1,N);
// Wyświetlamy wynik sortowania
writeln('Po sortowaniu:'); writeln;
for i := 1 to N do write(d[i] : 4);
writeln;
writeln('Nacisnij Enter...');
readln;
end.
// Sortowanie przez scalanie
//-------------------------------------------------
// (C)2005 mgr Jerzy Wałaszek
// I Liceum Ogólnokształcące
// im. K. Brodzińskiego
// w Tarnowie
//-------------------------------------------------
#include <cmath>
#include <iostream>
#include <iomanip>
using namespace std;
const int N = 20; // Liczebność zbioru.
int d[N],p[N];
// Procedura sortująca
//--------------------
void MergeSort(int i_p, int i_k)
{
int i_s,i1,i2,i;
i_s = (i_p + i_k + 1) / 2;
if(i_s - i_p > 1) MergeSort(i_p, i_s - 1);
if(i_k - i_s > 0) MergeSort(i_s, i_k);
i1 = i_p; i2 = i_s;
for(i = i_p; i <= i_k; i++)
p[i] = ((i1 == i_s) || ((i2 <= i_k) && (d[i1] > d[i2]))) ? d[i2++] : d[i1++];
for(i = i_p; i <= i_k; i++) d[i] = p[i];
}
// Program główny
//---------------
int main()
{
int i;
cout << " Sortowanie przez scalanie\n"
"---------------------------\n"
" (C)2005 Jerzy Walaszek\n\n"
"Przed sortowaniem:\n\n";
// Najpierw wypełniamy tablicę d[] liczbami pseudolosowymi
// a następnie wyświetlamy jej zawartość
srand((unsigned)time(NULL));
for(i = 0; i < N; i++) d[i] = rand() % 100;
for(i = 0; i < N; i++) cout << setw(4) << d[i];
cout << endl;
// Sortujemy
MergeSort(0,N-1);
// Wyświetlamy wynik sortowania
cout << "Po sortowaniu:\n\n";
for(i = 0; i < N; i++) cout << setw(4) << d[i];
cout << endl;
system("PAUSE"); return 0;
}
' Sortowanie Przez Scalanie
'-------------------------------------------------
' (C)2005 mgr Jerzy Wałaszek
' I Liceum Ogólnokształcące
' im. K. Brodzińskiego
' w Tarnowie
'-------------------------------------------------
OPTION EXPLICIT
CONST N = 20 ' Liczebność zbioru.
DIM SHARED d(1 TO N) AS INTEGER
DIM SHARED p(1 TO N) AS INTEGER
DECLARE SUB MergeSort(BYVAL i_p AS INTEGER, BYVAL i_k AS INTEGER)
DIM i AS INTEGER
PRINT " Sortowanie przez scalanie "
PRINT "---------------------------"
PRINT " (C)2005 Jerzy Walaszek "
' Najpierw wypełniamy tablicę d() liczbami pseudolosowymi
' a następnie wyświetlamy jej zawartość
RANDOMIZE TIMER
FOR i = 1 TO N: d(i) = INT(RND * 100): NEXT
PRINT "Przed sortowaniem:"
FOR i = 1 TO N: PRINT USING "####"; d(i);: NEXT
' Sortujemy
MergeSort 1, N
' Wyświetlamy wynik sortowania
PRINT "Po sortowaniu:"
FOR i = 1 TO N: PRINT USING "####"; d(i);: NEXT
PRINT "Nacisnij Enter..."
SLEEP
END
' Procedura sortująca
'--------------------
PUBLIC SUB MergeSort(BYVAL i_p AS INTEGER, BYVAL i_k AS INTEGER)
DIM i_s AS INTEGER, i1 AS INTEGER, i2 AS INTEGER, i AS INTEGER
i_s = INT((i_p + i_k + 1) / 2)
IF i_s - i_p > 1 THEN MergeSort i_p, i_s - 1
IF i_k - i_s > 0 THEN MergeSort i_s, i_k
i1 = i_p: i2 = i_s
FOR i = i_p TO i_k
IF (i1 = i_s) OR ((i2 <= i_k) AND (d(i1) > d(i2))) THEN
p(i) = d(i2): i2 = i2 + 1
ELSE
p(i) = d(i1): i1 = i1 + 1
END IF
NEXT
FOR i = i_p TO i_k: d(i) = p(i): NEXT
END SUB
<html>
<head>
</head>
<body>
<form style="BORDER-RIGHT: #ff9933 1px outset;
PADDING-RIGHT: 4px; BORDER-TOP: #ff9933 1px outset;
PADDING-LEFT: 4px; PADDING-BOTTOM: 1px;
BORDER-LEFT: #ff9933 1px outset; PADDING-TOP: 1px;
BORDER-BOTTOM: #ff9933 1px outset;
BACKGROUND-COLOR: #ffcc66" name="frmmergesort">
<h3 style="text-align: center">Sortowanie Przez Scalanie</h3>
<p style="TEXT-ALIGN: center">
(C)2005 mgr Jerzy Wałaszek - I LO w Tarnowie
</p>
<hr>
<p style="TEXT-ALIGN: center">
<input onclick="main()" type="button" value="Sortuj" name="B1">
</p>
<p id="t_out" style="TEXT-ALIGN: center">...</p>
</form>
<script language=javascript>
// Sortowanie Przez Scalanie
//-------------------------------------------------
// (C)2005 mgr Jerzy Wałaszek
// I Liceum Ogólnokształcące
// im. K. Brodzińskiego
// w Tarnowie
//-------------------------------------------------
var N = 20; // Liczebność zbioru.
var d = new Array(N);
var p = new Array(N);
// Procedura sortująca
//--------------------
function MergeSort(i_p, i_k)
{
var i_s,i1,i2,i;
i_s = Math.floor((i_p + i_k + 1) / 2);
if(i_s - i_p > 1) MergeSort(i_p, i_s - 1);
if(i_k - i_s > 0) MergeSort(i_s, i_k);
i1 = i_p; i2 = i_s;
for(i = i_p; i <= i_k; i++)
p[i] = ((i1 == i_s) || ((i2 <= i_k) && (d[i1] > d[i2]))) ? d[i2++] : d[i1++];
for(i = i_p; i <= i_k; i++) d[i] = p[i];
}
function main()
{
var i,t;
// Najpierw wypełniamy tablicę d[] liczbami pseudolosowymi
for(i = 0; i < N; i++) d[i] = Math.floor(Math.random() * 100);
t = "Przed sortowaniem:<BR><BR>";
for(i = 0; i < N; i++) t += d[i] + " ";
t += "<BR><BR>";
// Sortujemy
MergeSort(0,N-1);
// Wyświetlamy wynik sortowania
t += "Po sortowaniu:<BR><BR>";
for(i = 0; i < N; i++) t += d[i] + " ";
document.getElementById("t_out").innerHTML = t;
}
</script>
</body>
</html>
W celach badawczych testujemy czas wykonania algorytmu sortowania przez scalanie w środowisku opisanym we wstępie. Program testujący jest następujący:
// Program testujący czas sortowania dla
// danego algorytmu sortującego
//--------------------------------------
// (C)2005 mgr Jerzy Wałaszek
// I Liceum Ogólnokształcące
// w Tarnowie
//--------------------------------------
program TestCzasuSortowania;
uses Windows;
const
NAZWA = 'Sortowanie przez scalanie';
K1 = '----------------------------------------------------';
K2 = '(C)2005 mgr J.Wałaszek I LO w Tarnowie';
K3 = '------n---------tpo---------tod---------tpp---------tpk---------tnp';
K4 = '-------------------------------------------------------------------';
MAX_LN = 8; // określa ostatnie LN
LN : array[1..8] of integer = (1000,2000,4000,8000,16000,32000,64000,128000);
var
d,p : array[1..128000] of real; // sortowana tablica
n : integer; // liczba elementów
qpf,tqpc : int64; // dane dla pomiaru czasu
qpc1,qpc2 : int64;
// Tutaj umieszczamy procedurę sortującą tablicę d
//------------------------------------------------
procedure MergeSort(i_p,i_k : integer);
var
i_s,i1,i2,i : integer;
begin
i_s := (i_p + i_k + 1) div 2;
if i_s - i_p > 1 then MergeSort(i_p, i_s - 1);
if i_k - i_s > 0 then MergeSort(i_s, i_k);
i1 := i_p; i2 := i_s;
for i := i_p to i_k do
if (i1 = i_s) or ((i2 <= i_k) and (d[i1] > d[i2])) then
begin
p[i] := d[i2]; inc(i2);
end
else
begin
p[i] := d[i1]; inc(i1);
end;
for i := i_p to i_k do d[i] := p[i];
end;
function Sort : extended;
begin
QueryPerformanceCounter(addr(qpc1));
MergeSort(1,n);
QueryPerformanceCounter(addr(qpc2));
Sort := (qpc2 - qpc1 - tqpc) / qpf;
end;
// Program główny
//---------------
var
i,j,k : integer;
tpo,tod,tpp,tpk,tnp : extended;
f : Text;
begin
if QueryPerformanceFrequency(addr(qpf)) then
begin
QueryPerformanceCounter(addr(qpc1));
QueryPerformanceCounter(addr(qpc2));
tqpc := qpc2 - qpc1;
assignfile(f,'wyniki.txt'); rewrite(f);
// Wydruk na ekran
writeln('Nazwa: ',NAZWA);
writeln(K1);
writeln(K2);
writeln;
writeln(K3);
// Wydruk do pliku
writeln(f,'Nazwa: ',NAZWA);
writeln(f,K1);
writeln(f,K2);
writeln(f,'');
writeln(f,K3);
for i := 1 to MAX_LN do
begin
n := LN[i];
// Czas sortowania zbioru posortowanego
for j := 1 to n do d[j] := j;
tpo := Sort;
// Czas sortowania zbioru posortowanego odwrotnie
for j := 1 to n do d[j] := n - j;
tod := Sort;
// Czas sortowania zbioru posortowanego
// z przypadkowym elementem na początku - średnia z 10 obiegów
tpp := 0;
for j := 1 to 10 do
begin
for k := 1 to n do d[k] := k;
d[1] := random * n + 1;
tpp += Sort;
end;
tpp /= 10;
// Czas sortowania zbioru posortowanego
// z przypadkowym elementem na końcu - średnia z 10 obiegów
tpk := 0;
for j := 1 to 10 do
begin
for k := 1 to n do d[k] := k;
d[n] := random * n + 1;
tpk += Sort;
end;
tpk /= 10;
// Czas sortowania zbioru nieuporządkowanego - średnia z 10 obiegów
tnp := 0;
for j := 1 to 10 do
begin
for k := 1 to n do d[k] := random;
tnp += Sort;
end;
tnp /= 10;
writeln(n:7,tpo:12:6,tod:12:6,tpp:12:6,tpk:12:6,tnp:12:6);
writeln(f,n:7,tpo:12:6,tod:12:6,tpp:12:6,tpk:12:6,tnp:12:6);
end;
writeln(K4);
writeln(f,K4);
writeln(f,'Koniec');
closefile(f);
writeln;
writeln('Koniec. Wyniki w pliku WYNIKI.TXT');
end
else writeln('Na tym komputerze program testowy nie pracuje !');
writeln;
write('Nacisnij klawisz ENTER...'); readln;
end.Otrzymane wyniki są następujące (dla komputera o innych parametrach wyniki mogą się różnić co do wartości czasów wykonania, dlatego w celach porównawczych proponuję uruchomić podany program na komputerze czytelnika):
| Zawartość pliku wygenerowanego przez program | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Nazwa: Sortowanie przez scalanie Objaśnienia oznaczeń (wszystkie czasy podano w sekundach):
|
(Arkusz kalkulacyjny Excel do wyznaczania klasy czasowej złożoności obliczeniowej)
(Arkusz kalkulacyjny Excel do wyznaczania wzrostu prędkości sortowania)
Analizując wyniki obliczeń w arkuszu kalkulacyjnym otrzymanych czasów sortowania dla algorytmu sortowania przez scalanie wyciągamy następujące wnioski:
| Cechy Algorytmu Sortowania Przez Scalanie | |
|---|---|
| klasa złożoności obliczeniowej optymistyczna | O(n log n) |
| klasa złożoności obliczeniowej typowa | |
| klasa złożoności obliczeniowej pesymistyczna | |
| Sortowanie w miejscu | NIE |
| Stabilność | TAK |
Klasy złożoności obliczeniowej szacujemy następująco:
- optymistyczna - dla zbiorów uporządkowanych (z niewielką liczbą elementów nie na swoich miejscach) - na podstawie czasów tpo, tpp, tpk
- typowa - dla zbiorów o losowym rozkładzie elementów - na podstawie czasu tnp
- pesymistyczna - dla zbiorów posortowanych odwrotnie - na podstawie czasu tod.
| Własności algorytmu | ||||||||
|---|---|---|---|---|---|---|---|---|
| Algorytm | tpo | tod | tpp | tpk | tnp | |||
| Sortowanie przez scalanie | O(n log n) | O(n log n) | O(n log n) | O(n log n) | O(n log n) | |||
| tpo | tpp |
| ||||||
- Wszystkie badane czasy są proporcjonalne do nlog2n, zatem wnioskujemy, iż algorytm sortowania przez scalanie posiada klasę czasowej złożoności obliczeniowej równą O(n log n).
- Najdłużej trwa sortowanie zbioru nieuporządkowanego. Jednakże badane czasy nie różnią się wiele pomiędzy sobą, co sugeruje, iż algorytm nie jest specjalnie czuły na rozkład danych wejściowych.
| Wzrost prędkości sortowania | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorytmy | tpo | tod | tpp | tpk | tnp | ||||||||||||||
| Sortowanie metodą Shella Sortowanie przez scalanie |
|
|
|
|
| ||||||||||||||
| dobrze | dobrze | dobrze | dobrze | dobrze | |||||||||||||||
Porównanie czasów działania algorytmów sortowania metodą Shella oraz sortowania przez scalanie doprowadza do wniosku, iż ten drugi algorytm jest szybszy. W przypadku ogólnym zbiór zostanie posortowany 2,5 razy szybciej (dokładniejsza analiza na pewno pokaże, iż nie są to stosunki stałe, lecz zależą on liczby elementów w sortowanym zbiorze i rosną wraz ze wzrostem n). W przypadku zbioru posortowanego odwrotnie zysk jest dwukrotny. Szybkość działania jest jednak okupiona większym zapotrzebowaniem na pamięć - złożoność pamięciowa jest klasy O(n), gdyż dla n elementowego zbioru musimy dodatkowo zarezerwować tablicę n elementową dla zbioru będącego wynikiem scalania.
Porównaj wzrost prędkości działania algorytmu sortowania przez scalanie w stosunku do algorytmu sortowania przez wstawianie. Wyciągnij odpowiednie wnioski.
Ile razy zostanie podzielony zbiór 128 elementowy w trakcie działania algorytmu sortowania przez scalanie?
Podany algorytm scalania podzbiorów uporządkowanych można ulepszyć, jeśli rozważymy przypadki wyczerpania elementów w jednym z podzbiorów. Wtedy elementy drugiego podzbioru można bezpośrednio przekopiować do zbioru tymczasowego bez wykonywania dalszych porównań. Zaprojektuj taki algorytm, ułóż na jego podstawie program i sprawdź, czy to usprawnienie daje spodziewane przyspieszenie sortowania zbioru.
Określ klasę złożoności obliczeniowej operacji scalania dwóch zbiorów uporządkowanych m- i n elementowych.
Jak należy scalać podzbiory w algorytmie sortowania przez scalanie, aby był zachowany warunek stabilności - elementy równe zachowują swoją kolejność w zbiorze posortowanym.
Dokument ten rozpowszechniany jest zgodnie z zasadami licencji
GNU Free Documentation License.
Źródło: mgr Jerzy Wałaszek

