Sortowanie przez kopcowanie

Wprowadzenie

Kolejnym algorytmem sortowania jest sortowanie przez kopcowanie. Łączy on w sobie dwie wymagane od algorytmów cechy: jest szybki i mało "pamięciożerny". Jego czas działania wynosi O(n lg n) natomiast liczba elementów przechowywanych poza tablicą podczas całego procesu sortowania jest niezmienna. Aby jednak zrozumieć samo sortowanie przez kopcowanie, trzeba najpierw poznać strukturę danych, jaką jest sam kopiec.

Kopiec

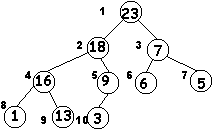Kopiec jest to tablica danych, która da się przedstawić graficznie w postaci drzewa binarnego. Każdy węzeł tego drzewa odpowiada jednemu elementowi tablicy (numery węzłów na rysunku oznaczone są liczbami po lewej stronie węzła). Tak więc dziesiąty element sortowanej tablicy nazwiemy węzłem numer 10. Dla każdego elementu możemy łatwo obliczyć jego "rodzica" (czyli na naszym rysunku jest to element "wyższy" od danego i z nim związany), oraz jego "liście": prawy i lewy. Numer rodzica jest obliczany według wzoru: numer rodzica = bieżący element / 2 (dzielenie bez reszty). Bieżący element jest elementem, dla którego liczymy numer rodzica. Tak więc rodzicem dla węzła 5 jest węzeł 2, gdyż 5/2=2. Tylko dla jednego węzła nie możemy policzyć rodzica: dla węzła pierwszego.

Numer lewego liścia, jak można zauważyć spoglądając na rysunek jest równie łatwy do obliczenia: lewy = bieżący x 2.

Ostatni wzór jest już chyba oczywisty: prawy = bieżący x 2 + 1.

Podczas korzystania z kopca polecam utworzyć funkcje, do których przekazujemy numer bieżącego elementu, a które zwracać nam będą numery tychże węzłów.

Kolejna, niezwykle istotna cecha kopca brzmi następująco: każdy węzeł przechowuje wartość nie mniejszą niż jego prawy i lewy "podwęzeł".

Radzę się przyjrzeć teraz rysunkowi i dobrze go przeanalizować. Zacznijmy od węzła pierwszego. Przechowuje on wartość 23. Wartości w węzłach niższych są mniejsze od 23, bowiem są to liczby 18 i 7. Spośród węzłów 2,4 i 5 największa jest dwójka, spośród 3,6 i 7 - trójka itd.

Przetwórzmy teraz rozrysowany kopiec na zwykłą tablicę. Pamiętać przy tym należy iż numer węzła jest pozycją, na jakiej dana wartość znajduje się w tablicy. Lecimy więc po kolei:

I to jest nasz kopiec w postaci tablicy.

W tej postaci bardziej widoczna staje się konieczność posiadania funkcji obliczającej numer lewego i prawego potomka oraz węzeł rodzica.

Proponuję dla poćwiczenia policzyć sobie dla paru przykładów takie węzły. Jaki jest na przykład numer rodzica elementu siódmego? Jakie są numery elementów "podrzędnych" wobec węzła czwartego ?

Takie ćwiczenia pozwolą "oswoić się" z strukturą kopca.

Tworzenie kopca z nieposortowanej tablicy

Teraz zajmijmy się utworzeniem kopca z pewnej tablicy, którą posiadamy w pamięci komputera.

Potrzebne nam w tej chwili będą dwie procedury oraz jedna zmienna, w której będziemy przechowywali wielkość kopca (rozmiar).

Wartość zmiennej rozmiar musimy mieć obliczoną przed wywołaniem procedury podanej poniżej. Zmienna rozmiar określa, ile elementów w tablicy należy do kopca. Kiedy np. wpiszemy do tablicy 10 liczb, ustawiamy tę zmienną na 10.

Jedna z procedur (nazwijmy ją uporządkuj_węzeł) ma następujący schemat:

główny - numer węzła do uporządkowania

l - zmienna do przechowywania numeru lewego węzła

p - zmienna do przechowywania numeru prawego węzła

największy - zmienna przechowująca numer największego el

oznaczenia:

<= - mniejszy lub równy

>= - większy lub równy

uporządkuj_węzeł (główny)

oblicz l // tutaj przydaje się funkcja o której była wcześniej mowa

oblicz p // j.w.

jeżeli (l <= rozmiar) oraz (wartość węzła l > wartość węzła główny) wtedy

największy = l

jeśli nie, największy = główny

jeżeli (p<= rozmiar) oraz (wartość węzła p > wartość węzła największego) wtedy

największy = p

jeżeli największy jest różny od główny wtedy:

1. zamień miejscami węzły o numerach największy oraz główny

2. wywołaj procedurę z parametrem największy (uporządkuj_węzeł (największy))

Zaznaczam jeszcze raz, że wartość węzła o numerze x to nic innego, jak wartość przechowywana w tablicy na pozycji x.

To była pierwsza potrzebna nam procedura. Jej znaczenie jest bardzo ważne - jest ona wywoływana praktycznie przy każdej operacji na kopcu, która narusza jego strukturę. Służy przede wszystkim do "zaprowadzenia porządku" czyli pilnuje, aby element "wyższy" nie był mniejszy od elementu "niższego".

Niestety, jednokrotne uruchomienie tej procedury z parametrem 1 ("korzeń" kopca) nie powoduje utworzenia z tablicy poprawnego kopca. Procedurą tą trzeba "potraktować każdy węzeł z osobna. No, może nie każdy. Bezcelowe bowiem byłoby uruchamianie tej procedury dla węzłów, które nie mają już swoich potomków. Po co bowiem sprawdzać, czy czasem potomek nie jest większy od rodzica, jeżeli rodzic NIE MA potomków ? :)

W kopcu zawsze jest tak, że połowa elementów (rozmiar/2 - dzielenie bez reszty) ma potomków, a cała reszta węzłów to "liście" drzewa - cierpią one na brak potomstwa ;) Naszą procedurę zatem wywołujemy tylko dla połowy elementów. Jednak pojawia się znów pytanie. Procedurę uporządkuj_węzeł wywołujemy począwszy od węzła pierwszego w dół, czy od połowy tablicy do jedynki ?

Odpowiedź wydaje się oczywista, kiedy zauważymy, że wywołanie naszej procedury powoduje "wydostanie się" największego spośród trzech elementów na szczyt naszej rójki. Jeżeli chodzi nam o to, by ten największy element znalazł się na samej górze, powinniśmy go "wyganiać" z góry do dołu, tak więc ostatecznie możemy stwierdzić, że procedura tworząca kopiec z naszej tablicy powinna wyglądać następująco:

Dla "bieżący" z przedziału malejącego od rozmiar/2 do 1

uporządkuj_węzeł(bieżący)

Przetłumaczenie tak prostej pętli na konkretny język programowania nikomu trudności sprawić nie powinno.

SORTOWANIE

Poznaliśmy już sposób, jak utworzyć sam kopiec z tablicy. Czynność ta powinna być niejako "wstępem" do samego sortowania przez kopcowanie (choć może "wstęp" tu nie pasuje, bo utworzenie kopca z tablicy to już 75 % sukcesu). Zakładając więc, że nasza tablica, którą mamy posortować ma już postać kopca, możemy przystąpić do prawidłowego sortowania (wreszcie, prawda ? :).

W tym momencie niezbędna nam będzie używana już wcześniej zmienna rozmiar, oznaczają rozmiar samego kopca, który będzie się "kurczył", aż zupełnie "zniknie", co będzie oznaczało koniec sortowania.

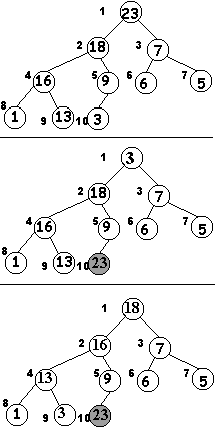Sam proces sortowania, jeżeli zrozumiałe jest dla nas wszystko co było opisane powyżej, jest już banalny. W kopcu pierwszy węzeł jest elementem największym, tak? Gdzie powinien się więc znaleźć największy węzeł ? Na końcu (posortowanej) tablicy. Zamieniamy zatem ostatni węzeł z pierwszym, węzeł ostatni "odcinamy" od kopca (poprzez zmniejszenie zmiennej rozmiar) i wywołujemy procedurę uporządkuj_węzeł dla węzła nr 1. W efekcie w tablicy będziemy mieli nieco mniejszy kopiec, a ostatni element tablicy (nie należący już do kopca) będzie miał wartość najwyższą z wszystkich elementów tablicy. Pokazane jest to na rysunku obok. Część pierwsza rysunku to nasz kopiec. Niżej widzimy element 1 zamieniony z elementem ostatnim oraz "obcięcie" kopca, poprzez zmniejszenie wartości zmiennej rozmiar. Trzecia część rysunku to sytuacja po uruchomieniu procedury uporządkuj_węzeł (1).

Wynik jest ciekawy, czynność zatem powtórzymy...

Zamiana węzła pierwszego z ostatnim, "obcięcie" kopca, uporządkuj_węzeł (1). Kopiec znowu zmalał, a dwa ostatnie elementy są już posortowane. Jeżeli czynność powtórzymy dostateczną ilość razy, kopiec zupełnie "zniknie" a tablica będzie już posortowana

Sama procedura sortująca ma więc postać:

Dla A z przedziału malejącego od ROZMIAR do 2:

Zamień węzeł A z węzłem ROZMIAR

Zmniejsz wartość zmiennej ROZMIAR

Uporządkuj_węzeł (1)