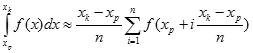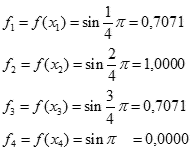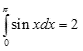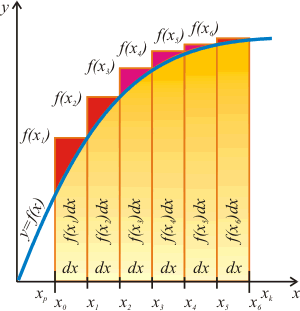
W metodzie prostokątów korzystamy z definicji całki oznaczonej Riemanna , w której wartość całki interpretowana jest jako suma pól obszarów pod wykresem krzywej w zadanym przedziale całkowania <xp,xk>. Sumę tę przybliżamy przy pomocy sumy pól odpowiednio dobranych prostokątów. Sposób postępowania jest następujący:
Przedział całkowania <xp,xk> dzielimy na n równo odległych punktów x1,x2,...,xn. Punkty te wyznaczamy w prosty sposób wg wzoru:
dla i = 1,2,...,n
Obliczamy odległość między dwoma sąsiednimi punktami - będzie to podstawa każdego prostokąta:
Dla każdego wyznaczonego w ten sposób punktu obliczamy wartość funkcji f(x) w tym punkcie:
fi = f(xi), dla i = 1,2,...,n
Obliczamy sumę iloczynów wyznaczonych wartości funkcji przez odległość dx między dwoma sąsiednimi punktami - da to sumę pól poszczególnych prostokątów ograniczonych wykresem funkcji:
S = f1 dx + f2 dx + ... + fn dx
a po wyprowadzeniu wspólnego czynnika przed nawias:
S = dx (f1 + f2 + ... + fn)
Otrzymana suma jest przybliżoną wartością całki oznaczonej funkcji f(x) w przedziale <xp,xk>.

Obliczymy ręcznie przybliżoną wartość całki oznaczonej z funkcji f(x) = sin(x) w przedziale <0,π>.
Przedział podzielimy na n = 4 punkty:
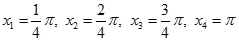
Odległość między dwoma sąsiednimi punktami wynosi:
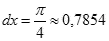
Dla każdego z wyznaczonych punktów obliczamy wartość funkcji f(x) = sin(x):
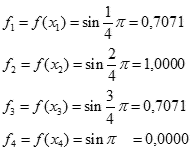
Obliczamy sumę pól prostokątów:
S = dx (f1 + f2 + f3 + f4)
S = 0,7854 (0,7071 + 1,000 + 0,7071 + 0,0000)
S = 0,7854  2,4142
2,4142
S = 1,8961
Dokładna wartość takiej całki oznaczonej wynosi wg tablic:
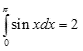
Zatem popełniliśmy błąd równy: 2 - 1,8961 = 0,1039, co stanowi nieco ponad 5% wartości dokładnej. W sumie nie jest to zły wynik zważywszy na ilość wykonanych przez nas rachunków. Jeśli chcemy zwiększyć dokładność, to musimy zsumować więcej prostokątów, ale to zostawimy już komputerom.

Dane wejściowe
| xp | - | początek przedziału całkowania, xp  R R |
| xk | - | koniec przedziału całkowania, xk  R R |
| n | - | liczba punktów podziałowych, n  N N |
| f(x) | - | funkcja rzeczywista, której całkę liczymy |
Dane wyjściowe
Wartość całki oznaczonej funkcji f(x) w przedziale <xp,xk>. Wynik jest liczbą rzeczywistą.
Zmienne pomocnicze
| s | - | suma wysokości prostokątów, którą później zamieniamy w wartość całki, s  R R |
| dx | - | odległość między dwoma sąsiednimi punktami podziałowymi, dx  R R |
| i | - | licznik punktów podziałowych, i  N N |

| krok 1: | Czytaj xp xk |
| krok 2: | s  0 0 |
| krok 3: | dx  | xk - xp | | n | |
| krok 4: | Dla i = 1,2,...,n, s  s + f(xp + i s + f(xp + i  dx) dx) |
| krok 5: | s  s s  dx dx |
| krok 6: | Pisz s i zakończ algorytm |

Po odczytaniu informacji o krańcach xp i xk przedziału całkowania ustawiamy sumę s na 0, obliczamy odległość dx pomiędzy sąsiednimi punktami podziałowymi i ustawiamy ich licznik na 1.
Rozpoczynamy pętlę iteracyjną, która wykona się n-razy. Wewnątrz pętli obliczamy i-ty punkt podziałowy oraz wartość funkcji w tym punkcie, którą dodajemy do sumy s.
Po zakończeniu pętli sumę s musimy jeszcze pomnożyć przez szerokość podstawy prostokątów, czyli odległość dx Po tej operacji s zawiera wartość przybliżoną całki. Zwracamy ją użytkownikowi i kończymy algorytm.

 | | |
| | |
| | | 
Poniższe, przykładowe programy są praktyczną realizacją omawianego w tym rozdziale algorytmu. Zapewne można je napisać bardziej efektywnie. To już twoje zadanie. Dokładny opis stosowanych środowisk programowania znajdziesz we wstępie. Programy przed opublikowaniem w serwisie edukacyjnym zostały dokładnie przetestowane. Jeśli jednak znajdziesz jakąś usterkę (co zawsze może się zdarzyć), to prześlij o niej informację do autora. Pozwoli to ulepszyć nasze artykuły. Będziemy Ci za to wdzięczni. | |
| | | | |
Prezentowane poniżej programy wyliczają całkę oznaczoną funkcji f(x) = x2 + 2x. Przedział całkowania jest dzielony na n=1000 punktów. W przedziale <0,1> całka oznaczona ma wartość dokładną równą 4/3 = 1.3333...
| Wydruk z uruchomionego programu |
Obliczanie całki oznaczonej
za pomocą metody prostokątów
----------------------------
(C)2006 mgr J.Wałaszek I LO
f(x) = x * x + 2 * x
Podaj początek przedziału całkowania
xp = 0
Podaj koniec przedziału całkowania
xk = 1
Wartość całki wynosi : 1,335
KONIEC. Naciśnij dowolny klawisz... |
| Microsoft Visual Basic 2005 Express Edition |
Borland
Delphi 7.0
Personal
Edition | //****************************************************
//** Obliczanie całki oznaczonej metodą prostokątów **
//** ---------------------------------------------- **
//** (C)2004 mgr Jerzy Wałaszek I LO w Tarnowie **
//****************************************************
program int_rect;
{$APPTYPE CONSOLE}
//*******************************
//** Tutaj definiujemy funkcję **
//*******************************
function f(x : real) : real;
begin
f := x * x + 2 * x;
end;
//********************
//** Program główny **
//********************
const N = 1000; //liczba punktów/prostokątów podziałowych
var
xp,xk,s,dx : real;
i : integer;
begin
writeln('Obliczanie calki oznaczonej');
writeln('za pomoca metody prostokatow');
writeln('----------------------------');
writeln('(C)2004 mgr J.Walaszek I LO');
writeln;
writeln('f(x) = x * x + 2 * x');
writeln;
writeln('Podaj poczatek przedzialu calkowania');
writeln;
write('xp = '); readln(xp);
writeln;
writeln('Podaj koniec przedzialu calkowania');
writeln;
write('xk = '); readln(xk);
writeln;
s := 0;
dx := (xk - xp) / N;
for i := 1 to N do s := s + f(xp + i * dx);
s := s * dx;
writeln('Wartosc calki wynosi : ',s:8:3);
writeln;
writeln('Nacisnij klawisz Enter...');
readln;
end. |
Borland
C++ Builder
6.0
Personal
Edition | //****************************************************
//** Obliczanie całki oznaczonej metodą prostokątów **
//** ---------------------------------------------- **
//** (C)2004 mgr Jerzy Wałaszek I LO w Tarnowie **
//****************************************************
#include <iomanip>
#include <iostream>
using namespace std;
//*******************************
//** Tutaj definiujemy funkcję **
//*******************************
double f(double x)
{
return(x * x + 2 * x);
}
//********************
//** Program główny **
//********************
main()
{
const int N = 1000; //liczba punktów/prostokątów podziałowych
double xp,xk,s,dx;
int i;
char c[1];
cout.precision(3); // 3 cyfry po przecinku
cout.setf(ios::fixed); // format stałoprzecinkowy
cout << "Obliczanie calki oznaczonej\n"
"za pomoca metody prostokatow\n"
"----------------------------\n"
"(C)2004 mgr J.Walaszek I LO\n\n"
"f(x) = x * x + 2 * x\n\n"
"Podaj poczatek przedzialu calkowania\n\n"
"xp = ";
cin >> xp;
cout << "\nPodaj koniec przedzialu calkowania\n\n"
"xk = ";
cin >> xk;
cout << endl;
s = 0;
dx = (xk - xp) / N;
for(i = 1; i <= N; i++) s += f(xp + i * dx);
s *= dx;
cout << "Wartosc calki wynosi : " << setw(8) << s
<< "\n\nNacisnij klawisz Enter";
cin.getline(c, 1);
cin.getline(c, 1);
} |
Microsoft
Visual
Basic 2005
Express
Edition | '****************************************************
'** Obliczanie całki oznaczonej metodą prostokątów **
'** ---------------------------------------------- **
'** (C)2006 mgr Jerzy Wałaszek I LO w Tarnowie **
'****************************************************
Module Module1
'*******************************
'** Tutaj definiujemy funkcję **
'*******************************
Public Function f(ByVal x As Double) As Double
Return x * x + 2 * x
End Function
'********************
'** Program główny **
'********************
Sub Main()
Const N = 1000 'liczba punktów/prostokątów podziałowych
Dim xp, xk, s, dx As Double
Dim i As Integer
Console.WriteLine("Obliczanie całki oznaczonej")
Console.WriteLine("za pomocą metody prostokątów")
Console.WriteLine("----------------------------")
Console.WriteLine("(C)2006 mgr J.Wałaszek I LO")
Console.WriteLine()
Console.WriteLine("f(x) = x * x + 2 * x")
Console.WriteLine()
Console.WriteLine("Podaj początek przedziału całkowania")
Console.WriteLine()
Console.Write("xp = ") : xp = Val(Console.ReadLine())
Console.WriteLine()
Console.WriteLine("Podaj koniec przedziału całkowania")
Console.WriteLine()
Console.Write("xk = ") : xk = Val(Console.ReadLine())
Console.WriteLine()
s = 0
dx = (xk - xp) / N
For i = 1 To N : s += f(xp + i * dx) : Next
s *= dx
Console.WriteLine("Wartość całki wynosi : {0,8:F3}", s)
' Gotowe
Console.WriteLine()
Console.WriteLine("KONIEC. Naciśnij dowolny klawisz...")
Console.ReadLine()
End Sub
End Module |
| Python | # -*- coding: cp1250 -*-
#****************************************************
#** Obliczanie całki oznaczonej metodą prostokątów **
#** ---------------------------------------------- **
#** (C)2005 mgr Jerzy Wałaszek I LO w Tarnowie **
#****************************************************
#*******************************
#** Tutaj definiujemy funkcję **
#*******************************
def f(x):
return x * x + 2 * x;
#********************
#** Program główny **
#********************
N = 1000 #liczba punktów/prostokątów podziałowych
print "Obliczanie calki oznaczonej"
print "za pomoca metody prostokatów"
print "----------------------------"
print "(C)2005 mgr J.Walaszek I LO"
print
print "f(x) = x * x + 2 * x"
print
print "Podaj poczatek przedzialu calkowania"
print
xp = float(raw_input("xp = "))
print
print "Podaj koniec przedzialu calkowania"
print
xk = float(raw_input("xk = "))
print
s = 0.
dx = (xk - xp) / N
for i in range(1, N + 1):
s += f(xp + i * dx)
s *= dx
print "Wartosc calki wynosi : %8.3f" % s
print
raw_input("Koniec - nacisnij klawisz Enter...") |
| JavaScript | <html>
<head>
<title>Całkowanie numeryczne metodą prostokątów</title>
</head>
<body>
<script language="JavaScript">
//****************************************************
//** Obliczanie całki oznaczonej metodą prostokątów **
//** ---------------------------------------------- **
//** (C)2004 mgr Jerzy Wałaszek I LO w Tarnowie **
//****************************************************
//*******************************
//** Tutaj definiujemy funkcję **
//*******************************
function f(x)
{
return(x * x + 2 * x);
}
function js_rectangle()
{
var N = 1000; //liczba punktów/prostokątów podziałowych
var xp,xk,s,dx,i,t;
xp = parseFloat(document.frm_rectangle.xp_inp.value);
xk = parseFloat(document.frm_rectangle.xk_inp.value);
if(isNaN(xp) || isNaN(xk))
t = "<font color=red><b>Popraw dane wejściowe!</b></font>";
else
{
s = 0;
dx = (xk - xp) / N;
for(i = 1; i <= N; i++) s += f(xp + i * dx);
s *= dx;
t = Math.floor(s * 1000) / 1000;
};
document.getElementById("t_out").innerHTML = t;
}
</script>
<form method="POST"
name="frm_rectangle"
style="border: 2px solid #FF9900;
padding-left: 4px;
padding-right: 4px;
padding-top: 1px;
padding-bottom: 1px;
background-color: #FFFFCC">
<h2 style="text-align: center">
Obliczanie całki oznaczonej<br>
za pomocą metody prostokątów
</h2>
<hr>
<h4 style="text-align: center">
(C)2004 mgr Jerzy Wałaszek I LO w Tarnowie
</h4>
<h3 style="text-align: center">
Całkowana funkcja:
</h3>
<h4 style="text-align: center">
<i>f(x) = x<sup>2</sup> + 2x</i>
</h4>
<p style="text-align: center">
Tutaj określ przedział całkowania
</p>
<p style="text-align: center">
Początek <i>x<sub>p</sub></i> =
<input type="text" name="xp_inp" size="20" value="0">
i koniec <i>x<sub>k</sub> </i>=
<input type="text" name="xk_inp" size="20" value="1">
</p>
<p style="text-align: center">
<input onclick="js_rectangle();" type="button"
value="Oblicz całkę" name="B1">
</p>
<h4 style="text-align: center">
Wartość całki wynosi
</h4>
<p id="t_out" style="text-align: center">...</p>
</form>
</body>
</html> Dokument ten rozpowszechniany jest zgodnie z zasadami licencji
GNU Free Documentation License.
|
Źródło: mgr Jerzy Wałaszek

![]()
2,4142
R
R
N
R
R
N
0
s + f(xp + i
dx)
s
dx