

Aby zrozumieć zasadę metody Monte Carlo wyobraźcie sobie, iż chcecie wyznaczyć pole koła wpisanego w kwadrat o boku równym 2 (pole to co do wartości jest równe liczbie pi, ale na razie udajmy, że o tym nie wiemy). W tym celu wyznaczamy wewnątrz kwadratu dużo losowych punktów. Następnie zliczamy te punkty, które wpadają do wnętrza koła. Pole koła jest w przybliżeniu równe:
| | Pkoło | - pole koła |
| Pkwadrat | - pole kwadratu |
| nkoło | - liczba punktów w kole |
| n | - liczba wszystkich punktów |

Oto odpowiedni skrypt w języku JavaScript, który symuluje obliczanie powierzchni koła dla podanego przykładu:
<html>
<head>
<title>Wyznaczanie liczby PI metodą Monte Carlo</title>
</head>
<body>
<script language="javascript">
//***************************************
//** Przykładowa aplikacja obliczająca **
//** pole koła wpisanego w kwadrat **
//** za pomocą metody Monte Carlo **
//**-----------------------------------**
//** (C)2004 mgr Jerzy Wałaszek I LO **
//***************************************
function js_p()
{
var n = parseInt(document.frm_pi.inp_n.value);
var nk,s,x,y,i;
if(isNaN(n) || (n < 2))
s = "<font color=red><b>Popraw dane</b></font>";
else
{
nk = 0;
for(i = 1; i <= n; i ++)
{
x = Math.random() * 2; y = Math.random() * 2;
if(Math.sqrt((x-1)*(x-1) + (y-1)*(y-1)) <= 1) nk++;
};
s = 4 * nk / n;
s = Math.round(s * 100000) / 100000;
};
document.getElementById("pole").innerHTML = s;
}
</script>
<form method="POST"
name="frm_pi"
style="border: 2px solid #FFCC66;
padding-left: 4px;
padding-right: 4px;
padding-top: 1px;
padding-bottom: 1px;
background-color: #FFFFCC">
<h3 style="text-align: center">
Obliczanie pola koła wpisanego w kwadrat o boku 2<br>
za pomocą metody Monte Carlo
</h3>
<hr>
<p style="text-align: center">
(C)2004 mgr Jerzy Wałaszek I LO w Tarnowie
</p>
<p style="text-align: center">
Podaj liczbę punktów do wygenerowania =
<input type="text" name="inp_n" size="20" value="10000">
</p>
<p style="text-align: center">
<input onclick="js_p();" type="button"
value="Oblicz pole koła" name="B1">
</p>
<p style="text-align: center">
Pole koła wynosi : <span id="pole">...</span>
</p>
</form>
</body>
</html>
Oczywiście wynik jest bliski liczbie π = 3,1415926535... dopiero dla dużych wartości n. Zaczynają wtedy obowiązywać prawa dużych liczb i pomimo przypadkowości wyboru punktów, pojawia się prawidłowość. Ponieważ punkty rozkładają się równomiernie w obrębie pola kwadratu, to stosunek liczby punktów wewnątrz koła do liczby wszystkich punktów w kwadracie jest równy stosunkowi pola koła do pola kwadratu. Stąd właśnie pochodzi nasz wzór:
Wzór ten jest podstawą wyznaczania wartości całki oznaczonej za pomocą metody Monte Carlo, czyli losowania punktów. Zasada jest następująca:
Dla danej funkcji f(x), której całkę oznaczoną chcemy obliczyć w przedziale całkowania <xp,xk>, wyznaczamy prostokąt obejmujący pole pod wykresem tej funkcji o wysokości h i długości podstawy (xk - xp). W dalszej kolejności losujemy n punktów i zliczamy te punkty nw, które wpadają w pole pod wykresem funkcji. Wartość całki wyraża się wzorem przybliżonym:
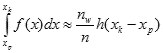
Otrzymany wzór ma kilka wad. Na przykład w ogólnym przypadku trudno wyznaczyć wysokość h. Również kłopoty pojawiają się, gdy funkcja zmienia znak w przedziale całkowania. Dlatego częściej jako metodę Monte Carlo przyjmuje się metodę, która wyznacza średnią z wartości funkcji w przedziale całkowania na podstawie serii losowo wybranych współrzędnych x. Następnie średnia ta jest mnożona przez długość przedziału całkowania i otrzymujemy przybliżoną wartość całki oznaczonej. Wzór ma następującą postać:
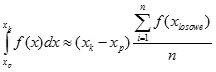
xlosowe jest wartością pseudolosową zmiennoprzecinkową z przedziału <xp, xk> Wartość tę otrzymujemy wg wzorów:
| Język | Instrukcja |
| Pascal | xlosowe := xp + random * (xk - xp); |
| C++ | xlosowe = xp + (double)rand()/(double)(RAND_MAX+1) * (xk - xp); |
| Basic | xlosowe = xp + rnd(1) * (xk - xp) |
| Python | xlosowe = xp + random.uniform(0, dx) |
| JavaScript | xlosowe = xp + Math.random() * (xk - xp) |

Dane wejściowe
| xp | - | początek przedziału całkowania, xp  R R |
| xk | - | koniec przedziału całkowania, xk  R R |
| n | - | liczba punktów losowych, n  N N |
| f(x) | - | funkcja rzeczywista, której całkę liczymy |
Dane wyjściowe
Wartość całki oznaczonej funkcji f(x) w przedziale <xp,xk>. Wynik jest liczbą rzeczywistą.
Zmienne pomocnicze
| s | - | średnia wartość funkcji, s  R R |
| dx | - | długość przedziału całkowania, dx  R R |
| i | - | licznik punktów podziałowych, i  N N |
| xlosowe | - | punkt wybrany losowo z przedziału całkowania, xlosowe  R R |

| krok 1: | Czytaj xp xk n |
| krok 2: | s 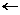 0; dx 0; dx 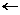 xk - xp xk - xp |
| krok 3: | Dla i = 1,2,...,n, wykonuj kroki 4 i 5. |
| krok 4: | Generuj losową wartość xlosowe w przedziale <xp,xk> |
| krok 5: | s 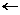 s + f(xlosowe) s + f(xlosowe) |
| krok 6: | s 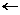 dx dx  | s | | n | |
| krok 7: | Pisz s i zakończ algorytm |

Obliczenia rozpoczynamy od pobrania informacji o przedziale całkowania oraz o ilości punktów losowych, które należy wygenerować w celu obliczenia wartości średniej funkcji w tym przedziale. Dokładność metody rośnie wraz ze wzrostem n.
W zmiennej s będziemy obliczać sumy wartości funkcji. Zmienna ta posłuży później do wyliczenia średniej oraz samej całki oznaczonej. Na początku obliczeń ustawiamy ją na 0. W zmiennej dx zapamiętujemy szerokość przedziału całkowania. Wartość ta jest wykorzystywana zwykle przy generacji liczby losowej oraz na końcu przy obliczeniu wartości całki.
Rozpoczynamy pętlę iteracyjną kontrolowaną przez zmienną i. Pętla ta wykona się n-razy. Wewnątrz pętli generujemy liczbę pseudolosową xlosowe leżącą w przedziale <xp.xk>. Metoda generacji zależy od wybranego języka programowania, który udostępnia odpowiednie funkcje pseudolosowe. Właściwe procedury generacji tej liczby podaliśmy wyżej w tabelce. Po wyznaczeniu liczby pseudolosowej xlosowe obliczamy wartość funkcji w tym punkcie i dodajemy ją do sumy s. Gdy pętla się zakończy, wyliczamy średnią wartość funkcji w przedziale całkowania, mnożymy ją przez długość tego przedziału i otrzymujemy przybliżoną wartość całki oznaczonej. Wypisujemy wyniki i kończymy algorytm.

 | | |
| | |
| | | 
Poniższe, przykładowe programy są praktyczną realizacją omawianego w tym rozdziale algorytmu. Zapewne można je napisać bardziej efektywnie. To już twoje zadanie. Dokładny opis stosowanych środowisk programowania znajdziesz we wstępie. Programy przed opublikowaniem w serwisie edukacyjnym zostały dokładnie przetestowane. Jeśli jednak znajdziesz jakąś usterkę (co zawsze może się zdarzyć), to prześlij o niej informację do autora. Pozwoli to ulepszyć nasze artykuły. Będziemy Ci za to wdzięczni. | |
| | | | |
W przedziale <0,1> całka funkcji f(x) = x2 + 2x ma dokładną wartość 1.333... W naszym programie liczymy n=10000 losowych punktów.
| Wydruk z uruchomionego programu |
Obliczanie całki oznaczonej
Metoda Monte Carlo
----------------------------
(C)2006 mgr J.Wałaszek I LO
f(x) = x * x + 2 * x
Podaj początek przedziału całkowania
xp = 0
Podaj koniec przedziału całkowania
xk = 1
Wartość całki wynosi : 1,337
KONIEC. Naciśnij dowolny klawisz... |
| Microsoft Visual Basic 2005 Express Edition |
Borland
Delphi 7.0
Personal
Edition | //****************************************************
//** Obliczanie całki oznaczonej metodą Monte Carlo **
//** ---------------------------------------------- **
//** (C)2004 mgr Jerzy Wałaszek I LO w Tarnowie **
//****************************************************
program int_montecarlo;
{$APPTYPE CONSOLE}
//*******************************
//** Tutaj definiujemy funkcję **
//*******************************
function f(x : real) : real;
begin
f := x * x + 2 * x;
end;
//********************
//** Program główny **
//********************
const N = 10000; //liczba punktów losowych
var
xp,xk,s,dx : real;
i : integer;
begin
writeln('Obliczanie calki oznaczonej');
writeln(' Metoda Monte Carlo');
writeln('---------------------------');
writeln('(C)2004 mgr J.Walaszek I LO');
writeln;
writeln('f(x) = x * x + 2 * x');
writeln;
writeln('Podaj poczatek przedzialu calkowania');
writeln;
write('xp = '); readln(xp);
writeln;
writeln('Podaj koniec przedzialu calkowania');
writeln;
write('xk = '); readln(xk);
writeln;
randomize; //inicjujemy generator liczb pseudolosowych
s := 0;
dx := xk - xp;
for i := 1 to N do s := s + f(xp + random * dx);
s := dx * s / N;
writeln('Wartosc calki wynosi : ',s:8:3);
writeln;
writeln('Nacisnij klawisz Enter...');
readln;
end. |
Borland
C++ Builder
6.0
Personal
Edition | //****************************************************
//** Obliczanie całki oznaczonej metodą Monte Carlo **
//** ---------------------------------------------- **
//** (C)2004 mgr Jerzy Wałaszek I LO w Tarnowie **
//****************************************************
#include <iomanip>
#include <iostream>
using namespace std;
//*******************************
//** Tutaj definiujemy funkcję **
//*******************************
double f(double x)
{
return(x * x + 2 * x);
}
//********************
//** Program główny **
//********************
main()
{
const int N = 10000; //liczba punktów losowych
double xp,xk,s,dx;
int i;
char c[1];
cout.precision(3); // 3 cyfry po przecinku
cout.setf(ios::fixed); // format stałoprzecinkowy
cout << "Obliczanie calki oznaczonej\n"
" Metoda Monte Carlo\n"
"---------------------------\n"
"(C)2004 mgr J.Walaszek I LO\n\n"
"f(x) = x * x + 2 * x\n\n"
"Podaj poczatek przedzialu calkowania\n\n"
"xp = ";
cin >> xp;
cout << "\nPodaj koniec przedzialu calkowania\n\n"
"xk = ";
cin >> xk;
cout << endl;
srand((unsigned)time(NULL));
s = 0;
dx = xk - xp;
for(i = 1; i <= N; i++)
s += f(xp+((double)rand()/(double)(RAND_MAX+1)*dx));
s = dx * s / N;
cout << "Wartosc calki wynosi : " << setw(8) << s
<< "\n\nNacisnij klawisz Enter";
cin.getline(c, 1);
cin.getline(c, 1);
} |
Microsoft
Visual
Basic 2005
Express
Edition | '****************************************************
'** Obliczanie całki oznaczonej metodą Monte Carlo **
'** ---------------------------------------------- **
'** (C)2006 mgr Jerzy Wałaszek I LO w Tarnowie **
'****************************************************
Module Module1
'*******************************
'** Tutaj definiujemy funkcję **
'*******************************
Public Function f(ByVal x As Double) As Double
Return x * x + 2 * x
End Function
'********************
'** Program główny **
'********************
Sub Main()
Const N = 10000 'liczba punktów losowych
Dim xp, xk, s, dx As Double
Dim i As Integer
Console.WriteLine("Obliczanie całki oznaczonej")
Console.WriteLine(" Metoda Monte Carlo")
Console.WriteLine("----------------------------")
Console.WriteLine("(C)2006 mgr J.Wałaszek I LO")
Console.WriteLine()
Console.WriteLine("f(x) = x * x + 2 * x")
Console.WriteLine()
Console.WriteLine("Podaj początek przedziału całkowania")
Console.WriteLine()
Console.Write("xp = ") : xp = Val(Console.ReadLine())
Console.WriteLine()
Console.WriteLine("Podaj koniec przedziału całkowania")
Console.WriteLine()
Console.Write("xk = ") : xk = Val(Console.ReadLine())
Console.WriteLine()
Randomize()
s = 0
dx = xk - xp
For i = 1 To N : s += f(xp + Rnd() * dx) : Next
s *= dx / N
Console.WriteLine("Wartość całki wynosi : {0,8:F3}", s)
' Gotowe
Console.WriteLine()
Console.WriteLine("KONIEC. Naciśnij dowolny klawisz...")
Console.ReadLine()
End Sub
End Module |
| Python | # -*- coding: cp1250 -*-
#****************************************************
#** Obliczanie całki oznaczonej metodą Monte Carlo **
#** ---------------------------------------------- **
#** (C)2005 mgr Jerzy Wałaszek I LO w Tarnowie **
#****************************************************
import random
#*******************************
#** Tutaj definiujemy funkcję **
#*******************************
def f(x):
return x * x + 2 * x;
#********************
#** Program główny **
#********************
N = 10000 #liczba punktów losowych
print " Obliczanie calki oznaczonej"
print " za pomoca metody Monte Carlo"
print "-----------------------------"
print "(C)2005 mgr J.Walaszek I LO"
print
print "f(x) = x * x + 2 * x"
print
print "Podaj poczatek przedzialu calkowania"
print
xp = float(raw_input("xp = "))
print
print "Podaj koniec przedzialu calkowania"
print
xk = float(raw_input("xk = "))
print
s = 0.
dx = xk - xp
for i in range(N):
s += f(xp + random.uniform(0, dx))
s *= dx / N
print "Wartosc calki wynosi : %8.3f" % s
print
raw_input("Koniec - nacisnij klawisz Enter...") |
| JavaScript | <html>
<head>
<title>Całkowanie numeryczne metodą Monte Carlo</title>
</head>
<body>
<script language="JavaScript">
//****************************************************
//** Obliczanie całki oznaczonej metodą Monte Carlo **
//** ---------------------------------------------- **
//** (C)2004 mgr Jerzy Wałaszek I LO w Tarnowie **
//****************************************************
//*******************************
//** Tutaj definiujemy funkcję **
//*******************************
function f(x)
{
return(x * x + 2 * x);
}
function js_simpson()
{
var N = 10000; //liczba punktów losowych
var xp,xk,s,dx,i,t;
xp = parseFloat(document.frm_montecarlo.xp_inp.value);
xk = parseFloat(document.frm_montecarlo.xk_inp.value);
if(isNaN(xp) || isNaN(xk))
t = "<font color=red><b>Popraw dane wejściowe!</b></font>";
else
{
s = 0;
dx = xk - xp;
for(i = 1; i <= N; i++) s += f(xp + Math.random() * dx);
s = dx * s / N;
t = Math.floor(s * 1000) / 1000;
};
document.getElementById("t_out").innerHTML = t;
}
</script>
<form method="POST"
name="frm_montecarlo"
style="border: 2px solid #FF9900;
padding-left: 4px;
padding-right: 4px;
padding-top: 1px;
padding-bottom: 1px;
background-color: #FFFFCC">
<h2 style="text-align: center">
Obliczanie całki oznaczonej<br>
za pomocą metody Monte Carlo
</h2>
<hr>
<h4 style="text-align: center">
(C)2004 mgr Jerzy Wałaszek I LO w Tarnowie
</h4>
<h3 style="text-align: center">
Całkowana funkcja:
</h3>
<h4 style="text-align: center">
<i>f(x) = x<sup>2</sup> + 2x</i>
</h4>
<p style="text-align: center">
Tutaj określ przedział całkowania
</p>
<p style="text-align: center">
Początek <i>x<sub>p</sub></i> =
<input type="text" name="xp_inp" size="20" value="0">
i koniec <i>x<sub>k</sub> </i>=
<input type="text" name="xk_inp" size="20" value="1">
</p>
<p style="text-align: center">
<input onclick="js_montecarlo();" type="button"
value="Oblicz całkę" name="B1">
</p>
<h4 style="text-align: center">
Wartość całki wynosi
</h4>
<p id="t_out" style="text-align: center">...</p>
</form>
</body></html>
Dokument ten rozpowszechniany jest zgodnie z zasadami licencji
GNU Free Documentation License.
|
Źródło: mgr Jerzy Wałaszek

![]()
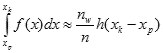
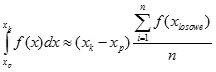
R
R
N
R
R
N
R
0; dx
xk - xp
s + f(xlosowe)
dx

